Campo magnético y flujo magnético
Como ya sabemos, los fenómenos magnéticos pueden describirse mediante un campo dependiente del tiempo y extendido en el espacio. Denotaremos este campo con la letra B.
Como el campo está extendido en el espacio, en realidad podemos limitarnos a una superficie determinada y considerar únicamente el efecto del campo magnético. Como veremos en el apartado siguiente, la ley de Faraday se refiere a los flujos magnéticos, por lo que ahora presentamos su definición para el caso de un campo magnético uniforme.
El flujo magnético es la cantidad de campo magnético que atraviesa perpendicularmente una determinada superficie.
El flujo magnético puede calcularse de la siguiente manera:
\[\Phi = \vec{B} \cdot \vec{A} = |\vec{B}| \cdot |\vec{A}| \cdot \cos(\theta)\].
Aquí, el punto indica un producto escalar y el vector A lleva el valor de una determinada superficie y está dirigido en la dirección del vector normal de la superficie. El símbolo | | indica el módulo del vector y θ representa el ángulo entre el vector normal y el vector del campo magnético. Mira la imagen siguiente para aclararlo:
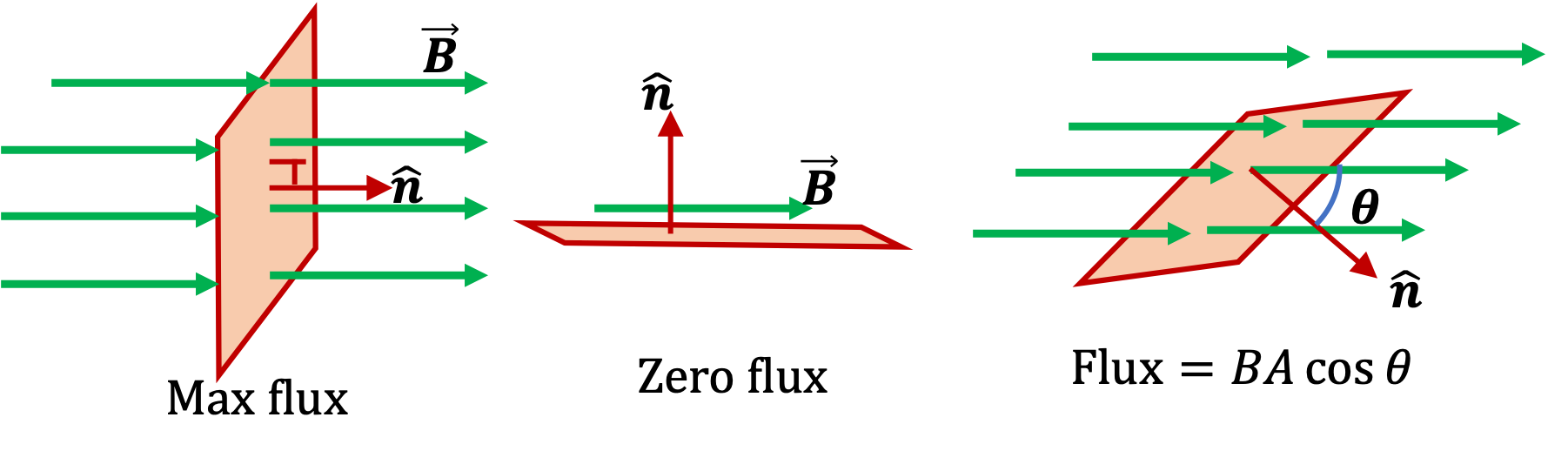
Flujo magnético dependiente de la orientación a través de una superficie plana. www.physicsbootcamp.org
En entornos complejos, el campo magnético no es uniforme y la superficie no es plana (lo que conduce al uso de integrales y caracterizaciones que están fuera del alcance de este artículo). Sólo consideraremos superficies planas y campos magnéticos uniformes. Esto dará lugar a una dependencia del flujo magnético del ángulo entre el campo magnético y la superficie.
Ley de Faraday
La ley de Faraday es una ley experimental que más tarde se formalizó matemáticamente y se incorporó como parte de lo que hoy conocemos como leyes de Maxwell. Relaciona un concepto del campo eléctrico, la diferencia de potencial, con el flujo magnético.
En concreto, relaciona la fuerza electromotriz (FEM) con la velocidad de cambio del flujo magnético. La fuerza electromotriz es la energía necesaria por unidad de carga para establecer una determinada diferencia de potencial eléctrico entre dos puntos y se suele denotar con la letra ε.
La descripción matemática de la ley de Faraday es:
\[\varepsilon = - \frac{d \phi}{dt}\]
donde hay una derivación respecto al tiempo del flujo. Aunque esta descripción es muy general, si nos limitamos al caso antes mencionado de campo magnético uniforme y un área fija, llegamos, debido a la expresión del producto escalar, a la siguiente ecuación
\[\varepsilon = \omega \cdot |||vec{B}| \cdot |||vec{A}| \cdot \sin(\theta)\].
donde ω es la velocidad angular del ángulo cambiante. La imagen siguiente es un montaje experimental para producir una fuerza electromotriz utilizando una determinada superficie móvil y un campo magnético uniforme.
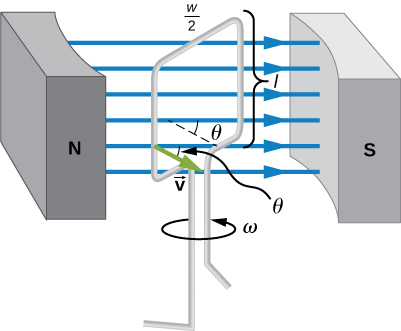
Montaje experimental para la ley de Faraday. openpress.usask.ca
¿Qué es el enlace de flujo magnético?
Las ecuaciones que rigen el comportamiento del campo electromagnético (leyes de Maxwell) son lineales, lo que significa que podemos considerar la superposición de diferentes campos que cumplan las mismas ecuaciones. Si consideramos un montaje experimental que genera una fuerza electromotriz, una cantidad sencilla puede ayudar a aumentar la producción de fuerza electromotriz; es lo que llamamos enlace. La vinculación del flujo magnético se mide en unidades de Webers \(\mathrm{Wb}\) al igual que el flujo magnético.
Configuración experimental de la vinculación del flujo magnético
Imagina el escenario que teníamos antes: una bobina que gira en presencia de un campo magnético. La variación del flujo magnético induce una fuerza electromotriz. Si ahora tomamos el mismo escenario con N bobinas, podemos crear N superficies diferentes, de modo que la fuerza electromotriz se multiplica por un factor N. Esto es lo que llamamos enlace de flujo.
Descripción matemática del acoplamiento de flujo magnético
La descripción matemática del acoplamiento de flujo se basa en la ley de Faraday. De nuevo, como estamos considerando configuraciones sencillas, nos limitaremos al caso en el que tenemos N bobinas idénticas y este número permanece constante. Además, todas están sincronizadas y tienen la misma orientación tridimensional. Esto conduce al siguiente aumento del flujo
\[\phi_L = N \cdot \phi \Derecha \varepsilon_L = N \cdot \varepsilon\].
donde ϕL es el enlace de flujo magnético total resultante de N bobinas y εL es la fuerza electromotriz total asociada. Combinando esto con la ley de Faraday obtenemos la ecuación del enlace de flujo magnético\[\phi_L=N\cdot|B|\cdot|A|\cdot\sin\left(\theta\right)\].
Haciendo esto, podemos conseguir aumentar la diferencia de potencial con una simple adición de bobinas similares que podemos conectar a la misma configuración del circuito.
A continuación vamos a considerar varios ejemplos de montajes experimentales. El campo magnético presente tiene un valor de 10 Teslas, mientras que el área de las bobinas que estamos utilizando es de 1m2. Hacemos girar la bobina con una velocidad angular de 2 rad/s.
Imagina que el campo magnético está dirigido en el eje x, es decir
\(\vec{B} = (10,0,0)T\)
Por otro lado, el vector normal evoluciona de la siguiente manera
\(\vec{A} = (\cos(2 \cdot t), \sin(2 \cdot t), 0) m^2\)
donde t es el tiempo. Esto da la siguiente expresión para el flujo magnético:
\(\phi = \vec{B} \cdot \vec{A} = 10 \cdot \cos(2 \cdot t) Wb\)
Esto nos permite calcular fácilmente
\(10 \cdot \cos(2 \cdot t)) = 20 \cdot \sin(2 \cdot t) V\)
A continuación encontrarás un gráfico que muestra la evolución temporal del flujo magnético y de la fuerza electromotriz generada.
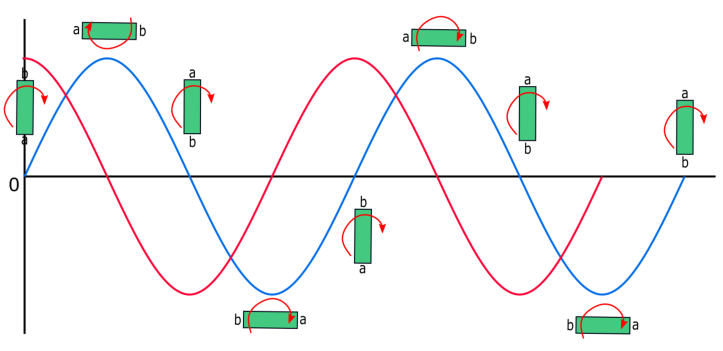
Evolución temporal del flujo magnético (rojo) y de la fuerza electromotriz (azul).
Si hubiéramos conseguido aumentar el campo magnético o hacer más grande la superficie de la bobina, también podríamos haber generado una fuerza electromotriz, ya que estamos variando el flujo magnético en el tiempo.
Si ahora consideramos 20 bobinas idénticas girando sincrónicamente, el gráfico de la dependencia temporal de la densidad de flujo magnético y la fuerza electromotriz tendría este aspecto:
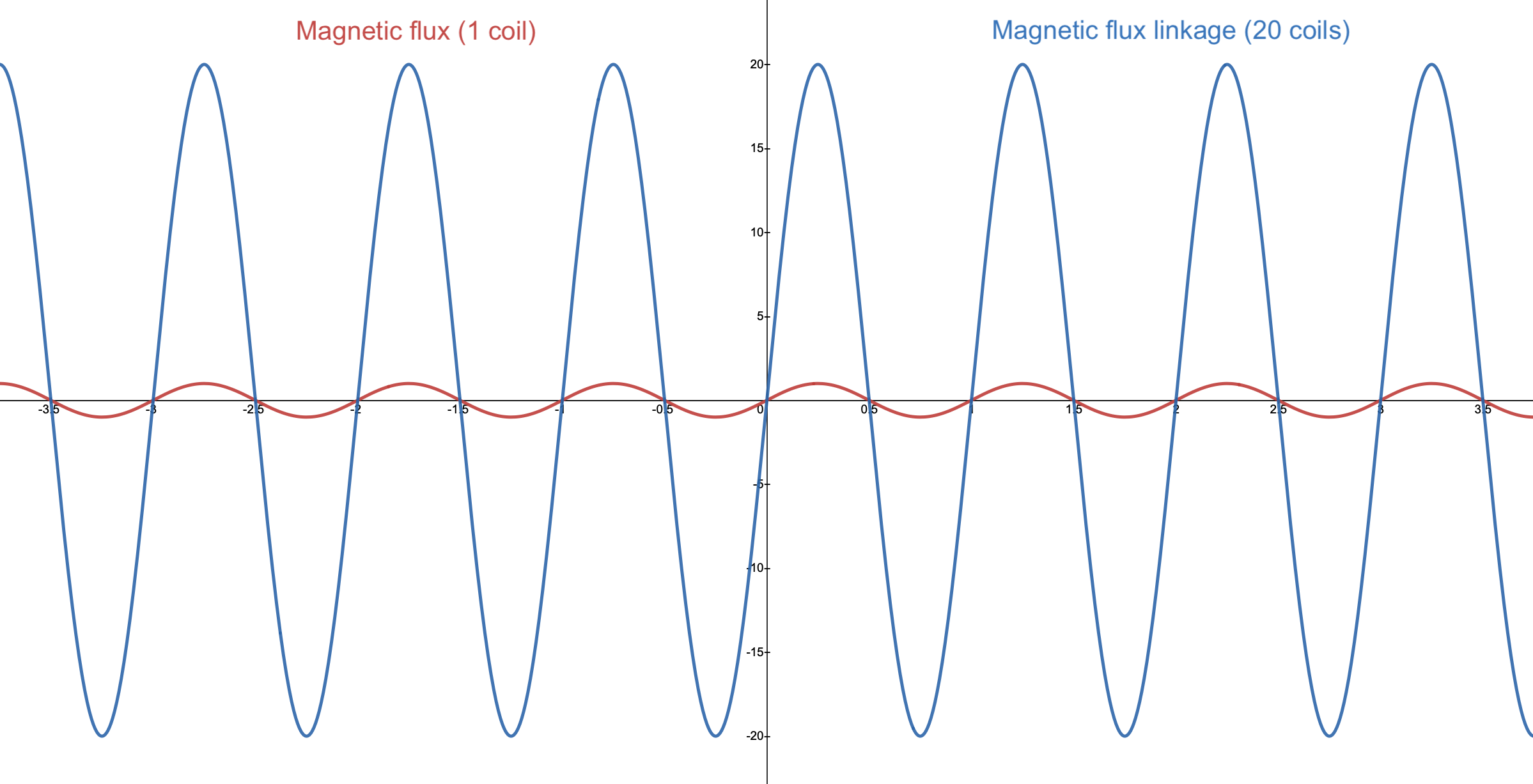
Comparación entre un montaje con 1 bobina y con 20 bobinas. En el eje horizontal se representa el tiempo y en el vertical la fuerza electromotriz
Vemos aquí que los valores del flujo total (y, por tanto, de la FEM) han crecido significativamente al utilizar sólo 19 bobinas adicionales.
Pasemos ahora brevemente al caso de una superficie estática y un campo magnético variable. Si ahora el campo comienza con un valor inicial de 0 Teslas, pero sigue creciendo con el tiempo de la siguiente manera
\(\vec{B} = (10 \cdot t, 0,0) T\)
Considera una superficie cuyo vector normal es
\(\vec{A} = (1,0,0)m^2\)
Llegaremos a la siguiente expresión para el flujo magnético
\(\phi = \vec{B} \cdot \vec{A} = 10 \cdot t \space Wb\)
La derivada temporal de esta expresión da la expresión de la fuerza electromotriz, es decir
\(\varepsilon = -\frac{d \phi}{dt} = - \frac{d}{dt}(10 \cdot t) = -10 \space V\)
Generaría una fuerza electromotriz constante entre los puntos extremos de la bobina. Por supuesto, podríamos utilizar varias bobinas para construir un enlace de flujo magnético y aumentar la potencia.
De hecho, cuando utilizamos varias bobinas, lo habitual es variar el campo magnético y no la orientación para generar una fuerza electromotriz. Ésta es la razón por la que solemos asociar el concepto de flujo magnético y la ley de Faraday a una sola bobina giratoria, mientras que el concepto de enlace de flujo suele designar varias bobinas estáticas en presencia de un campo magnético.
Flujo magnético y enlace de flujo magnético - Puntos clave
- El flujo magnético es una magnitud que mide la cantidad de campo magnético que atraviesa perpendicularmente una determinada superficie.
- La ley de Faraday establece una relación entre una fuerza que crea una diferencia de potencial electromagnético y la variación del flujo magnético en el tiempo.
- La ley de Faraday se aplica siempre que al menos uno de estos tres factores varíe con el tiempo: la intensidad del campo magnético, la superficie que atraviesa o la orientación de la superficie respecto al campo.
- La situación en la que hay varias bobinas por las que pasa un campo magnético se denomina enlace de flujo. El flujo aumenta proporcionalmente.











