¿Cuáles son las leyes de conservación de las partículas?
La idea es que cualquier interacción de partículas no debe cambiar la energía total, la masa total y la carga total de las partículas. La propiedad que describe este intercambio de energía y masa se denomina leyes de conservación, también conocidas como "leyes de conservación de la física de partículas" o "leyes de conservación en física nuclear". Son las siguientes
- Conservaciónde la masa y la energía: la masa y la energía de las partículas antes y después del intercambio deben ser iguales.
- Conservacióndel momento: la velocidad multiplicada por la masa de las partículas antes y después del intercambio debe ser la misma. Si el producto de la masa por la velocidad es el momento, podemos reformularlo como que el momento total de las partículas del sistema antes y después del impacto es el mismo.
- Conservación del número debariones: el número total de bariones de las partículas antes y después del intercambio es el mismo.
- Conservación del número deleptones: el número total de leptones de las partículas antes y después del intercambio es el mismo.
- Conservación dela carga: la carga total de las partículas antes y después del intercambio es la misma.
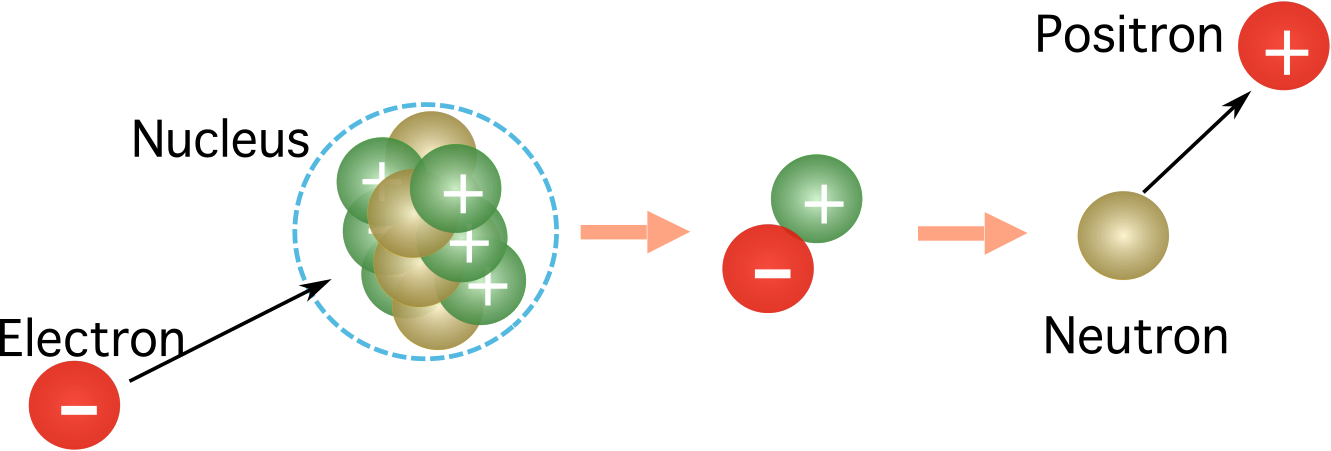
Figura 1. Captura de un electrón por el núcleo. Mientras que la carga del electrón anula la carga del protón, la carga positiva se libera en forma de positrón. La masa se conserva, ya que el neutrón tiene una masa igual a la del protón, y el positrón tiene la misma masa que el electrón. Fuente: Manuel R. Camacho, StudySmarter.
Conservación en las reacciones nucleares de protón a neutrón
Consideremos un ejemplo de conservación de la carga elemental y del número de bariones y leptones en un proceso de interacción débil (en el que interviene la fuerza nuclear débil).
En física nuclear, para que un protón se convierta en neutrón, debe perder su carga manteniendo su número de bariones. El proceso de conversión de protón en neutrón es
\[^1_1{p} \rightarrow ^1_0{n}\]
El protón debe perder su carga positiva. Sin embargo, la ley de conservación establece que la carga total antes y después de la conversión debe ser la misma.
\[\text{Carga total inicial = Carga total final}\]
En este caso, la carga total del protón es 1, mientras que la carga total del neutrón es 0.
\[^{qquad \qquad 1}_{carga = 1}{p} \carga = 0} {n}].
Los protones están formados por dos partículas hacia arriba y una hacia abajo, con cargas de +⅔ y -⅓. El neutrón, en cambio, está formado por dos partículas hacia abajo y una hacia arriba.
\[p = (udu) = \Big(\frac{2}{3} - \frac{1}{3} + \frac{2}{3} \Big) = 1\].
\[n = (dud) = \Big( -\frac{1}{3} +\frac{2}{3} -\frac{1}{3} \Big) = 0\].
Por tanto, el protón debe perder 3⁄3 de la carga. La partícula que debe cambiar es uno de los quarks up del protón, por lo que las cargas se anulan entre sí: u → d = ⅔ → -⅓. La suma para el protón será ⅔-⅓-⅓ = 0.
La única forma de conseguirlo es liberando una carga de 1. Por tanto, hay que liberar una partícula. En este caso, el protón emite un positrón.
\π[^{qquad \qquad 1}_{carga = 1}{p} \^{qquad 1}_carga = 0}{n} + ^{qquad 1}_carga = 0}{n} + ^{qquad \quad 0}_carga= 1}{e}^+]
Ahora las cargas están equilibradas y se conservan. Antes del proceso, teníamos una carga de 1, y después, seguimos teniendo una carga de 1.
El positrón tiene un número de bariones cero, mientras que el protón y el neutrón tienen un número de bariones uno, conservándose así el número de bariones.
\[\text{número bariónico inicial = número bariónico final}]
\[_{texto{número de bariones = 1}}{p} \^{texto}{Número de bariones = 1}}{n}. + _{\text{número de bariones = 0}}{e}^+]
El electrón es un leptón. Cada leptón tiene un número leptónico, como se indica en la tabla siguiente.
| Tabla 1. Leptones |
|---|
| Partícula | Carga eléctrica | Número de leptones | Antipartícula | Carga eléctrica | Número de leptones |
| Electrón | -1 | 1 | Positrón | 1 | -1 |
| Electrón neutrino | 0 | 1 | Neutrino antielectrón | 0 | -1 |
| Muón | -1 | 1 | Antimuón | 1 | -1 |
| Muón neutrino | 0 | 1 | Neutrino antimuón | 0 | -1 |
| Tau | -1 | 1 | Anti-Tau | 1 | -1 |
| Neutrino tau | 0 | 1 | Neutrino anti-Tau | 0 | -1 |
En la fórmula de la reacción protón-neutrón hay una anomalía. El protón y el neutrón tienen cada uno un número leptónico de 0, pero el positrón tiene un número leptónico de -1.
\[(\text{número de leptones} = 0)p \rightarrow (\text{número de leptones}= 0)n + (\text{número de leptones} = -1)e^+\].
Para equilibrar el número leptónico, necesitamos añadir otra partícula con un número leptónico de 1 y una carga de 0. La partícula que hay que añadir es un neutrino electrónico vε
\(p \\\nrightarrow n + e^+ + v_{\varepsilon}\)
Esto puede resumirse como sigue
\(^1_1p \rightarrow ^1_0n + ^0_1e^+ +v_{\\varepsilon}\)
En esta reacción, el número de bariones se conserva, la carga se conserva y el número de leptones también se conserva.
La reacción de protón a neutrón también puede resumirse como la transformación de uno de los quarks up del protón en un quark down, un positrón y un neutrino.
\(u \rightarrow d + e^+ + v_{\varepsilon}\)
He aquí la reacción representada por un diagrama de Feynman:
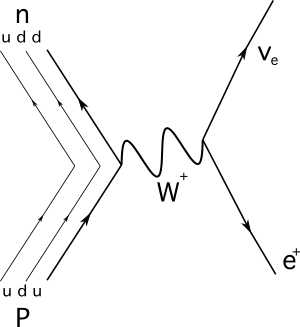
Figura 2. Desintegración de protón en neutrón. Fuente: Manuel R. Camacho, StudySmarter.
La partícula que actúa como mediadora en esta reacción es un bosón W plus.
Conservación en los intercambios de energía y momento
Las partículas conservan tanto su momento como su energía en la mecánica cuántica, como se observó en los primeros experimentos con rayos X. El físico estadounidense Arthur Compton observó estos efectos como una disminución de la longitud de onda y una dispersión de los fotones. Teorizó que la disminución de la longitud de onda y la dispersión estaban causadas por los electrones del material. Las colisiones hacen que los fotones se dispersen en ángulo y reduzcan su energía cediéndola a los electrones, efecto que se conoce como efecto Compton. Pon el siguiente ejemplo.
Un fotón con una longitud de onda de 0,03 nm impacta en un electrón y cambia su longitud de onda a 1 nm. ¿Cuánta energía ha recibido el electrón si éste tenía una energía inicial de Ei?
La energía de un fotón se calcula mediante la siguiente ecuación energía-fotón:
\(E = h \cdot f\)
Aquí, f es la frecuencia medida en hercios, mientras que h es la constante de Planck con un valor de 6,63⋅10-34m2⋅kg/s. Necesitamos hallar la frecuencia de una longitud de onda dada, utilizando la fórmula siguiente, donde c es la velocidad de la luz en metros por segundo.
\(f = \frac{c}{\lambda}\)
La energía dada al electrón será igual a la diferencia de las energías antes y después de la colisión o ΔE = Ei -Ef. La contracción de la longitud de onda fue igual a 0,07 nm, como puedes ver a continuación.
\(\Delta E = E_i - E_f = \frac{h \cdot c}{\lambda_i - \lambda_f}\)
\(E = h \cdot \frac{c}{\delta \lambda} = \frac{(6,63 \cdot 10^{-34} m^2 \space kg/s) \cdot (3 \cdot 10^8 m/s)}{(0,07 \cdot 10^{-9} m)} = 2,8 \cdot 10^{-15} julios\)
La energía transferida al electrón con una energía inicial de Ei es
\(E_{Electrón} = E_i+ E = E_i + (2,8 \cdot 10^{-15}) Julios\)
El efecto Compton es importante porque proporciona información sobre el momento de un fotón, que viene dado como la constante de Planck dividida por la longitud de onda del fotón:
El efecto Compton era importante porque proporcionaba información sobre el momento de un fotón, donde el momento venía dado como la constante de Planck dividida por la longitud de onda del fotón, como se indica a continuación.
\(\text{momento fotónico} = \frac{h}{\lambda})
Leyes de conservación - Puntos clave
- Las partículas obedecen las leyes de conservación.
- Las leyes de conservación establecen que la energía, la masa, el momento y el número de las partículas deben conservarse.
- Para que la conservación sea posible, las partículas deben liberar energía u otras partículas que equilibren sus números y propiedades.









