Definición del área entre dos curvas
El área entre dos curvas se define como sigue:
Para dos funciones, \(f(x)\) y \(g(x)\), si \(f(x) \geq g(x)\) para todos los valores de x en el intervalo \([a, \ b]\), entonces el área entre estas dos funciones es igual a la integral de \(f(x) - g(x)\);
Hasta ahora se ha hablado del área con respecto al eje \(x\)-. ¿Y si en lugar de eso te piden que calcules el área con respecto al eje \(y)? En este caso, la definición cambia ligeramente:
Para dos funciones, \(g(y)\) y \(h(y)\), si \(g(y) \geq f(x)\) para todos los valores de \(y\) en el intervalo \([c, d]\), entonces el área entre estas funciones es igual a la integral de \(g(y) -h(y)\).
Fórmula del área entre dos curvas
Por la definición del área entre dos curvas, sabes que el área es igual a la integral de \(f(x)\) menos la integral de \(g(x)\), si \(f(x) \geq g(x)\) sobre el intervalo \([a,b]\). Por tanto, la fórmula utilizada para calcular el área entre dos curvas es la siguiente
\[\begin{align} \text{Área } = & \int^b_a f(x) dx - \int^b_a g(x) \, \mathrm{d}x \\end{align}\]
Esto puede simplificarse para darnos la fórmula final del área:
\[\text{Área } = \int^b_a \left ( f(x) - g(x) \right ) \, \mathrm{d}x\]
La figura 1 ilustra la lógica de esta fórmula.
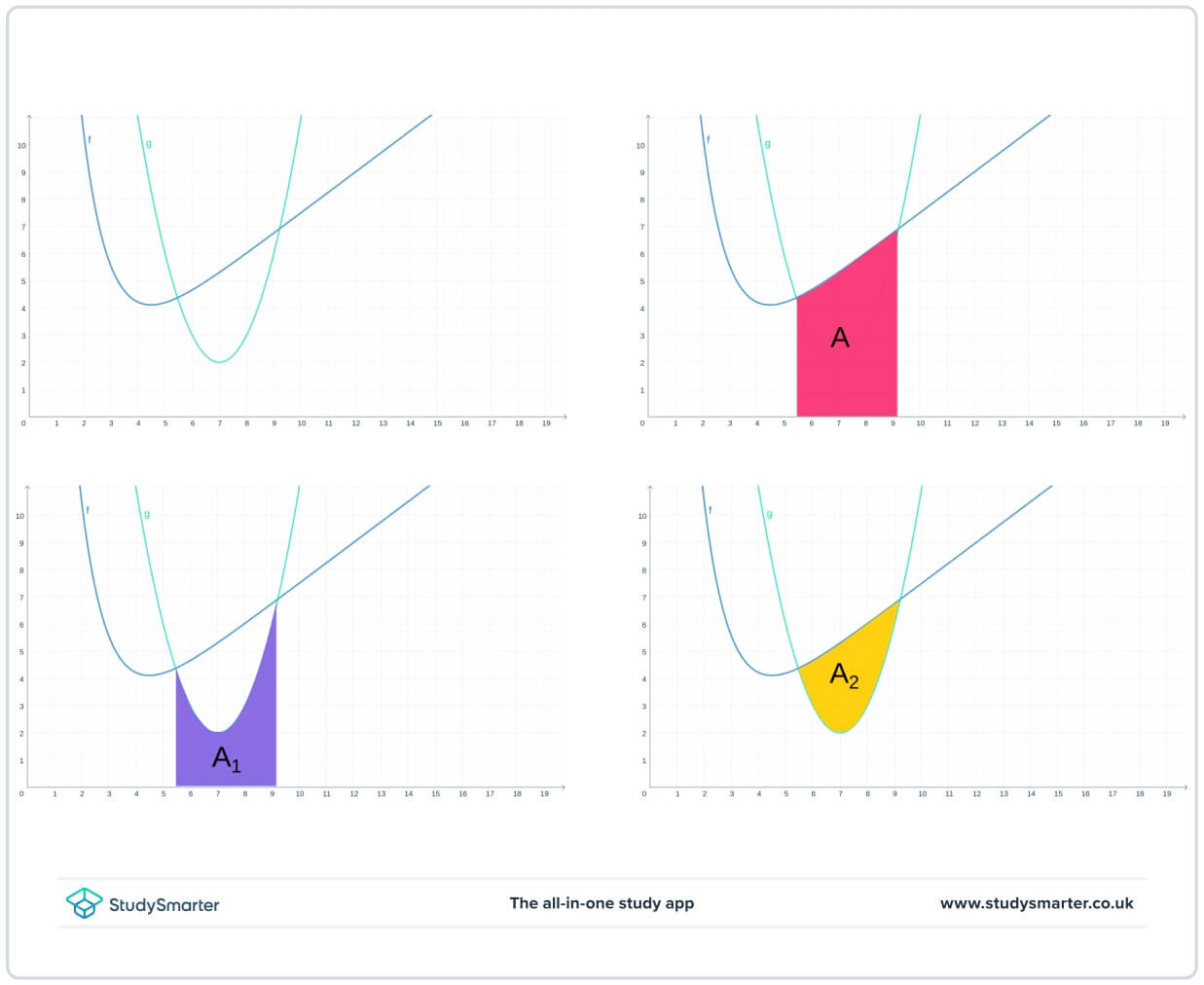
Figura. 1- Cálculo del área entre dos curvas restando el área bajo una curva de la otra. Aquí el área bajo \(g(x)=A_1\) se resta del área bajo \(f(x)=A\), el resultado es \(A_2\)
Puede resultar confuso recordar qué gráfica debe restarse de cuál. Sabes que \(f(x)\) debe ser mayor que \(g(x)\) en todo el intervalo y, en la figura anterior, puedes ver que la gráfica de \(f(x)\) está por encima de la gráfica de \(g(x)\) en todo el intervalo. Por tanto, puede decirse que el área entre dos curvas es igual a la integral de la ecuación de la gráfica superior menos la gráfica inferior, o en forma matemática \[ Área = \int_a^b( y_{texto{superior}} - y_{texto{inferior}}) \, \mathrm{d}x \].
Fórmula del área entre dos curvas - eje y
La fórmula utilizada para calcular el área entre dos curvas con respecto al eje \(y\) es muy similar a la utilizada para calcular el área entre dos curvas con respecto al eje \(x\). La fórmula es la siguiente
\[\begin{align}\text{Área} = & \int^d_c g(y) \; dy - \int^d_c h(y) \, \mathrm{d}y \= & \int^d_c (g(y) - h(y) ) \, \mathrm{d}y\end{align}\]
donde \(g(y) \geq h(y) \) para todos los valores de \(y\) en el intervalo \([c, d]\).
Como \(g(y)\) debe ser mayor que \(h(y)\) en todo el intervalo \([c.d]\), también puedes decir que el área entre dos curvas con respecto al eje \(y)-es igual a la integral de la gráfica de la derecha menos la gráfica de la izquierda, o en forma matemática:
\[\text{Area} = \int_c^d \left (x_{\text{right}} - x_{\text{left}} \right) \, \mathrm{d}y\]
Algo que debes tener en cuenta al integrar con respecto al eje \(y\) son las áreas con signo. Las regiones a la derecha del eje \(y) tendrán un área con signo positivo, y las regiones a la izquierda del eje \(y) tendrán un área con signo negativo .
Considera la función \(x = g(y)\). La integral de esta función es el área con signo entre la gráfica y el eje \(y)\ para \(y \en [c,d]\). El valor de esta área con signo es igual al valor del área a la derecha del eje \(y\)- menos el valor del área a la izquierda del eje \(y\)-. La figura siguiente ilustra el área con signo de la función \(x = \frac{1}{4}y^2 -4\).
 Figura. 2 - Área con signo de la función \(x = \frac{1}{4}y^2 - 4\)
Figura. 2 - Área con signo de la función \(x = \frac{1}{4}y^2 - 4\)
Recuerda que el área a la izquierda del eje \(y\) es negativa, por lo que al restar esa área del área a la derecha del eje \(y\), acabas sumándola.
Pasos para calcular el área entre dos curvas
Hay una serie de pasos que puedes seguir para que el cálculo del área entre dos curvas sea relativamente indoloro.
Paso 1: Determina qué función está encima. Esto se puede hacer esbozando las funciones o, en los casos de funciones cuadráticas, completando el cuadrado. Los esbozos no sólo te ayudarán a determinar qué gráfica, sino que también te ayudarán a ver si hay interceptos entre las gráficas que debas tener en cuenta.
Paso 2: Establece las integrales. Puede que tengas que manipular la fórmula o dividir las funciones en distintos intervalos que queden dentro del original, dependiendo de las intersecciones y del intervalo sobre el que debas calcular el intercepto.
Paso 3: Evalúa las integrales para obtener el área.
En el siguiente apartado se muestra cómo puedes poner en práctica estos pasos.
Ejemplos de área entre dos curvas
Halla el área limitada por las gráficas \(f(x) = x + 5\) y \(g(x) = 1\) sobre el intervalo \([1, 5]\).
Solución:
Paso 1: Determina qué función está encima.
 Figura. 3 - Gráficas de \(f(x) = x+5\) y \(g(x) = 1\)
Figura. 3 - Gráficas de \(f(x) = x+5\) y \(g(x) = 1\)
De la Figura 3 se deduce claramente que \(f(x)\) es la gráfica superior.
Es útil sombrear la región para la que estás calculando el área, para evitar confusiones y posibles errores.
Paso 2: Establece las integrales. Has determinado que \(f(x)\) está por encima de \(g(x)\), y sabes que el intervalo es \([1,5]\). Ahora puedes empezar a sustituir estos valores en la integral.
\[\begin{align}\text{Área} & = \int_{1}^{5} (f(x) - g(x)) \& = \int_{1}^{5} (x + 5 - 1) \, \mathrm{d}x \& = \int_{1}^{5} (x + 4) \, \mathrm{d}x \\end{align}\]
Paso 3: Evalúa la integral.
\[\begin{align}\text{Área} & = \int_{1}^{5} (x + 5), \mathrm{d}x \& = \left. \left (\frac{1}{2}x^2 + 5x \right) \right |_1^5 \\\& = 28\end{align}\]
¿Cómo calcularías el área entre dos curvas si no se da ningún intervalo? En el siguiente ejemplo se detalla cómo hacerlo:
Calcula el área encerrada por las gráficas de \(f(x) = -x^2 + 4x \) y \(g(x) = x^2\).
Solución:
Paso 1: Determina qué gráfica está arriba. También debes determinar el intervalo, ya que no se ha dado ninguno.
 Figura. 4 - Gráficas de \(f(x) = -x^2 + 4x\) y \(g(x) = x^2\)
Figura. 4 - Gráficas de \(f(x) = -x^2 + 4x\) y \(g(x) = x^2\)
En el esquema puedes ver que se delimita un área cuando la gráfica de \(f(x)\) está por encima de \(g(x)\). Por tanto, el intervalo deben ser los valores de \(x) para los que \(f(x) \geq g(x)\). Para determinar este intervalo, debes encontrar los valores \(x\) para los que \(f(x) = g(x)\).
\[\begin{align}f(x) & = g(x) \-x^2 + 4x & = x^2 \2x^2 - 4x & = 0 \x(x - 2) & = 0 \ \qquad x = 0 &\text{ y } x = 2\end{align}\]
Paso 2: Establece las integrales. El área delimitada por las gráficas estará sobre el intervalo \([0,2]\).
\[\begin{align}\text{Área} & = \int_0^2 \left( f(x) - g(x) \right) \, \mathrm{d}x \& = \int_0^2 \left( -x^2 + 4x - x^2 \right) \, \mathrm{d}x \& = \int_0^2 \left( -2x^2 +4x \right) \, \mathrm{d}x \\\\end{align}\]
PASO 3: Evalúa las integrales.
\[\begin{align}\text{Área} & = \int_0^2 \left( -2x^2 + 4x \right ) \, \mathrm{d}x \& = \left. \left(-\frac{2}{3} x^3 + 2x^2 \right) \right |_0^2 \\& = \frac{8}{3}\end{align}\]
Este ejemplo es otro en el que intervienen dos parábolas, pero en este caso no se intersecan, y el intervalo está dado.
Halla el área de la región comprendida entre las gráficas de \(f(x) = -(x-6)^2 + 4\) y \(g(x) = (x-5)^2 + 7\) sobre el intervalo \([4,7]\).
Solución:
Paso 1: Determina la gráfica superior. Ambas funciones son parábolas, por lo que puedes completar el cuadrado para determinar cuál se encuentra arriba. En este ejemplo, ya se te han dado en forma de cuadrado completado.
La gráfica de \(f(x)\) es una parábola descendente con su punto de inflexión en \((6,4)\). La gráfica de \(g(x)\) es una parábola invertida cuyo punto de inflexión está en \((5,7)\). Está claro que \(g(x)\) es la gráfica que está más arriba ya que su punto de inflexión está en \(y= 7\) en comparación con \(f(x)\) cuyo punto de inflexión está en \(y = 4\). Como \(g(x)\) es ascendente y está 3 unidades por encima de \(f(x)\), que es descendente, puedes ver que las gráficas no se cruzan.
 Figura. 5 - Gráficas de \(f(x) = -(x- 6)^2 + 4\) y \(g(x) = (x-5)^2 + 7\)
Figura. 5 - Gráficas de \(f(x) = -(x- 6)^2 + 4\) y \(g(x) = (x-5)^2 + 7\)
Paso 2: Establece la integral.
\[\begin{align}\text{Área} & = \int_4^7 \left( y_{\text{top}} - y_{text{bottom}} \right) \, \mathrm{d}x \& = \int_4^7 \left[ (x-5)^2 + 7 -(-(x-6)^2 + 4) \right] \, \mathrm{d}x \& = \int_4^7 \left[ x^2 - 10x +25 + 7 - (-(x^2 -12x + 36) +4) \right] \, \mathrm{d}x \\& = \int_4^7 \left[ 2x^2 - 22x + 64 \right] \, \mathrm{d}x \\end{align}\]
Paso 3: Evalúa la integral.
\[\begin{align}\text{Área} & = \int_4^7 \left[ 2x^2 -22x + 64 \right] \, \mathrm{d}x \& = \left. \left(\frac{2}{3}x^3 - 11x^2 + 64x \right) \right|_4^7 \\& = 15\end{align}\].
Otra pregunta podría pedirte que calculases el área entre dos curvas sobre un intervalo en el que ambas curvas se encuentran por encima y por debajo en algún punto. El siguiente ejemplo muestra cómo podrías resolver una pregunta de este tipo:
Calcula el área de la región limitada por las gráficas de \(f(x) = -x^2 - 2x + 3\) y \(g(x) = x-1\) sobre el intervalo \([-4, 2]\).
Solución:
Paso 1: Determina qué gráfica está por encima dibujándolas como se muestra en la siguiente Fig. 6.
 Figura. 6 - Gráfica de una parábola y una recta
Figura. 6 - Gráfica de una parábola y una recta
Del esquema se deduce claramente que ambas gráficas están por encima en algún punto del intervalo dado.
Paso 2: Establece las integrales. En casos como éste, en el que cada gráfica se encuentra tanto por encima como por debajo, debes dividir el área que estás calculando en regiones separadas. El área total entre las dos curvas será entonces igual a la suma de las áreas de las regiones separadas.
En el esquema puedes ver que \(f(x)\) está por encima de \(g(x)\) en el intervalo \([-4, 1]\), por lo que ésa será la primera región, \(R_1\). También puedes ver que \(g(x) \) está por encima de \(f(x)\) en el intervalo \([1, 2]\), por lo que será la segunda región, \(R_2\).
\[\begin{align}\text{Área}_{R_1} & = \int_{-4}^1 \left( f(x) - g(x) \right) \, \mathrm{d}x \& = \int_{-4}^1 \left( -(x+1)^2 + 4 - (x-1) \right) \, \mathrm{d}x \& = \int_{-4}^1 \left( -x^2 - 2x + 3 - x + 1 \right) \, \mathrm{d}x \& = \int_{-4}^1 \left( -x^2 - 3x + 4 \right) \, \mathrm{d}x\end{align}\]
y
\\begin{align}\text{Area}_{R_2} & = \int_{1}^2 \left( g(x) - f(x) \right) \, \mathrm{d}x \& = \int_{1}^2 \left( x- 1 - (-(x+1)^2 + 4 ))\(- x^2 - 2x + 3) (derecha) () (=int_1}^2 (izquierda) (x^2 + 3x - 4 (derecha)) () (fin).
Paso 3: Evalúa las integrales.
\[\begin{align}\text{Area}_{R_1} & = \int_{-4}^1 \left( -x^2 - 3x + 4 \right) \, \mathrm{d}x \& = \left. \left( -\frac{1}{3}x^3 -\frac{3}{2}x^2 + 4x \right) \right|_{-4}^{1} \\& = \frac{125}{6}\end{align}\]
y
\[\begin{align}\text{Area}_{R_2} & = \int_{1}^2 \left( x^2 + 3x - 4 \right) \, \mathrm{d}x \& = \left. \left( \frac{1}{3}x^3 + \frac{3}{2}x^2 - 4x \right) \right|_1^2 \& = \frac{17}{6}\end{align}\]
Paso 4: Calcula el área total.
\[\begin{align}\text{Área total} & = \text{Área}_{R_1} + \text{Área}{R_2} \& = \frac{125}{6} + \frac{17}{6} \\& = \frac{71}{3}\end{align}\]
Otro ejemplo es el siguiente:
Calcula el área encerrada por las gráficas de \(f(x)\) y \(f(x)\) si \(h(x) = 3x^2 - 8x + 7\) y \(p(x) = x+ 1\).
Solución:
Paso 1: Determina la gráfica superior y el intervalo. Como se te pide que calcules el área de la región encerrada por \(f(x)\) y \(g(x)\), necesitas determinar las interceptas de las gráficas. La forma más sencilla de hacerlo es dibujar las gráficas como se muestra en la Fig. 7.
 Figura. 7 - Áreas entre una recta y una parábola
Figura. 7 - Áreas entre una recta y una parábola
En el esquema puedes ver que las dos gráficas encierran un área cuando \(g(x)\) está por encima de \(f(x)\). El intervalo en el que esto ocurre está comprendido entre las intersecciones de \(f(x)\) y \(g(x)\). Por tanto, el intervalo es \([1,2]\).
Paso 2: Establece la integral. Como \(g(x)\) está por encima de \(f(x)\), restarás \(f(x)\) de \(g(x)\).
\[\begin{align}\text{Área} & = \int_1^2 ( g(x) - f(x)) \, \mathrm{d}x \& = \int_1^2 ( x+1 - ( 3x^2 - 8x + 7)) \, \mathrm{d}x \& = \int_1^2 (-3x^2 + 9x - 6) \, \mathrm{d}x \\end{align}\]
Paso 3: Evalúa la integral.
\[\begin{align}\text{Área} & = \int_1^2 ( -3x^2 + 9x -6) \, \mathrm{d}x \& = \left. \left( -x^3 + \frac{9}{2}x^2 - 6x \right) \right|_1^2 \\& = 0,5\end{align}\]
Algunas preguntas pueden pedirte incluso que calcules el área delimitada por tres funciones, como en el ejemplo siguiente.
Se te dan las tres funciones siguientes:
\[\begin{gather*}f(x) = \frac{4}{x^2} \\\g(x) = 4x \\h(x) = \frac{1}{2} x\end{gather*}\]
Halla el área de la región delimitada por estas gráficas.
Solución:
El método para resolver esta pregunta es similar al utilizado en el ejemplo, en el que ambas gráficas están por encima y por debajo del intervalo. Es decir, esta pregunta se resuelve dividiendo el área total en regiones separadas.
Paso 1: En primer lugar, dibuja las gráficas como se muestra en la Fig. 8.
 Fig. 8 - Gráfica de tres curvas: dos rectas y una hipérbola
Fig. 8 - Gráfica de tres curvas: dos rectas y una hipérbola
En el croquis puedes ver que el área delimitada por las gráficas se extiende por el intervalo \([0,2]\), pero el cálculo del área se ha complicado porque ahora hay tres gráficas implicadas.
El secreto está en dividir el área en regiones separadas. El esquema te muestra que \(h(x)\) está por debajo de \(f(x)\) y de \(g(x)\) en \([0,2]\). Ahora sabes que \(f(x)\) y \(g(x)\) son gráficas superiores y, mediante cálculo o mirando tu croquis, puedes demostrar que se intersecan en \((1, 4)\). El valor \(x\) del punto donde se cruzan las gráficas es el lugar donde divides el área total en sus regiones separadas, como se muestra en la Fig.- 9 siguiente.
 Figura. 9 - El área delimitada por las dos rectas y las hipérbolas
Figura. 9 - El área delimitada por las dos rectas y las hipérbolas
La región \(R_1\) se extiende por el intervalo \([0,1]\) y está claramente delimitada en su parte superior por la gráfica de \(f(x)\). La región \(R_2\) se extiende por el intervalo \([1,2]\) y está limitada en su parte superior por la gráfica de \(f(x)\).
Ahora puedes calcular el área de las regiones \(R_1\) y \(R_2\), ya que has demostrado claramente que cada región tiene una gráfica superior y otra inferior.
Paso 2: Establece las integrales.
\[\begin{align}\text{Area}_{R_1} & = \int_0^1 \left( g(x) - h(x) \right) \, \mathrm{d}\x\& = \int_0^1 \left( 4x - \frac{1}{2}x \right) \, \mathrm{d}x \& = \int_0^1 \left( \frac{7}{2}x \right) \, \mathrm{d}x\end{align}\]
Y
\\begin{align}\text{Area}_{R_2} & = \int_1^2 \left( f(x) - h(x) \right) \, \mathrm{d}x \& = \int_1^2 \left( \frac{4}{x^2} - \frac{1}{2}x \right) \, \mathrm{d}x\end{align}\]
Paso 3: Evalúa las integrales.
\[\begin{align}\text{Area}_{R_1} & = \int_0^1 \left( \frac{7}{2}x \right) \, \mathrm{d}x \& = \left. \left( \frac{7}{4} x^2 \right) \right|_0^1 \\& = \frac{7}{4} \\\end{align}\]
Y
\\begin{align}\text{Area}_{R_2} &= \int_1^2 \left( \frac{4}{x^2} - \frac{1}{2}x \right) \, \mathrm{d}x \& = \left. \left( -\frac{4}{x} - \frac{1}{4}x^2 \right) \right|_1^2 \& = \frac{5}{4}\end{align}\]
Paso 4: Calcula el área total.\[\begin{align}\text{Área total} &= \text{Área}_{R_1} + \text{Área}_{R_2} \& = \frac{7}{4} + \frac{5}{4} \\& = 3\end{align}\]
Se te puede pedir que calcules el área entre dos curvas trigonométricas. El siguiente ejemplo te muestra cómo resolver cuestiones de esta naturaleza.
Calcula el área encerrada por las gráficas de \(f(x) = 4sin(x) \) y \(g(x) = cos(x) + 1\) para \(\pi \leq x \leq 2\pi\).
Solución:
Paso 1: Primero, dibuja las gráficas. Se cruzan una vez en el intervalo dado, en el punto \((0,\pi\). En el esquema puedes ver que la gráfica de \(g(x)\) está por encima de la gráfica de \(f(x)\) en todo el intervalo.
 Figura. 10 - Área encerrada por \(f(x)=\sin x\) y \(g(x)=\cos x+1\)
Figura. 10 - Área encerrada por \(f(x)=\sin x\) y \(g(x)=\cos x+1\)
Paso 2: Establece la integral. Como \(g(x)\) está por encima de \(f(x)\), tendrás que restar \(f(x)\) de \(g(x)\).
\[\begin{align}\text{Área} & = \int_{\pi}^{2\pi} (g(x) - f(x)) \& = \int_{\pi}^{2\pi} \left( \cos{x} + 1 - 4\sin{x} \right) \, \mathrm{d}x\end{align}\]
Paso 3: Evalúa la integral.
\[\begin{align}\text{Área} & = \int_{\pi}^{2\pi} \left( \cos{x} + 1 - 4\sin{x} \right) \, \mathrm{d}x \& = \left. \left( \sin{x} + x + 4\cos{x} \right) \right|_{\pi}^{2\pi} \& = \pi + 8 \\\ & = 11.14\end{align}\]
Área entre dos curvas polares
El área de la región de una curva polar \(f(\theta)\) limitada por los rayos \(\theta = \alfa) y \(\theta = \beta) viene dada por:
\[\frac{1}{2} \int_{\theta}^{\beta} r^{2} \, \mathrm{d}\theta = \frac{1}{2} \f(\theta)^2, \mathrm{d}\theta]
Entonces se deduce que la fórmula para calcular el área entre dos curvas polares es:
Si \(f(\theta)\) es una función continua, entonces el área limitada por una curva de forma polar \(r = f(\theta)\) y los rayos \(\theta = \alfa) y \(\theta = \beta) (con \(\alfa < \beta)) es igual a
$$ \frac{1}{2} \izquierda (f_2(\theta)^2 - f_1(\theta)^2 derecha) \, \mathrm{d}\theta $$
Puedes encontrar una explicación más detallada del área bajo curvas polares en el artículo Área de regiones delimitadas por curvas polares.
Área entre dos curvas - Puntos clave
- El área entre dos curvas con respecto al eje \(x) viene dada por \(\text{Área} = \int_a^b \left( f(x) - g(x) \right) \, \mathrm{d}x \), donde:
- \(f(x) \geq g(x) \) sobre el intervalo \([a,b]\).
- El área entre dos curvas con respecto al eje \(y) viene dada por \(\text{Área} = \int_c^d \left( g(y) - h(y) \right) \, \mathrm{d}x \), donde:
- \(g(y) \geq h(y)\) sobre el intervalo \([c,d]\).
- Ten en cuenta el área con signo al calcular el área entre dos curvas con respecto al eje \(y\)-. El área con signo a la izquierda del eje \(y) es negativa, y el área con signo a la derecha del eje \(y) es positiva.
- Si no se da ningún intervalo, se puede determinar calculando los interceptos de las gráficas dadas.

















