Funciones Logarítmicas: Definición, Propiedades

Saltar a un capítulo clave

Relación entre las funciones logarítmicas y las funciones exponenciales

La función logarítmica se define como la inversa de la función exponencial. Consulta Funciones inversas para obtener más detalles sobre cómo se relacionan exactamente las funciones y sus inversas, pero en resumen dos funciones f y g son inversas entre sí si

$f (g (x)) = x = g (f (x)) .$

Para más información sobre cómo se relacionan las funciones y sus inversas, consulta Funciones inversas .

Cuando observas las gráficas de una función exponencial y de la función logarítmica correspondiente, son reflexiones una de otra a través de la recta $y = x$ . En otras palabras, si el punto $(a, b)$ está en una de las gráficas, el punto $(b, a)$ está en la otra gráfica.

Gráfico de la función logarítmica natural que muestra que la exponencial y los logaritmos son inversos StudySmarter Funciones inversas | StudySmarter Originals

Reglas de las funciones logarítmicas

Utilizarás las reglas de los logaritmos:

$\log_{b} (1) = 0$
$\log_{b} (b) = 1$
Regla del producto: $\log_{b} (x) + \log_{b} (y) = \log_{b} (x y)$
Regla del cociente: $\log_{b} (\frac{x}{y}) = \log_{b} (x) - \log_{b} (y)$
Regla recíproca: $\log_{b} (\frac{1}{x}) = - \log_{b} (x)$
Regla de potencia: $\log_{b} (x^{n}) = n \cdot \log_{b} (x)$
Regla proporcional (fórmula de cambio de base): $\log_{b} (x) = \frac{\log_{a} (x)}{\log_{a} (b)}$

Simplifica la expresión $10^{\log_{100} (x)}$ .

Contesta:

Paso 1: Si fuera un logaritmo de base 10, la respuesta sería $x$ utilizando las propiedades de las funciones inversas. Así que la idea es utilizar la Regla de Proporción (también conocida como fórmula de cambio de base) paraconvertirlo primero en un logaritmo de base 10. Hay dos formas de hacerlo, y obtendrás la misma respuesta de ambas maneras.

La primera consiste en utilizar el hecho de que 10 es el número que elevas a una potencia:

$\log_{10} (x) = \frac{\log_{100} (x)}{\log_{100} (10)} = \frac{\log_{100} (x)}{\log_{100} (100^{\frac{1}{2}})} = \frac{\log_{100} (x)}{\frac{1}{2} \log_{100} (100)} = 2 \cdot \log_{100} (x)$

La segunda forma es mirar el logaritmo y ver que es de base 100, y utilizarlo para obtener

l o g_{100} (x) = \frac{l o g_{10} (x)}{l o g_{10} (100)} l o g_{100} (x) = \frac{l o g_{10} (x)}{2}

y luego resolver para $\log_{10} (x)$ para obtener $\log_{10} (x) = 2 \cdot \log_{100} (x) .$ Ambos métodos funcionan, y puedes utilizar el que te resulte más fácil de entender y recordar.

Así que tienes

$\log_{100} (x) = \frac{1}{2} \log_{10} (x)$

Paso 2: Utiliza ahora las propiedades de los exponentes,

$10^{\log_{100} (x)} = 10^{\frac{1}{2} \log_{10} (x)} = {(10^{\log_{10} (x)})}^{\frac{1}{2}} = x^{\frac{1}{2}}$

Así que la expresión $10^{\log_{100} (x)}$ completamente simplificada es

\sqrt{x} = x^{1 / 2}

Error común - Funciones logarítmicas

Siempre que utilices las reglas de los logaritmos, debes asegurarte de que utilizas valores para x que tengan sentido para la función, así como para la función exponencial, ya que son inversas.

Por ejemplo, no puedes intentar utilizar valores negativos para $x$ en $y = \log (x)$ porque la función exponencial $g (x) = b^{x}$ es siempre positiva. Un valor negativo de x haría $g (x)$ negativo (x e y cambian con inversos).Tampoco puedes utilizar una constante negativa para la base $b$ en un logaritmo porque no puedes utilizarla como base de una función exponencial.

Una función logarítmica es cualquier función de la forma $f (x) = \log_{b} (x)$ donde $x > 0$ , $b > 0$ y $b \neq 1$ . Esto se lee f(x) es igual a la base logarítmica b de x.

Cuando no se indica la base b, se considera que es 10. Así que $\log (x)$ significa lo mismo que $\log_{10} (x)$ .

¿Cuál es la inversa de la función $f (x) = \log (x)$ ?

Responde:

Recuerda que cuando no se indica ninguna base, se considera que es 10. Por tanto, la inversa de $f (x)$ es $f^{- 1} (x) = 10^{x}$ .

¿Cuál es la inversa de la función $g (x) = {(\frac{1}{2})}^{x}$ ?

Responde:

Recuerda que los inversos funcionan en ambos sentidos. Así que la inversa de $g (x)$ es $g^{- 1} (x) = \log_{\frac{1}{2}} (x)$ .

Enumera al menos 3 puntos de la gráfica de $f (x) = \log_{3} (x)$ sin representar gráficamente la función ni utilizar la calculadora.

Contesta:

Este problema parece más complicado de lo que realmente es. Ya sabes que la inversa de $f (x)$ es $f^{- 1} (x) = 3^{x}$ y que si $(a, b)$ es un punto de la gráfica de $f (x)$ entonces $(b, a)$ es un punto de la gráfica de $f^{- 1} (x)$ .

Paso 1: Las funciones exponenciales tienen una intersección y en $(0, 1)$ por lo que el punto $(1, 0)$ está en la gráfica de $f (x)$ .

Paso 2: Para obtener dos puntos más en la gráfica, evalúa los puntos de la gráfica de $f^{- 1} (x)$ . Elige dos valores aleatorios, $f^{- 1} (2) = 3^{2} = 9$ .

Paso 3: Evalúa otro punto de la gráfica de $f^{- 1} (x) = 3^{x} .$ $f^{- 1} (3) = 3^{3} = 27 .$

Paso 4: Entonces los puntos $(2, 9)$ y $(3, 27)$ están en la gráfica de $f^{- 1} (x)$ . Entonces sabes que los puntos $(9, 2)$ y $(27, 3)$ son puntos de la gráfica de $f (x)$ .

Así que, sin usar la calculadora, puedes ver que tres puntos de la gráfica de $f (x)$ son $(1, 0)$ , $(9, 2)$ y $(27, 3)$ .

Propiedades de la función logarítmica

Como ambas son equivalentes, puedes utilizar las propiedades de la función exponencial (ver Funciones exponenciales ) cuando pienses en las propiedades de las funciones logarítmicas. Una función exponencial no puede tener un número negativo por base, por lo que la base de la función logarítmica tampoco puede ser negativa. La función exponencial sólo toma valores positivos para y, por lo que la función logarítmica sólo puede utilizar números positivos para x.

Esto conduce a las siguientes propiedades de las funciones logarítmicas:

el dominio es $(0, \infty)$
el rango es $(- \infty, \infty)$
no hay intersección y
la intersección x está en $(1, 0)$
la asíntota vertical tiene la ecuación $x = 0$

Gráfica de funciones logarítmicas

Primero veamos algunos ejemplos graficados para ver cómo afecta la base b a la gráfica.

Aquí

$f (x) = \log_{2} (x) g (x) = \log_{4} (x) h (x) = \log_{8} (x) k (x) = \log_{16} (x)$

Funciones logarítmicas graficando diferentes bases StudySmarter Gráficas de logaritmos de distintas bases | StudySmarter Originals

Todas ellas

tienen la misma asíntota vertical en $x = 0$ .
tienen la misma intersección x en $(1, 0)$ .
son cóncavas hacia abajo
son funciones crecientes.

Veamos la base de las funciones del ejemplo y utilicemos la fórmula de cambio de base.

$g (x) = \log_{4} (x) = \frac{\log_{2} (x)}{\log_{2} (4)} = \frac{\log_{2} (x)}{\log_{2} (2^{2})} = \frac{\log_{2} (x)}{2 \cdot \log_{2} (2)} = \frac{1}{2 \cdot \log_{2} (2)} f (x) h (x) = \log_{8} (x) = \frac{\log_{2} (x)}{\log_{2} (8)} = \frac{\log_{2} (x)}{\log_{2} (2^{3})} = \frac{\log_{2} (x)}{3 \cdot \log_{2} (2)} = \frac{1}{3 \cdot \log_{2} (2)} f (x) k (x) = \log_{16} (x) = \frac{\log_{2} (x)}{\log_{2} (16)} = \frac{\log_{2} (x)}{\log_{2} (2^{4})} = \frac{\log_{2} (x)}{4 \cdot \log_{2} (2)} = \frac{1}{4 \cdot \log_{2} (2)} f (x)$

Así que en realidad son todos múltiplos constantes de $f (x)$ .

¿Y si, en lugar de eso, la base fuera una potencia fraccionaria de 2? Por ejemplo, si $f (x) = \log_{2} (x)$ pero ahora tienes

$m (x) = \log_{\frac{1}{2}} (x)$ , $n (x) = \log_{\frac{1}{4}} (x)$ y $p (x) = \log_{\frac{1}{8}} (x)$ entonces

m (x) = \log_{\frac{1}{2}} (x) = \log_{2^{- 1}} (x) = \frac{\log_{2} (x)}{\log_{2} (2^{- 1})} = - \frac{\log_{2} (x)}{\log_{2} (2)} = - \frac{1}{\log_{2} (2)} f (x) n (x) = \log_{\frac{1}{4}} (x) = \log_{2^{- 2}} (x) = \frac{\log_{2} (x)}{\log_{2} (2^{- 2})} = - \frac{\log_{2} (x)}{2 \cdot \log_{2} (2)} = - \frac{1}{2 \cdot \log_{2} (2)} f (x) p (x) = \log_{\frac{1}{8}} (x) = \log_{2^{- 3}} (x) = \frac{\log_{2} (x)}{\log_{2} (2^{- 3})} = - \frac{\log_{2} (x)}{3 \cdot \log_{2} (2)} = - \frac{1}{3 \cdot \log_{2} (2)} f (x)

lo que significa que de nuevo son múltiplos constantes de $f (x)$ pero también deben invertirse sobre el eje x.

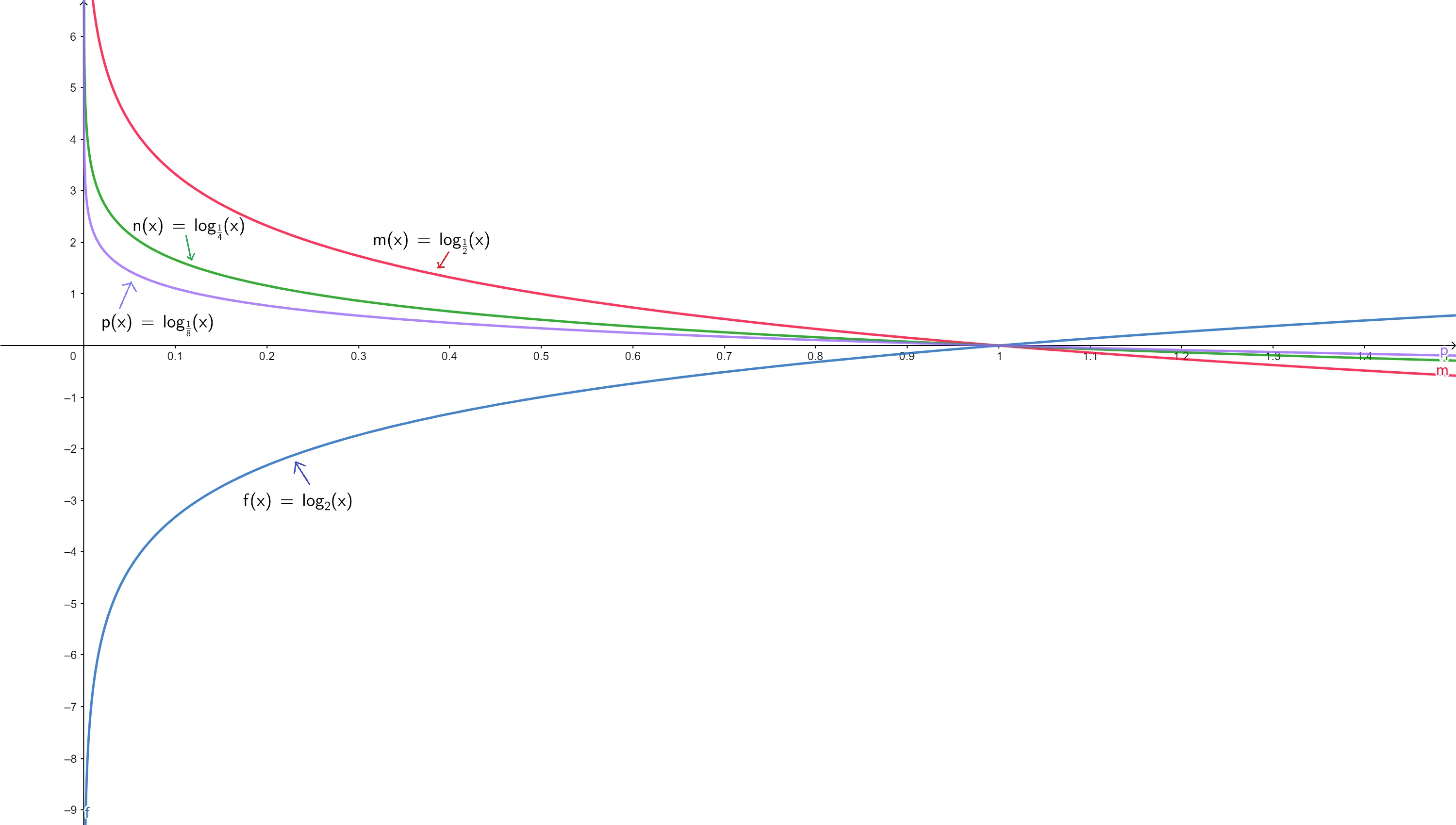
Gráfica de funciones logarítmicas comparando diferentes bases y concavidad StudySmarter

logaritmos con fracciones como base | StudySmarter Originals

Así que, como puedes ver, estas tres nuevas funciones son

decrecientes,
cóncavas hacia arriba,
tienen $x = 0$ como asíntota vertical, y
todas tienen la misma intersección x en $(1, 0)$ .

Ejemplos de funciones logarítmicas

Las funciones logarítmicas se utilizan para modelizar cosas como el ruido y la intensidad de los terremotos. Veamos algunos ejemplos reales en acción.

Los sonidos se miden en una escala logarítmica utilizando la unidad decibelios (dB). El sonido puede modelarse mediante la ecuación

d (p) = 10 \log (\frac{p}{p_{0}}) .

Donde

$p$ es la potencia del sonido
$p_{0}$ es el sonido más pequeño que puede oír una persona, y
$d (p)$ es el número de decibelios de la potencia $p$ :

Supongamos que estás pensando en comprar un nuevo altavoz. El altavoz A dice que tiene un nivel de ruido de 50 decibelios, mientras que el altavoz B dice que tiene un nivel de ruido de 75 decibelios. ¿Cuánto más intenso es el sonido del altavoz B que el del altavoz A?

Contesta:

Paso 1: Para comparar, llama $d_{A} (p)$ el nivel de decibelios del altavoz A, y $d_{B} (p)$ el nivel de decibelios del altavoz B. Por la información dada, sabes que

el altavoz A tiene $50 = 10 \log (\frac{A}{p_{0}})$ donde $A$ es la potencia del altavoz A
el altavoz B tiene $75 = 10 \log (\frac{B}{p_{0}})$ donde $B$ es la potencia del altavoz B

Paso 2: Si tomas la ecuación del altavoz A y la escribes en términos de $p_{0}$ te permitirá sustituirla en la ecuación del altavoz B. Así pues

$50 = 10 \log (\frac{A}{p_{0}}) 5 = \log (\frac{A}{p_{0}}) 10^{5} = 10^{\log (\frac{A}{p_{0}})} 10^{5} = \frac{A}{p_{0}} p_{0} = \frac{A}{10^{5}} .$

Paso 3: Sustituyendo esto en la ecuación del altavoz B,

$75 = 10 \log (\frac{B}{p_{0}}) 7.5 = \log (\frac{B}{\frac{A}{10^{5}}}) 7.5 = \log (\frac{10^{5} B}{A}) 10^{7.5} = 10^{\log (\frac{10^{5} B}{A})} 10^{7.5} = \frac{10^{5} B}{A} B = \frac{10^{7.5} A}{10^{5}} B \approx 316 A$

Por tanto, ¡el sonido del altavoz B es unas 316 veces más intenso que el del altavoz A!

Los terremotos se miden en una escala logarítmica llamada escala de Richter. La magnitud de un terremoto es una medida de cuánta energía se libera. Aquí $A_{0}$ es la amplitud de la onda más pequeña que puede medir un sismógrafo (el aparato que mide cuánto se mueve la tierra). Entonces la fórmula para medir un terremoto en la escala de Richter es

R (A) = \log (\frac{A}{A_{0}})

donde $A$ mide la amplitud de la onda del terremoto. En general, un terremoto mide entre 2 y 10 en la escala de Richter. Los que puntúan menos de 5 en la escala se consideran relativamente menores, y todo lo que supere un 8 en la escala es probable que cause bastantes daños. De hecho, un terremoto de magnitud 5 es 10 veces más potente que uno de magnitud 4.

Supongamos que un terremoto en Indiana tuvo una magnitud de 8,1 en la escala de Richter, pero otro ocurrido el mismo día en California fue 1,26 veces más intenso. ¿Cuál fue la magnitud del terremoto de California?

Responde:

Paso 1: Utilizando la definición de la escala de Richter, y usando $A_{I n d}$ para la amplitud del terremoto de Indiana, el terremoto de Indiana tuvo

R (A_{I n d}) = 8.1 = \log (\frac{A_{I n d}}{A_{0}}),

Paso 2: Llevando cada lado a la base 10 y resolviendo por

A_{I n d}

$10^{8.1} = 10^{\log (\frac{A_{I n d}}{A_{0}})} 10^{8.1} = \frac{A_{I n d}}{A_{0}} A_{I n d} = 10^{8.1} A_{0} .$

Ahora puedes utilizar el hecho de que el terremoto de California fue 1,26 veces más intenso que el de Indiana, o dicho de otro modo, si $A_{C a l}$ es la amplitud del terremoto de California, entonces $A_{C a l} = 1.26 A_{I n d}$ . Entonces

$R (A_{C a l}) = \log (\frac{A_{C a l}}{A_{0}}) = \log (\frac{1.26 A_{I n d}}{A_{0}}) = \log (\frac{1.26 \cdot 10^{8.1} A_{0}}{A_{0}}) = \log (1.26 \cdot 10^{8.1}) \approx 8.2$

Eso significa que el terremoto de California midió aproximadamente 8,2 en la escala de Richter.

Derivadas de funciones logarítmicas

La derivada de la función logarítmica es

$\frac{d}{d x} (\log_{a} x) = \frac{1}{x \cdot \ln (a)}$

Para obtener información sobre las derivadas de las funciones logarítmicas, consulta Derivada de la función logarítmica.

Funciones logarítmicas - Aspectos clave

$y = \log_{b} (x)$ es equivalente a $x = b^{y}$
la fórmula de una función logarítmica es $f (x) = \log_{b} (x)$ donde $x > 0$ , $b > 0$ y $b \neq 1$ .
$\log_{10} (x)$ es lo mismo que $\log (x)$
los logaritmos se utilizan para medir cosas como los decibelios y la fuerza de los terremotos

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Funciones Logarítmicas

¿Qué es una función logarítmica?

Una función logarítmica es una función inversa de una función exponencial, de la forma f(x) = log_b(x), donde b es la base.

¿Cómo se grafica una función logarítmica?

Para graficar una función logarítmica, identifica la base y traza puntos clave como (1,0). La gráfica pasa por estos puntos y se aproxima al eje Y sin tocarlo.

¿Cuáles son las propiedades de las funciones logarítmicas?

Las propiedades de las funciones logarítmicas incluyen: log_b(xy) = log_b(x) + log_b(y) y log_b(x^c) = c*log_b(x).

¿Para qué se utilizan las funciones logarítmicas?

Las funciones logarítmicas se utilizan en diversas áreas como la ciencia, la ingeniería, y la economía para modelar fenómenos de crecimiento y decaimiento.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 11 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Funciones Logarítmicas

Equipo editorial StudySmarter

Relación entre las funciones logarítmicas y las funciones exponenciales

Reglas de las funciones logarítmicas

Error común - Funciones logarítmicas

Propiedades de la función logarítmica

Gráfica de funciones logarítmicas

Ejemplos de funciones logarítmicas

Derivadas de funciones logarítmicas

Funciones logarítmicas - Aspectos clave

Aprende más rápido con las 0 tarjetas sobre Funciones Logarítmicas

Preguntas frecuentes sobre Funciones Logarítmicas

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Empresa

Nuestros productos

Ponte en contacto

Funciones Logarítmicas

Equipo editorial StudySmarter

Relación entre las funciones logarítmicas y las funciones exponenciales

Reglas de las funciones logarítmicas

Error común - Funciones logarítmicas

Propiedades de la función logarítmica

Gráfica de funciones logarítmicas

Ejemplos de funciones logarítmicas

Derivadas de funciones logarítmicas

Funciones logarítmicas - Aspectos clave

Aprende más rápido con las 0 tarjetas sobre Funciones Logarítmicas

Preguntas frecuentes sobre Funciones Logarítmicas

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Crea una cuenta gratuita para guardar esta explicación.

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.