Resumenes 
Flashcards 
StudySmarter AI 
Apuntes 
Plan de estudios 
Sets de estudio 
Repeticion espaciada 
Exámenes 
Magazine 
Hacer carrera 
Formacion Profesional 
Mobile App 
Saltar a un capítulo clave
Regresión
La regresión es la relación numérica entre dos variables (ahora necesitamos una variable independiente y otra dependiente). Normalmente nos fijamos en una regresión lineal; si nuestras dos variables son X e Y, buscamos una relación de la forma Y = mX + c. Esto significa que tendrá el aspecto de una línea recta en un gráfico de dispersión. A menudo nos referimos a una recta de regresión como recta de mejor ajuste.
¡Correlación no significa causalidad!
Es importante recordar que el hecho de que exista correlación no significa necesariamente que haya causalidad. Por ejemplo, podríamos encontrar una correlación entre el número de bomberos enviados a un incendio y la cantidad de daños creados por ese incendio. Como podemos deducir, el número de bomberos enviados no hace que se produzcan más daños, por lo que tenemos un caso con una correlación aparente pero sin causalidad. Esto significa que cuando examinamos supuestas correlaciones, debemos juzgar si esta correlación tiene causalidad.
Clasificación de la correlación
Cuando describimos la correlación, utilizamos dos medidas: la fuerza y la paridad.
Fuerza
Podemos describir la fuerza de una correlación entre dos variables.
Si hay una correlación fuerte, tenemos una relación fuerte entre las dos variables (es decir, hay un indicio fuerte de que existe una dependencia entre las variables). Si trazáramos una línea de regresión (línea de mejor ajuste), todos los puntos de datos estarían muy cerca de la línea.
Si hay una correlación débil, hay una relación más débil entre las dos variables (esto significa que hay menos indicios de que exista una dependencia entre las variables). Si hubiera una línea de regresión, los puntos estarían más separados de la línea.
Paridad
La paridad es una forma especial de decir si la correlación es positiva o negativa. Si hay una correlación positiva, significa que al aumentar una variable, aumenta la otra. En una recta de regresión, esto significa que el gradiente es positivo. Si la correlación es negativa, significa que a medida que una variable aumenta, la otra disminuye. En una recta de regresión, esto significa que el gradiente es negativo.
Si la correlación es lo suficientemente débil (hasta el punto de que no hay correlación real), entonces la llamamos correlación cero. Esto significaría que no podríamos trazar una recta de regresión.
A menudo utilizamos un coeficiente de correlación para describir la correlación, que varía de -1 a 1. La correlación positiva más fuerte se representa con 1, la correlación negativa más fuerte con -1, y una correlación nula con cero. Se trata de una escala móvil entre estos valores.
A continuación se muestran ejemplos de distintas correlaciones:
Correlación cero:
Gráfico de dispersión de correlación cero, Tom Maloy, StudySmarter Originals
Un ejemplo de algo sin correlación sería la talla de calzado de los niños en el Reino Unido y el número de girasoles en Francia. No están relacionados y, por tanto, ninguno influye en el otro, por lo que no hay correlación.
Una correlación positiva fuerte:
Gráfico de dispersión de correlación positiva fuerte, Tom Maloy, StudySmarter Originals
Un ejemplo de correlación positiva fuerte serían las horas pasadas bajo la luz solar directa y la gravedad de las quemaduras solares. A medida que aumenta una de estas variables, también lo hace la otra.
Una correlación negativa fuerte:
Gráfico de dispersión de correlación negativa fuerte, Tom Maloy, Study Smart Originals
Un ejemplo de correlación negativa fuerte sería la velocidad de un tren frente al tiempo para completar un trayecto de una estación a la siguiente. A medida que aumenta la velocidad, disminuye el tiempo hasta el destino. Como se trata de una relación física, estará fuertemente relacionada.
Una correlación positiva débil:
Gráfico de dispersión de correlación positiva débil, Tom Maloy, StudySmarter Originals
Un ejemplo de correlación positiva débil puede ser la prescripción de un fármaco concreto y el aumento de la insuficiencia renal. Es poco probable que el fármaco provoque insuficiencia renal a todo el mundo, pero aumentará la probabilidad en algunas personas.
Una correlación negativa débil:
Gráfico de dispersión de correlación negativa débil, Tom Maloy, StudySmarter Originals
Un ejemplo de correlación negativa débil serían las lecciones perdidas y las calificaciones finales. En general, el número de lecciones perdidas disminuiría las calificaciones; sin embargo, esto diferirá de un estudiante a otro para acabar con una relación más débil.
Un ejemplo real de correlación y regresión
Hay muchos ejemplos de correlación y regresión en la vida real. En la pandemia de COVID-19, muchos gobiernos habrán hecho un seguimiento de las muertes/hospitalizaciones/números de casos de COVID en relación con diversas métricas, como la edad, el peso o la ubicación, para intentar encontrar un patrón y ver dónde se necesitaría más ayuda. Primero se estudiaría la correlación para ver si hay algún patrón aparente, y luego se utilizaría la regresión para intentar predecir los valores de los datos que falten.
Ejemplo de pregunta sobre correlación y regresión
P: A continuación se muestra una tabla con los datos de los alumnos de una clase, en la que se midió la altura y la longitud de los brazos.
Altura (cm) | 127 | 135 | 142 | 151 | 158 | 161 | 163 | 170 | 176 |
Longitud del brazo (cm) | 70 | 75 | 82 | 89 | 91 | 95 | 88 | 98 | 103 |
Dibuja un gráfico de dispersión para representar los datos
Describe la correlación entre los conjuntos de datos
Utiliza una recta de regresión para predecir la longitud del brazo de una persona que mide 165 cm.
A:
Representemos esto con la altura en el eje x y la longitud del brazo en el eje y. Esto se parece a
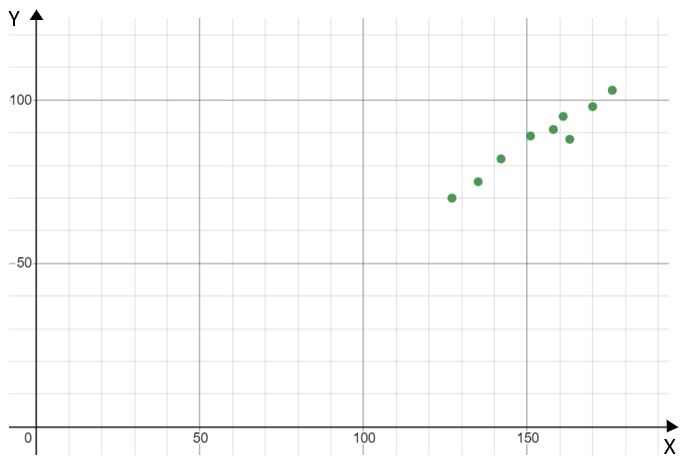
Observando el gráfico de dispersión, a medida que aumenta la altura, también lo hace la longitud del brazo, lo que significa que existe una correlación positiva. Si trazáramos una recta de regresión sobre el gráfico, los puntos se acercarían a esta recta, lo que significa que existe una fuerte correlación positiva entre la longitud del brazo y la altura.
Nuestro primer paso aquí es dibujar nuestra recta de regresión. Debería tener este aspecto:
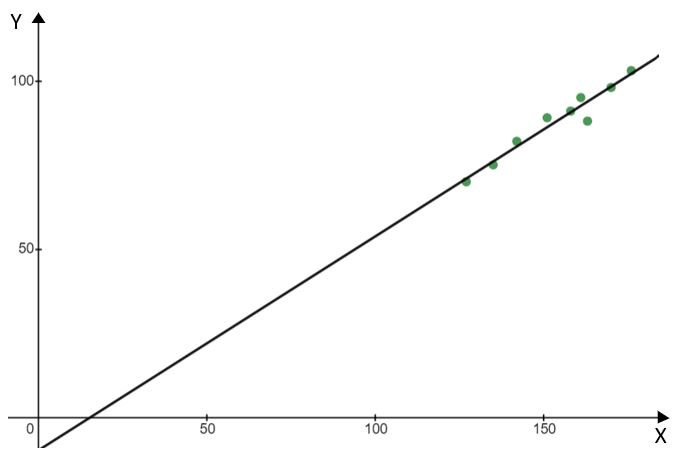
A partir de este punto, trazamos una recta de x = 165 y vemos dónde se cruza con la recta de regresión. Entonces, el valor y de este punto de intersección será nuestra estimación de la longitud del brazo.
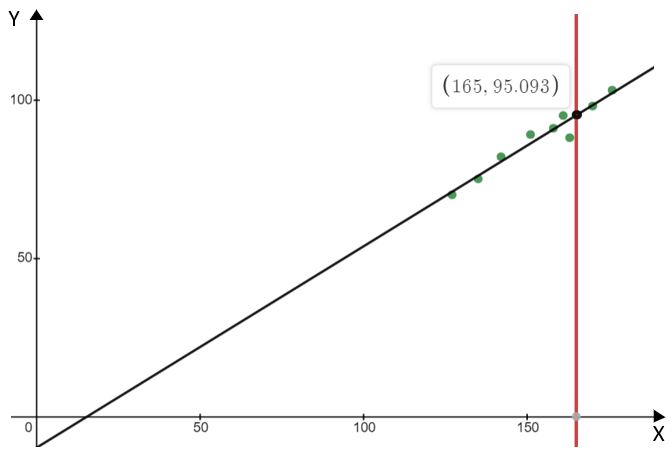
Esto significa que nuestra estimación de la longitud del brazo es de 95 cm.
Correlación: puntos clave
Una correlación fuerte significa que las variables parecen depender unas de otras.
Una correlación débil significa que hay menos pruebas que sugieran que existe una dependencia entre ellas.
Una correlación positiva parece tener un gradiente positivo.
Una correlación negativa parece tener un gradiente negativo.
Aprende más rápido con las 0 tarjetas sobre Correlación
Regístrate gratis para acceder a todas nuestras tarjetas.
Preguntas frecuentes sobre Correlación
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más