En un entorno de Probabilidad, el conjunto de todo lo que consideramos en un diagrama de Venn se denomina espacio muestral, y denotamos el espacio muestral por 𝛏 (la letra griega xi en minúscula). Un ejemplo de conjunto serían los alumnos de un colegio o las personas que van al gimnasio. De forma más general, entendemos por conjunto un grupo de puntos de datos en Estadística.
A menudo sólo necesitamos considerar dos tipos de diagramas de Venn: los que tienen dos subconjuntos y los que tienen tres.
¿Cómo se dibuja un diagrama de Venn?
Para dibujar un diagrama de Venn, podemos seguir una serie de pasos lógicos. Primero veremos cómo dibujar un diagrama para dos subconjuntos del espacio muestral. De momento, los llamaremos A y B.
Paso1: Dibuja dos círculos, que tengan una sección superpuesta en el centro.
Paso2: Dibuja un rectángulo alrededor del exterior de estos dos círculos, dejando espacio entre los círculos y el rectángulo.
Paso3: Rotula el rectángulo con 𝛏, hazlo por fuera. Este rectángulo representa todo nuestro espacio muestral.
Paso4: Etiqueta un círculo A, y el otro B, ya que representan nuestros dos subconjuntos.
El resultado debería tener este aspecto:
Ejemplo de diagrama de Venn con dos subconjuntos del espacio muestral , Tom Maloy - StudySmarter Originals
Para tres subconjuntos del espacio muestral, digamos A, B y C, seguimos pasos similares pero con tres círculos superpuestos, como se ve a continuación.
Ejemplo de diagrama de Venn con tres subconjuntos del espacio muestral, Tom Maloy - StudySmarter Originals
Ejemplos de diagramas de Venn
Para entender cómo funcionan los diagramas de Venn, veamos los siguientes ejemplos de diagramas de Venn.
Supongamos que tenemos una clase de 40 alumnos, 22 juegan al fútbol, 16 al rugby y 8 juegan a ambas cosas. Dibujemos primero el diagrama de Venn sin rellenar ningún valor. Esto nos da
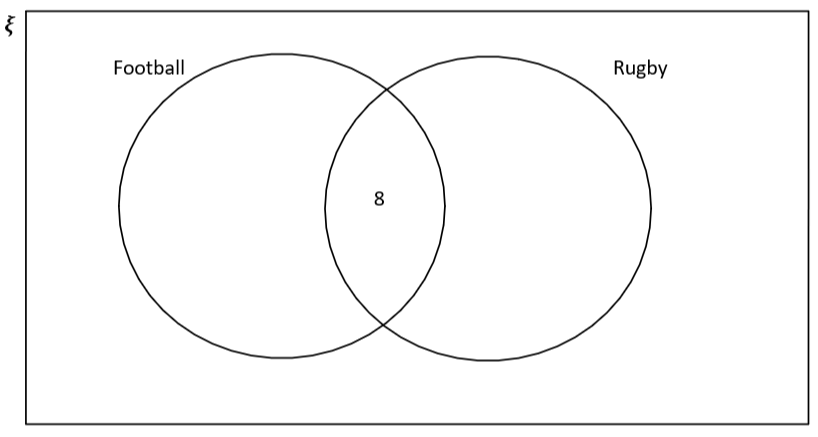
El primer dato que podemos rellenar es que podemos poner 8 en la sección de intersección de los círculos, ya que 8 alumnos juegan tanto al rugby como al fútbol. Esto nos da
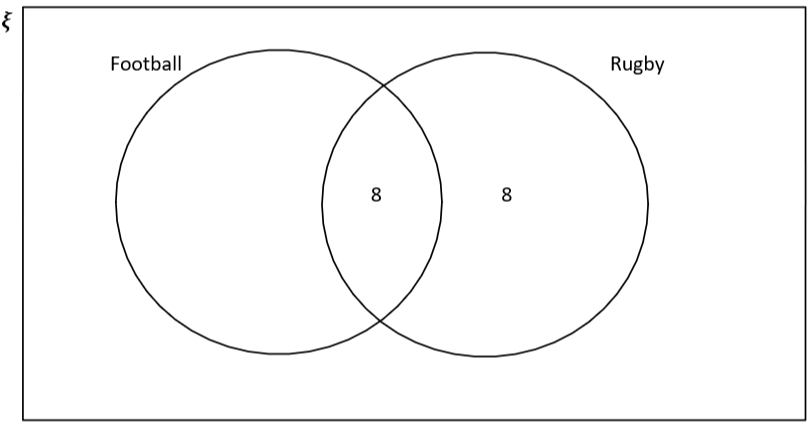
Un total de 16 personas juegan al rugby, lo que incluye a las 8 que juegan a ambas cosas. Eso significa que en la sección que es sólo de rugby, deberíamos poner 16-8=8.
Un total de 22 personas juegan al fútbol, y eso incluye a las 8 que juegan a ambas cosas, lo que significa que tenemos 22-8=14 en la sección que representa al fútbol.
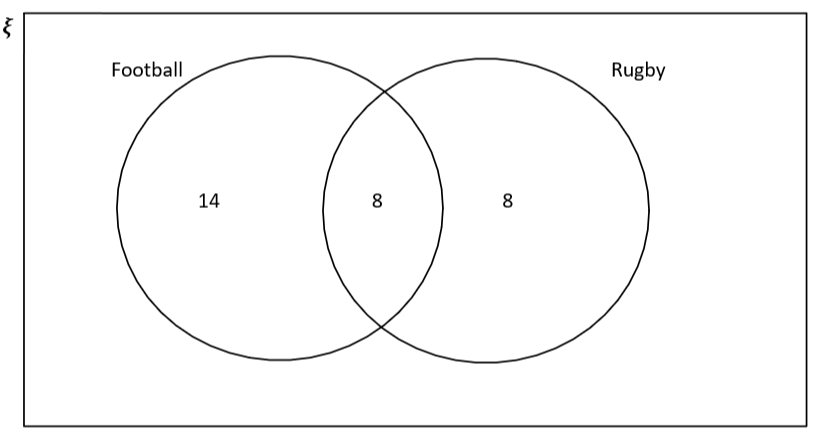
Tenemos 40 alumnos en clase. Este es nuestro espacio muestral, lo que significa que todos nuestros números deben sumar 40. 14+8+8=30, lo que significa que 10 personas no practican ninguno de los dos deportes y deben colocarse en el rectángulo, pero no en ninguno de los dos círculos.
Este es ahora nuestro diagrama de Venn completo para la situación que hemos descrito.
Entrevisté a algunos estudiantes universitarios. 25 hacen matemáticas, 20 física y 19 química. 1 estudiante hace las tres cosas, y 3 no hacen ninguna de las anteriores. 2 estudiantes hacen matemáticas, química y no física, 5 estudiantes hacen física y química sin matemáticas, y 8 estudiantes hacen matemáticas y física sin química. Dibuja un diagrama de Venn para mostrar estos datos.
Lo primero es lo primero: dibujemos el contorno del diagrama y rellenemos la información que se nos da. El resultado es
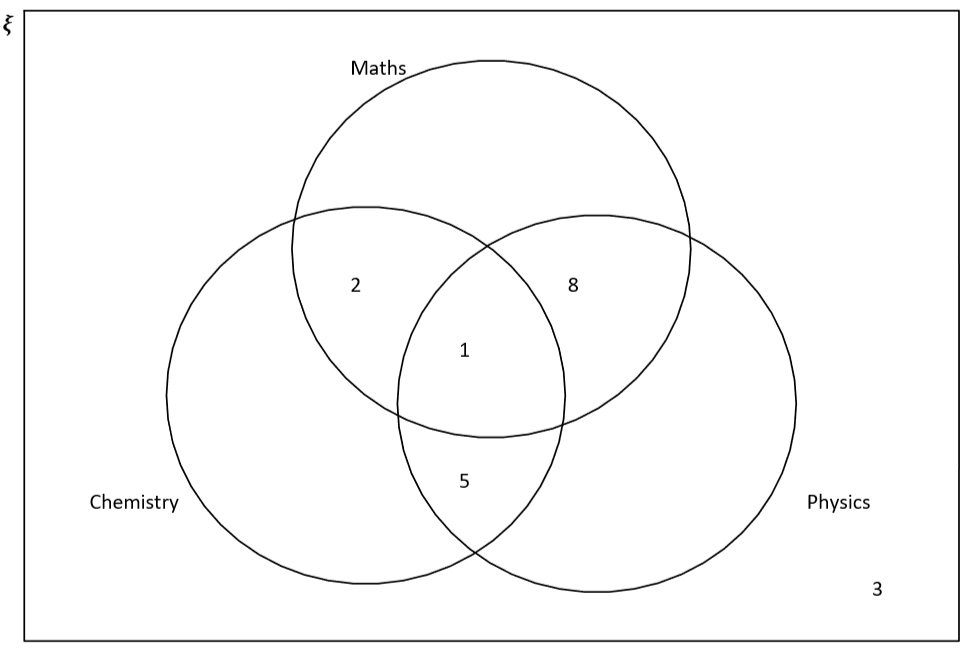
Ahora tenemos que sumar los números para encontrar los valores que faltan. 25 hacen matemáticas, por lo que el Número de personas que sólo hacen matemáticas viene dado por 25-2-1-8, que da 14. Hacemos lo mismo para física y química, por lo que el número de alumnos que hacen sólo física viene dado por 20 -8-1-5=6. Los alumnos que sólo hacen química vienen dados por 19-2-1-5=11. Esto significa que podemos completar el diagrama de Venn de la siguiente manera:
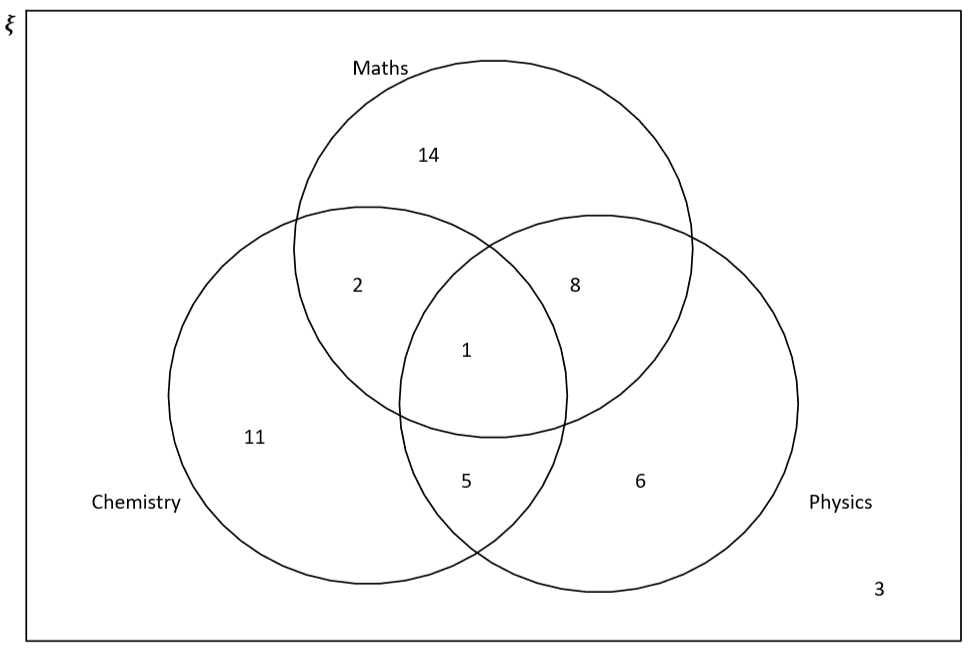
Operadores lógicos sobre conjuntos
Cuando tenemos varios conjuntos actuando conjuntamente, podemos describir partes de ellos utilizando operadores lógicos. Todos estos símbolos son comunes siempre que hablamos de la Notación del diagrama de Venn.
Unión de conjuntos
La unión de conjuntos, denotada por ∪, es un operador lógico que podemos utilizar sobre los conjuntos. Cuando veamos este operador, debemos pensar en sustituirlo por "o". Por ejemplo, si denoto A=personas a las que les gusta el rugby y B=personas a las que les gusta el críquet, y escribo la afirmación A∪B, lo interpretaríamos como "las personas a las que les gusta el críquet o las personas a las que les gusta el rugby o las personas a las que les gustan ambas cosas". En un diagrama de Venn, si sombreara A∪B, quedaría así:
Unión de 2 conjuntos, Tom Maloy, Study Smarter Originals
Por tanto, para que un objeto esté en A∪B, tiene que estar en cualquiera de los dos conjuntos.
Intersección de conjuntos
La intersección de conjuntos es un operador lógico diferente que utilizamos en los conjuntos y se denota por ∩. Cuando veamos este operador, debemos pensar en sustituirlo por "y". Con A y B denotados como arriba, si viéramos A∩B, deberíamos interpretarlo como "Personas a las que les gusta el críquet y el rugby". En un diagrama de Venn, quedaría así:
Intersección de 2 conjuntos, Tom Maloy, Study Smarter Original
Para que un objeto esté en A∩B, tiene que estar en ambos conjuntos.
Complemento de conjuntos
El último operador lógico que debemos conocer es el complemento, en el que debemos pensar como "no". Si quisiera escribir el complemento de A, podría escribir o bien A' o bien .
De nuevo con A como arriba, interpretaríamos como "el conjunto de personas a las que no les gusta el rugby". En un diagrama de Venn, esto se vería así:
Complemento de un conjunto, Tom Maloy, Study Smarter Originals
¿Cómo se representa la probabilidad mediante diagramas de Venn?
Como hemos dicho antes, los diagramas de Venn pueden ayudarnos a determinar probabilidades. Por ejemplo, si nos fijamos en el ejemplo 2 anterior, podríamos plantear una pregunta como "hallar la Probabilidad de que un alumno sólo estudie una de las asignaturas de matemáticas, física o química". En este caso, utilizaríamos la ecuación general de probabilidadque nos da .
Dos sucesos son mutuamente excluyentes si no pueden ocurrir al mismo tiempo. En un diagrama de Venn, esto significaría que la intersección está vacía, y si A y B son mutuamente excluyentes, P(AB)=0.
Sea el espacio muestral los Números Enteros del 1 al 10. Dibuja un diagrama de Venn con los Números Primos y los números pares como nuestros dos conjuntos. Halla la probabilidad de elegir un Número que sea par pero no primo.
Escribamos primero todos los números que son primos entre 1 y 10 y hagamos lo mismo para los números pares.
Primos: 2,3,5,7
Pares: 2,4,6,8,10
Esto significa que sólo tenemos 2 en la intersección, lo que da un diagrama de Venn de
Entonces P(elegir un número que sea par pero no primo)=número de números que son pares pero no primos números totales=
Relaciones lógicas en un diagrama de Venn
También se nos puede pedir que sombreemos un diagrama de Venn basándonos en una relación lógica, y tenemos un método para hacerlo, como se muestra a continuación.
Supongamos que tenemos una relación lógica entre dos conjuntos, digamos A y B. (por ejemplo, A'∪B o A∩B')
Paso 1: Sombrea de un color la relación lógica sobre A.
Paso 2: Sombrea de otro color la relación lógica sobre B.
Paso3: Si los dos sucesos (A y B) están relacionados por una unión, nuestro diagrama mostrará la relación donde haya algún sombreado. Si se trata de una intersección, estaría donde haya sombreado de ambos.
Sombrea la relación A'∩B
Paso 1: Sombrea A':
Paso 2: Sombrea B con otro color
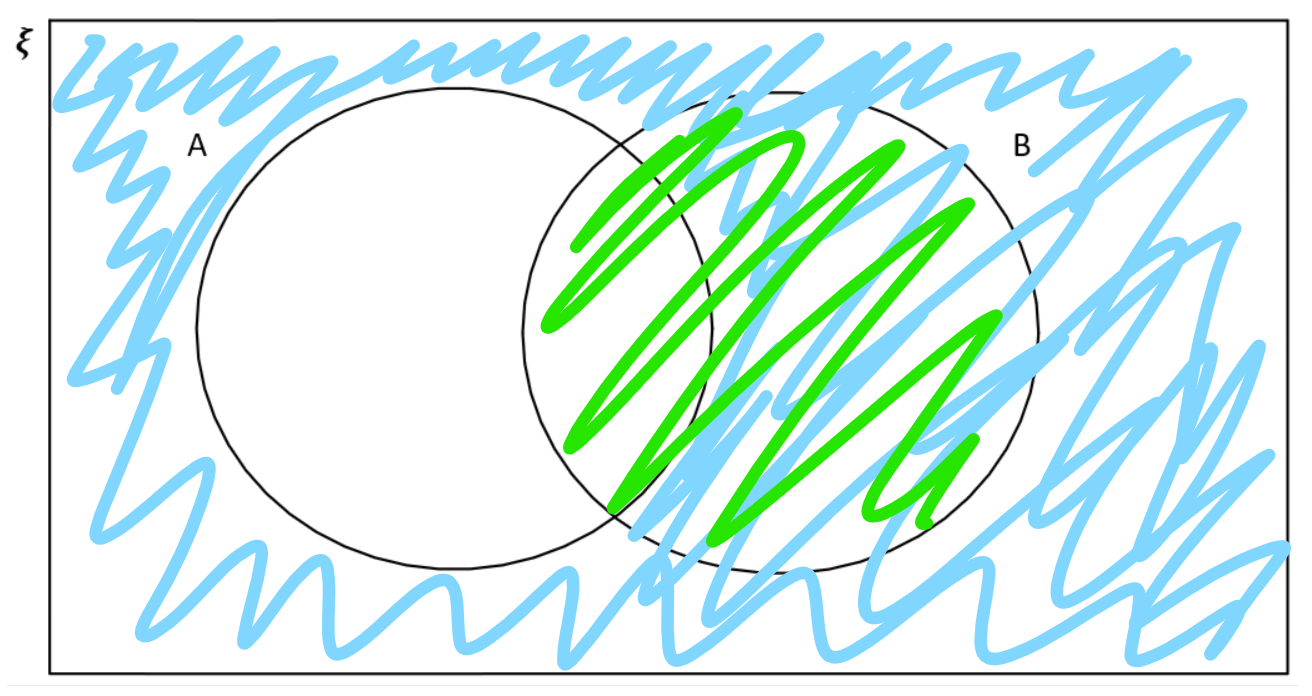
Paso 3: Como esto está en una intersección, ahora sabemos que A'∩B está representado por las regiones donde hay ambos colores, como se muestra a continuación.
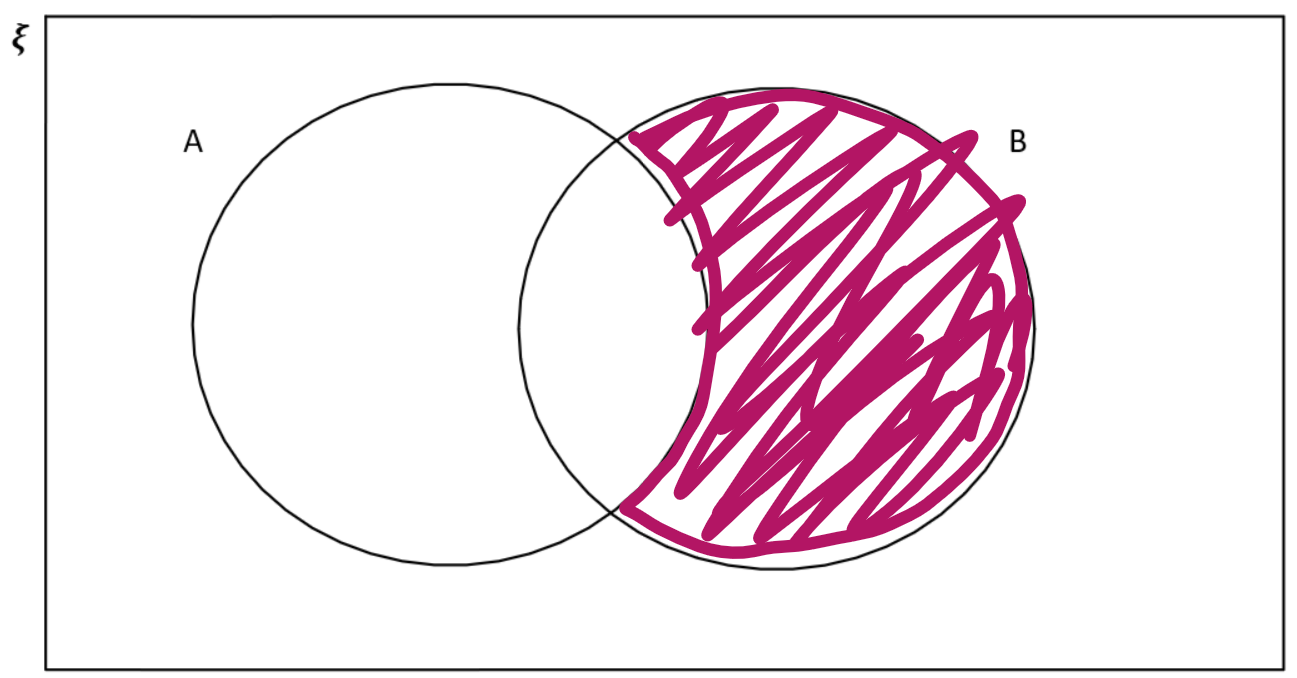
Sombrear la relación (AUB)
Paso 1: Sombrear AUB
Paso 2: (AUB)' sería el área que no está sombreada en lo anterior:
Diagramas de Venn - Puntos clave
El símbolo ⋃ representa la unión de conjuntos.
El símbolo ∩ representa la intersección de conjuntos.
El símbolo ξ representa el espacio muestral.
Todos nuestros puntos de datos deben aparecer dentro del espacio muestral.
Aprende con 0 tarjetas de Diagramas de Venn en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Diagramas de Venn
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
