Radianes: Ángulo, Grados y Fórmula

ÍNDICE DE TEMAS :

ÍNDICE DE TEMAS

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Los grados son la medida de ángulo más conocida que puede utilizarse en trigonometría. Una alternativa es el concepto de radianes.

En primer lugar veremos qué son los radianes.
A continuación, demostraremos cuántos radianes tiene una circunferencia.
Luego aprenderemos a resolver las ecuaciones trigonométricas utilizando radianes.
Te mostraremos una tabla de conversión de radianes a grados.

¿Qué son los radianes?

Los radianes son una unidad angular alternativa que tiene más sentido si consideramos una circunferencia; así que vamos a hacerlo.

Radianes en una circunferencia

Una circunferencia tiene \(360^\circ\) o \(2\pi\,\mathrm{rad}\).

Vamos a demostrar esto paso a paso, usando una circunferencia y un triángulo rectángulo.

Paso 1: empecemos por dibujar una circunferencia con un radio unitario (radio de \(1\)) en el que movemos el radio para formar un ángulo que llamaremos \(\theta\):

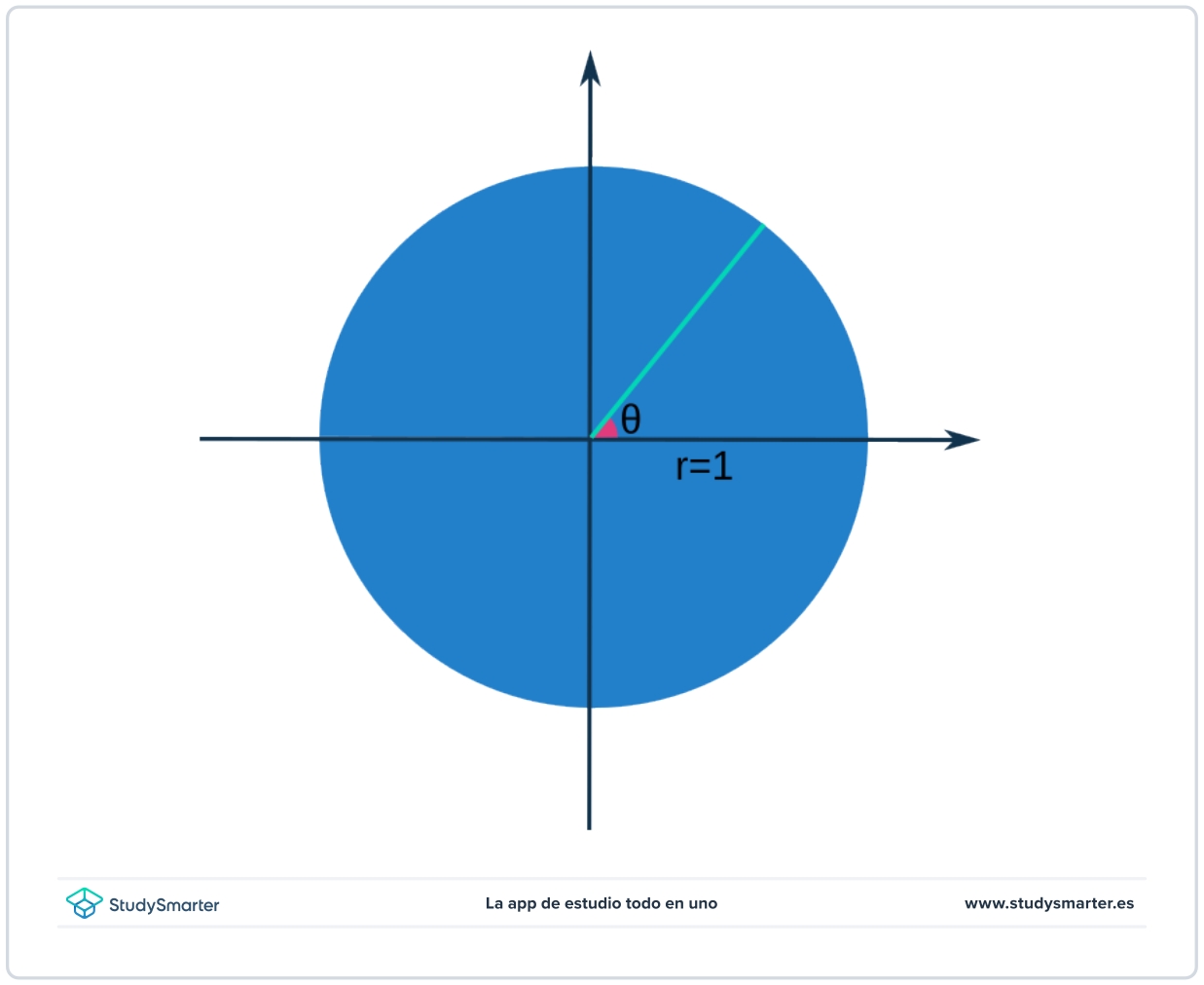
Radianes, Circunferencia unitaria, StudySmarter

Fig. 1: Circunferencia unitaria en la que se observa un sector formando un ángulo.

Paso 2: ahora vamos a dibujar un lado para que esto sea un triángulo rectángulo. Etiquetamos este lado como \(x\):

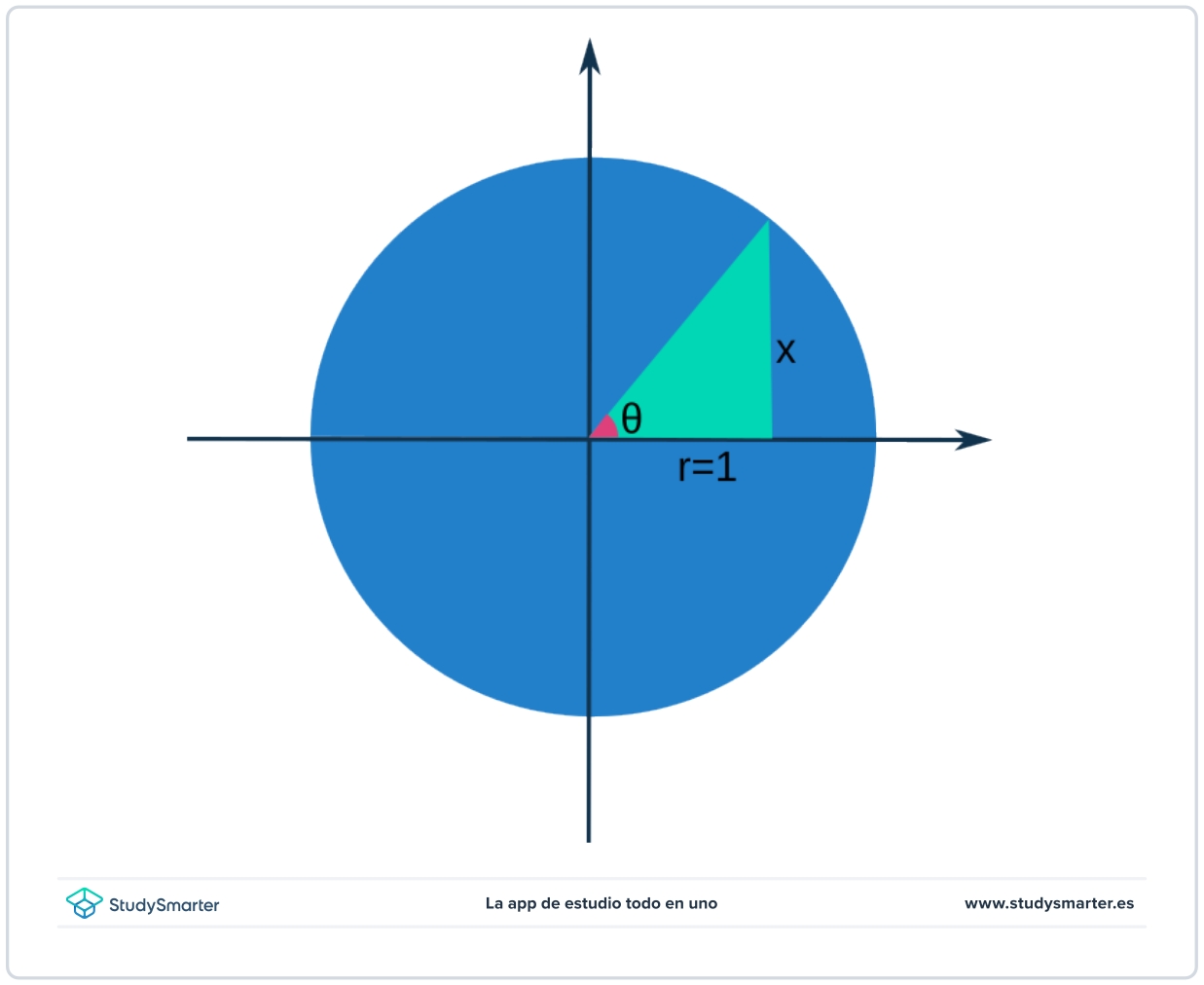
Radianes, Circunferencia unitaria, StudySmarter

Fig. 2: Circunferencia unitaria con un triángulo rectángulo formado con su radio.

Paso 3: ahora podemos usar la trigonometría para escribir un cálculo para \(x\) como: \(x=r \sin(\theta)\).

Paso 4: ahora podemos pensar qué pasaría si el radio recorriera todo el camino alrededor de la circunferencia. El radio recorrería una distancia de \(2 \pi\). Esto se debe a que la longitud de la circunferencia es de \(2 \pi\).

Por lo tanto: \(360^\circ=2 \pi \,\mathrm{rad}\).

Esa es nuestra conversión clave: \(\pi \text{ radianes}=180^\circ\).

¿Cómo resolvemos las ecuaciones trigonométricas utilizando radianes?

Para ello se utilizan exactamente los mismos métodos trigonométricos que cuando se utilizan los grados. Puedes ajustar una calculadora para que muestre las respuestas en radianes.

Encuentra el valor del ángulo \(CAB\) y da tu respuesta en radianes.

Radianes, triángulo rectángulo, StudySmarter Fig. 3: Triángulo rectángulo.

Solución:

Pregunta estándar de trigonometría: averiguar cuál de las relaciones trigonométricas estamos usando. Tenemos opuesto y adyacente, así que es la tangente:

\[\tan(CAB)=\dfrac{4}{7}\]

Por lo tanto, tenemos que realizar una función trigonométrica inversa, por lo que tenemos:

\[\tan\left( \dfrac{4}{7} \right) =0{,}519...\]

Recuerda asegurarte de que tu calculadora esté en radianes antes de realizar este último paso.

Entonces, el ángulo \(CAB\) es de:

\[0{,}519...\]

Veamos otro ejemplo como este:

Encuentra el valor de \(x\).

Radianes, Triángulo con medidas desconocidas, StudySmarter Fig. 4: Triángulo con un ángulo y dos lados desconocidos.

Solución:

Aquí podemos usar la regla del seno; por lo tanto:

\[\dfrac{8}{ \sin \left( \dfrac{5 \pi}{8} \right)}=\dfrac{x}{ \sin \left( \dfrac{\pi}{8} \right)}\]

\[ \sin \left( \dfrac{\pi}{8} \right) \cdot \left( \dfrac{8}{\sin \left( \dfrac{5 \pi}{8}\right)} \right)\]

Asegúrate de que tu calculadora está correctamente configurada en radianes. Esto significa que el resultado es:

\[x=3{,}31\,\mathrm{cm}\]

Hemos visto cómo se puede convertir la calculadora en forma de radianes. Ahora vamos a ver cómo podemos convertir directamente entre radianes y grados.

Conversión de radianes a grados

Hay una conversión clave:

Grados \(\rightarrow\) Radianes: \(x \cdot \dfrac{\pi}{180}\)

Y viceversa:

Radianes \(\rightarrow\) Grados: \(x \cdot \dfrac{180}{\pi}\)

Veamos esto en acción.

Convertir \(38^\circ\) a radianes.

Solución: \(\dfrac{38}{180} \cdot \pi = 0{,}663...\) radianes.

Y veamos un ejemplo en sentido inverso.

Pasar \(0{,}285\) radianes a grados.

Solución: \(\dfrac{0{,}285}{\pi} \cdot 180 = 16{,}329^\circ...\)

Conversiones importantes a radianes: 90 grados, 30 grados, etc.

En la siguiente tabla podemos ver algunas conversiones estándar entre grados y radianes:

Grados	Radianes
\(30^\circ\)	\(\dfrac{\pi}{6}\)
\(45^\circ\)	\(\dfrac{\pi}{4}\)
\(60^\circ\)	\(\dfrac{\pi}{3}\)
\(90^\circ\)	\(\dfrac{\pi}{2}\)
\(180^\circ\)	\(\pi\)
\(360^\circ\)	\(2\pi\)

Tabla 1: grados y radianes.

Radianes - Puntos clave

Los radianes son una unidad angular como los grados, pero con una pequeña conversión.
Recuerda que \(\pi\) radianes = \(180^\circ\).
Al resolver problemas de trigonometría o ecuaciones el método es exactamente el mismo con radianes y grados.
Recuerda poner la unidad angular en radianes en tu calculadora. Esto simplificará las respuestas a los problemas.
Para convertir radianes a grados, multiplica por: \(\dfrac{\pi}{180}\).
Para convertir grados a radianes, multiplica por: \(\dfrac{180}{\pi}\).

Preguntas frecuentes sobre Radianes

2π radianes.

Numéricamente es dos veces 3,14159. En grados son 360 grados.

Es una medida del ángulo plano, alternativa a los grados. Surge del concepto de un arco de circunferencia que tiene la misma longitud que el radio de la circunferencia. El ángulo que este arco abarca es un radián.

Multiplica el ángulo en grados por π/180, donde π es el número pi, cuyo valor aproximado es 3,14159.

Pon a prueba tus conocimientos con tarjetas de opción múltiple

TU PUNTUACIÓN

Tu puntuación:

¿Ya tienes una cuenta? Iniciar sesión

REGISTRARSE REGISTRARSE

Tarjetas en Radianes15 Empieza a aprender

Es una medida alternativa para medir un ángulo en grados:

Radianes.

Escribe la fórmula para coordenada \(x\) de un punto en la circunferencia del círculo unitario.

\(x=r\sin(θ)\).

\(360^o\) es igual a:

\(2\pi rad\).

\(180^o\) es igua al:

(\pi rad\).

¿Cómo convertir grados a radianes?:

Multiplicas por \(\pi\) y divides entre \(180^o\).

Convierte \(30^o\) a radianes.

\(0,5235\).

Aprende con 15 tarjetas de Radianes en la aplicación StudySmarter gratis

Regístrate con email REGISTRARSE REGISTRARSE

¿Ya tienes una cuenta? Iniciar sesión

Conoce más sobre Radianes

Resúmenes

Flashcards

Radianes

¿Qué son los radianes?

Radianes en una circunferencia

¿Cómo resolvemos las ecuaciones trigonométricas utilizando radianes?

Conversión de radianes a grados

Conversiones importantes a radianes: 90 grados, 30 grados, etc.

Radianes - Puntos clave

Preguntas frecuentes sobre Radianes

Pon a prueba tus conocimientos con tarjetas de opción múltiple

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Entdecke Lernmaterial in der StudySmarter-App

Radianes

¿Qué son los radianes?

Radianes en una circunferencia

¿Cómo resolvemos las ecuaciones trigonométricas utilizando radianes?

Conversión de radianes a grados

Conversiones importantes a radianes: 90 grados, 30 grados, etc.

Radianes - Puntos clave

Preguntas frecuentes sobre Radianes

¿Cuántos radianes son 360 grados?

¿Cuánto es 2 pi?

¿Cuál es la definición de un radián?

¿Cómo se calculan los radianes?

Pon a prueba tus conocimientos con tarjetas de opción múltiple

¡Únete a la aplicación StudySmarter y aprende de manera eficiente con millones de tarjetas y mucho más!

Aprende con 15 tarjetas de Radianes en la aplicación StudySmarter gratis

Aprende con 15 tarjetas de Radianes en la aplicación StudySmarter gratis

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.

This is still free to read, it's not a paywall.

You need to register to keep reading

This is still free to read, it's not a paywall.

You need to register to keep reading

Crea una cuenta gratuita para guardar esta explicación.

Entdecke Lernmaterial in der StudySmarter-App

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.