Rombos: 'Geometría', 'Propiedades'

Saltar a un capítulo clave

Significado de los rombos

Un rombo es un cuadrilátero con todos los lados de igual longitud y dos pares de lados paralelos.
Un cuadrilátero es cualquier forma decuatro lados.
Un paralelogramo es cualquier cuadrilátero con dos pares de lados paralelos.

Un cuadrilátero con 2 pares de lados opuestos paralelos se llama paralelogramo.

A partir de la definición de rombo y paralelogramo, vemos que todos los rombos son tipos especiales de paralelogramos, ya que tienen dos pares de lados paralelos. A efectos de este artículo, resulta útil estar familiarizado con los paralelogramos.

La siguiente figura ilustra un rombo, $A B C D$ . Como es un rombo, todos sus lados tienen la misma longitud.

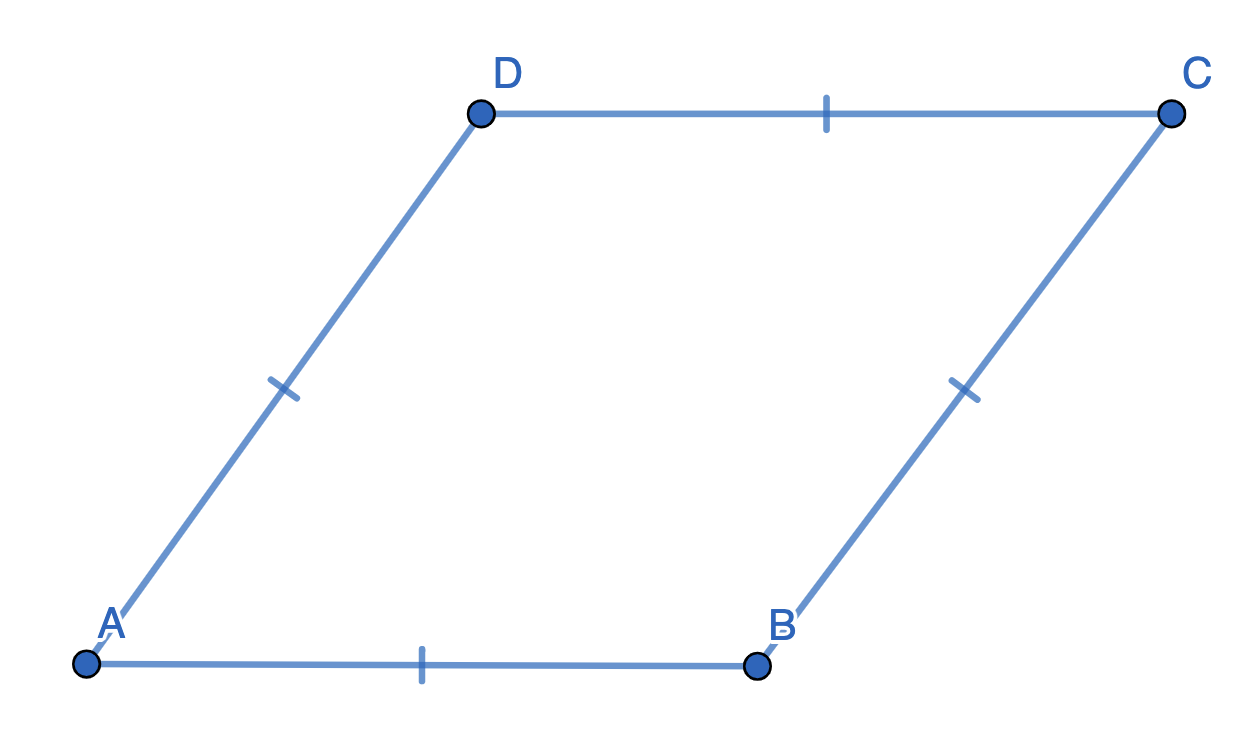
Rombos rombo ilustración StudySmarter

Ilustración de un rombo - StudySmarter Originals

A partir de la figura de ABCD, tenemos:

$A B = B C = C D = D A$

Como un rombo es un tipo de paralelogramo, los lados opuestos son paralelos. Por tanto $A D$ es paralelo a $B C$ y $A B$ es paralelo a $B C$ .

Propiedades de los rombos

Ahora que ya hemos hablado de las características básicas de un rombo, vamos a considerar sus propiedades con más detalle.

Los rombos como paralelogramos

Hemos mencionado que los rombos son un tipo especial de paralelogramo, por lo que podemos decir que todas las propiedades de los paralelogramos se aplican también a los rombos. Veamos cómo las propiedades de los paralelogramos en general se aplican específicamente a los rombos:

Los dos pares de lados opuestos de un rombo son paralelos.
Los ángulos opuestos de un rombo son iguales.
Las diagonales de un rombo se bisecan entre sí. En otras palabras, la intersección de las dos diagonales está en el punto medio de cada diagonal.
Cada diagonal de un rombo divide al rombo en 2 triángulos congruentes.

Propiedades exclusivas de los rombos

Además de las propiedades relativas a los paralelogramos, existen otras propiedades específicas y exclusivas de los rombos. A continuación las describiremos con referencia al rombo ABCD:

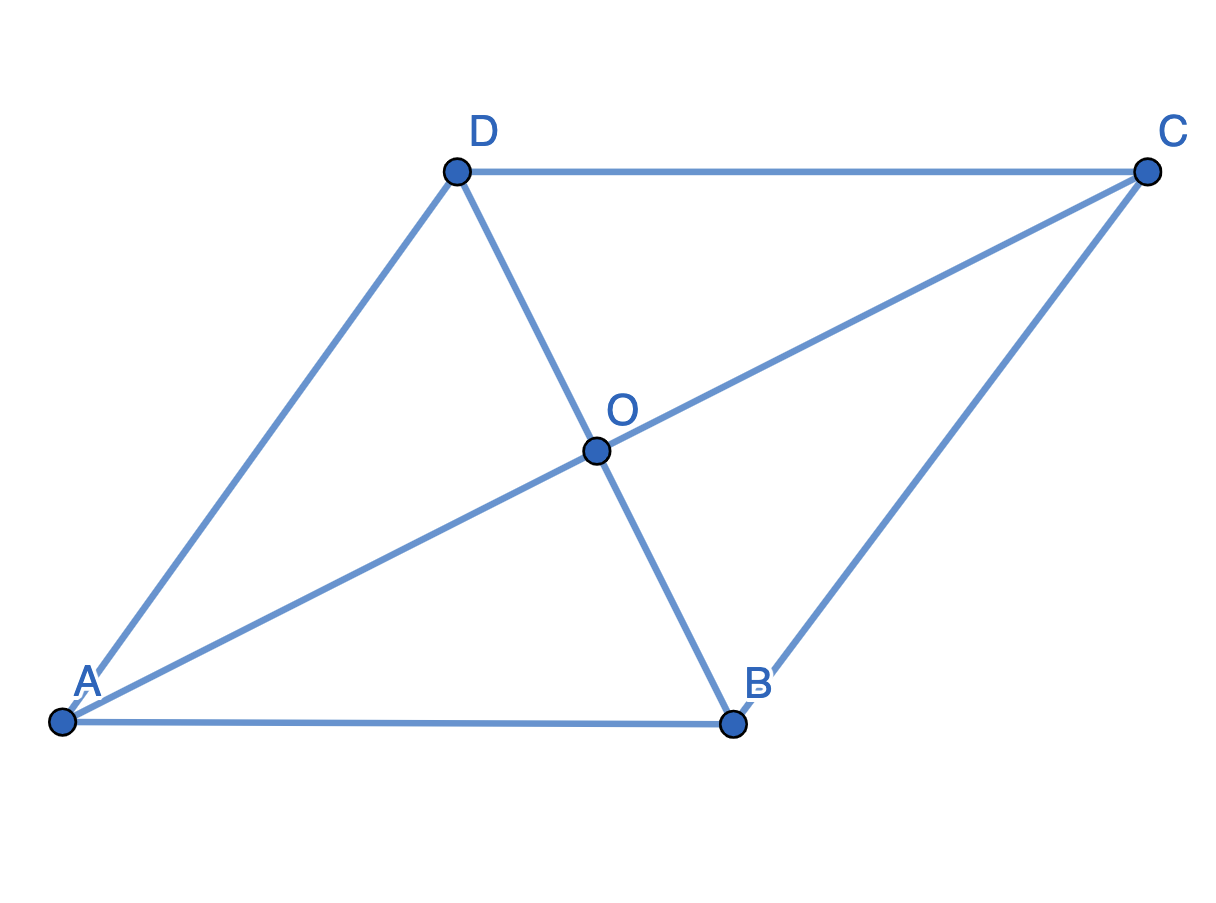
Ilustración de rombos con diagonales StudySmarter

Ilustración del rombo con diagonales - StudySmarter Originals

Las diagonales de un rombo son perpendiculares entre sí. Esto significa que son perpendiculares entre sí.
Así, en el diagrama anterior $A C ⊥ B D$ .
A partir de esto, también podríamos decir que $∠ A O D = ∠ C O D = ∠ C O B = ∠ A O B = 90 °$
Cada diagonal de un rombo biseca un par de ángulos interiores opuestos.
En otras palabras $∠ C A B = ∠ C A D = ∠ A C B = ∠ A C D$ y $∠ A B D = ∠ C B D = ∠ A D B = ∠ C D B$
Los cuatro triángulos creados al sumar las diagonales de los rombos son congruentes. Por tanto, son matemáticamente idénticos, pero sólo están orientados de forma diferente.

Los triángulos congruentes de los rombos

Por las propiedades de los rombos, sabemos que sus diagonales dividen la forma en cuatro triángulos que son congruentes. ¿Qué significa que los triángulos sean congruentes? Dos o más triángulos son congruentes si son matemáticamente idénticos. En otras palabras, todos los lados y ángulos son iguales, aunque tengan orientaciones distintas. Recuerda también que los ángulos internos de un triángulo suman 180 grados.

Considera el rombo siguiente. Demuestra que para el rombo dado, AC ⊥ BD.

El símbolo matemático ⊥ significa "perpendicular a".

Ilustración de rombos con diagonales mostradas StudySmarter

Ejemplo de rombo - StudySmarter Originals

Solución:

Por la definición de rombo:

$A B = B C = C D = D A$

Considera ahora los triángulos $A O B$ y $C O B$ :

El lado $O B$ es un lado de ambos triángulos. Ahora bien, $A B = B C$ ya que $A B C D$ es un rombo. También tenemos $O A = O C$ ya que $A B C D$ también es un paralelogramo y las diagonales de un paralelogramo se bisecan entre sí. Por tanto, el triángulo $A O B$ es congruente con el triángulo $C O B$ . En otras palabras, son exactamente los mismos triángulos, sólo que girados en posiciones distintas.

Esto implica que:

$∠ A O B = ∠ C O B$

Además $∠ A O B$ y $∠ C O B$ se encuentran en la misma recta. Por tanto,

$∠ A O B + ∠ C O B = 180 °$

por tanto,

$∠ A O B = ∠ C O B = 180 \div 2 = 90 °$

Análogamente podemos demostrar que

$∠ A O D = ∠ C O D = 90 °$

Por tanto $A C$ y $B D$ son perpendiculares. Es decir $A C ⊥ B D$ .

Fórmula del área de los rombos

Disponemos de una fórmula específica para hallar el área de un rombo. Considera el siguiente rombo:

Ilustración de rombos con diagonales mostradas StudySmarter

Ejemplo de rombo - StudySmarter Originals

Ahora, marquemos las diagonales de modo que $B D = d_{1}$ y $A C = d_{2}$ .

El área del rombo viene dada por la fórmula:

$A r e a = \frac{1}{2} d_{1} d_{2}$

Como un rombo es un tipo de cuadrilátero, también tenemos una fórmula alternativa para hallar el área.

El área de cualquier cuadrilátero viene dada por la fórmula:

$A r e a = b a s e \times h e i g h t$

Así pues, dependiendo de las longitudes que tengamos, podemos utilizar cualquiera de las fórmulas anteriores para calcular el área de un rombo.

Ten en cuenta que cuando hablamos de área, utilizamos unidades cuadradas. Por ejemplo, si las longitudes de la base y la altura se dan ambas en centímetros, las unidades del área son centímetros al cuadrado ( $c m^{2}$ ).

Un rombo tiene diagonales de longitudes $10 c m$ y $15 c m$ . ¿Cuál es el área del rombo?

Solución:

Utilizando la fórmula específica del área de un rombo, tenemos:

$A r e a = \frac{1}{2} d_{1} d_{2}$

Sustituyendo $d_{1} = 10$ y $d_{2} = 15$ tenemos:

$Area = \frac{1}{2} \times 10 c m \times 15 c m = 75 c m^{2}$

Por tanto, el área de este rombo es $75 c m^{2}$ .

Más ejemplos de rombos

Ahora veremos otros problemas de ejemplo sobre rombos.

Considera el siguiente rombo. Dado que $∠ A C B = 35 °$ $∠ D B A$ halla .

Ejemplo de rombo - StudySmarter Originals

Solución:

Recuerda que en un rombo, cada diagonal es bisectriz, lo que significa que tenemos un par de ángulos iguales. También sabemos que los ángulos opuestos en un rombo son iguales.

Por tanto,

$∠ A C B = ∠ O A B = 35 °$

Ahora bien, antes hemos dicho que las diagonales de un rombo son perpendiculares entre sí. Por tanto,

$∠ A O B = 90 °$

Puesto que $O A B$ forma un triángulo, y los ángulos de un triángulo suman $180 °$ podemos calcular $∠ D B A$ :

$∠ D B A + ∠ A O B + ∠ O A B = 180 °$

Así pues, sustituyendo los ángulos conocidos, tenemos

$∠ D B A + 90 ° + 35 ° = 180 °$

lo que implica que

$∠ D B A + 125 ° = 180 °$

Restando $180 °$ de ambos lados, obtenemos

$∠ D B A = 180 ° - 125 ° = 55 °$

Por tanto, tenemos que $∠ D B A = 55 °$ .

Considera el siguiente rombo representado a continuación. Dado que $∠ A D C = 120 °$ halla $∠ O A D$ .

Ejemplo de rombo - StudySmarter Originals

Solución:

Recuerda que la diagonal $B D$ biseca $∠ A D C$ . Por tanto, tenemos

$∠ A D O = 120 ° \div 2 = 60 °$ .

También tenemos que $∠ D O A = 90 °$ debido a la bisectriz perpendicular.

Entonces, como los ángulos de un triángulo suman $180 °$ tenemos:

$∠ O A D = 180 ° - 90 ° - 60 ° = 30 °$ .

Por tanto, $∠ O A D = 30 °$ .

Rombos - Puntos clave

Un rombo es un cuadrilátero especial con los cuatro lados de igual longitud y dos pares de lados paralelos.
Un paralelogramo es cualquier cuadrilátero con dos pares de lados paralelos, por lo que un rombo también es un paralelogramo.
Los ángulos opuestos de un rombo son iguales.
Las diagonales de un rombo se bisecan entre sí. En otras palabras, la intersección de las dos diagonales está en el punto medio de cada diagonal.
Las diagonales de un rombo dividen la forma en cuatro triángulos rectángulos congruentes.
El área de un rombo viene dada por $\frac{1}{2} d_{1} d_{2}$ donde $d_{1}$ y $d_{2}$ son las diagonales.

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Rombos

¿Qué es un rombo?

Un rombo es un cuadrilátero con cuatro lados de igual longitud donde los lados opuestos son paralelos y los ángulos opuestos son iguales.

¿Cuáles son las propiedades de un rombo?

Las propiedades de un rombo incluyen lados iguales, ángulos opuestos iguales y diagonales que se bisecan perpendicularmente.

¿Cómo se calcula el área de un rombo?

El área de un rombo se calcula multiplicando la longitud de sus diagonales y dividiendo el resultado entre dos: Área = (D1 x D2) / 2.

¿Cuál es la diferencia entre un rombo y un cuadrado?

Un rombo tiene lados iguales pero no necesariamente ángulos rectos, mientras que un cuadrado tiene todos los lados y ángulos iguales (90 grados).

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 7 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Rombos

Equipo editorial StudySmarter

Significado de los rombos