¿Cuáles son las fórmulas de las secciones cónicas?

Circunferencia (x-h)^2+(y-k)^2=r^2.Parábola ax^2+bx+c=d.Elipse (x^2)/a+(y^2)/b=1.Hipérbola ((y−k)^2)/(b^2)−((x−h)^2)/(a^2)=1.

¿Cómo se clasifican las secciones cónicas?

Cónicas degeneradas.Cónicas no degeneradas.

Secciones cónicas

Q: ¿Qué son las secciones cónicas y cómo se obtienen?

Una sección cónica es una figura geométrica generada al cortar un plano con un cono de tres dimensiones. Se pueden obtener diversas secciones, dependiendo del tipo de corte que se hace: si este es paralelo —por ejemplo— al eje de simetría, se obtiene una parábola.

Q: ¿Qué es la superficie de una cónica?

La superficie de una cónica es la superficie formada por el corte de un cono y un plano.

Q: ¿Cómo se obtiene una superficie cónica?

Una superficie cónica se obtiene al hacer girar una recta generatriz alrededor de un eje, al cual corta en un punto llamado vértice.

Análisis matemático

Estadística y probabilidad

Geometría

Matemáticas aplicadas a las ciencias sociales

Números y álgebra

Razonamiento matemático

ÍNDICE DE TEMAS :

ÍNDICE DE TEMAS

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Jetzt kostenlos anmelden

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Jetzt kostenlos anmelden

Seguro que sabes lo que es un cono: una figura geométrica, en tres dimensiones, que se parece a una pirámide cuya superficie es circular. También podemos decir, simplemente, que es como un cono de helado; es probable que esto sea más fácil de relacionar.

Un cono, de hecho, es una figura que se genera con una recta inclinada, cuando esta se pone a girar. Esta recta inclinada se denomina la generatriz.

Podrás ver imágenes de un cono en los siguientes párrafos.

Generatriz

Se denomina generatriz a la curva o línea, que al rotar, genera una figura geométrica. En el caso de las secciones cónicas, la generatriz está dada por una línea recta con cierta inclinación.

Puedes verla en la siguiente gráfica:

Secciones cónicas recta generatriz y=x StudySmarter Fig. 1: recta generatriz, donde \(y=x\).

Si esta línea (por ejemplo) se rota \(180º\), se obtiene la segunda línea:

Secciones cónicas recta generatriz y=-x StudySmarter Fig. 2: recta generatriz donde \(y=-x\).

Por último, en tres dimensiones, tendríamos una rotación como la que se ve a continuación:

Secciones cónicas rectas rotación 180 grados StudySmarter Fig. 3: recta generatriz rotada \(180\) grados.

Ahora, si esta se hace rotar alrededor de una recta vertical fija, con la que corta en un punto llamado vértice, genera algo que en análisis también se denomina como sólido de revolución; en este caso, un cono.

Secciones cónicas recta formación de cono StudySmarter Fig. 4: recta generatriz formando un cono.

Una característica del cono es que su eje divide lados opuestos de la recta en ángulos iguales.

Puedes ver esto en la figura 5:

Secciones cónicas ángulo cono StudySmarter Fig. 5: El eje del cono divide las rectas generatrices opuestas con ángulos iguales.

Superficie cónica

Una superficie cónica se obtiene cuando se hace girar una recta generatriz alrededor de un eje, al cual corta en un punto llamado vértice.

El resultado de esta revolución es una superficie en forma de cono doble —es decir, dos conos que se tocan por el vértice—, que hace que los conos sean simétricos entre sí. Hay varias figuras geométricas que se pueden obtener a partir de una superficie cónica; estas son llamadas, simplemente, cónicas.

La intersección de un plano con el cono es lo que genera estas cónicas. Hay dos tipos de ellas:

Cónicas degeneradas.
Cónicas no degeneradas.

La diferencia entre ambas radica en que para las cónicas degeneradas el plano que comparte el cono pasa por el vértice de ambos conos. Esto, en lugar de generar curvas, genera rectas o puntos.

Cónicas no degeneradas

Esencialmente hay cuatro cónicas no degeneradas, que son:

La circunferencia.
La parábola.
La elipse.
La hipérbola.

La circunferencia

Esta cónica nace de cortar el cono con un plano para formar un ángulo de \(90º\) entre el plano y el eje del cono.

Secciones cónicas circunferencia StudySmarter Fig. 6: Plano cortando un cono perpendicularmente y creando una circunferencia

La parábola

Esta sección nace de interceptar el cono con un plano paralelo a una generatriz del cono, pero cortando solo una de las hojas del cono (es decir, sin pasar por el vértice).

Secciones cónicas la parábola StudySmarter Fig. 7: Plano cortando un cono paralelo a su eje y creando una parábola

La elipse

La elipse se podría definir como un círculo, pero achatado; mientras más achatado, se dice que su excentricidad es mayor.

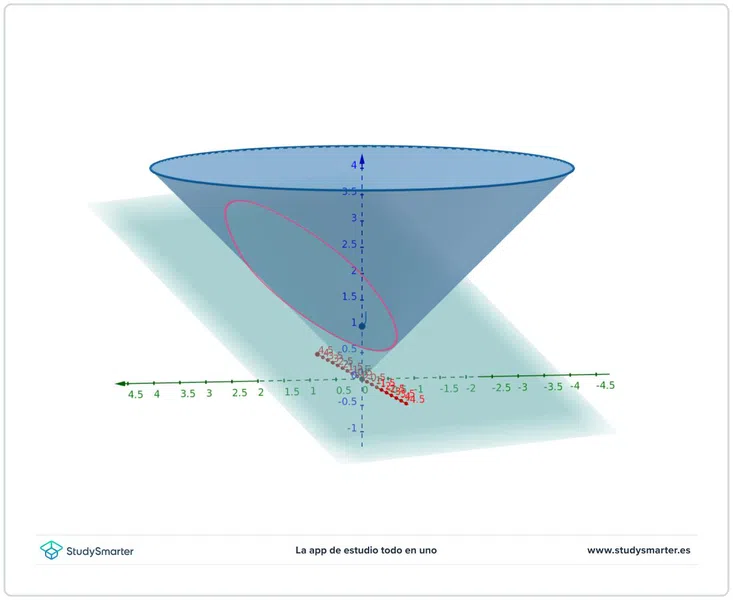
Secciones cónicas la elipse StudySmarter

Fig. 7: Plano cortando un cono, con cierta inclinación con respecto a su eje, y creando una elipse.

La excentricidad es un valor que se encuentra entre \(0<x<1\); de hecho, en caso de ser \(x=1\), lo que se tiene es un círculo.

La hipérbola

La hipérbola es la cónica que se obtiene cuando un plano corta al cono, formando un ángulo con el eje menor que el de las generatrices; por tanto, corta las dos hojas de la superficie cónica.

Secciones cónicas la hiperbola StudySmarter Fig. 8: Plano cortando dos conos y creando una hipérbola.

Cónicas degeneradas

Las cónicas degeneradas, por otro lado, son objetos que se obtienen cuando el plano corta la superficie cónica pasando por el vértice. De este modo, se obtienen tres cónicas degeneradas:

El punto: cuando el plano corta al cono por el vértice, formando un ángulo con el eje mayor que el de las generatrices.
Una recta: cuando el plano corta al cono por el vértice, formando el mismo ángulo con el eje que el de las generatrices.
Dos rectas secantes: cuando el plano corta al cono por el vértice, formando un ángulo con el eje menor que el de las generatrices.

En la figura 9 puedes observar el corte del plano con el cono por el vértice. Así se forma un ángulo entre el plano y el eje que es mayor que el ángulo entre el eje y las generatrices. Con esto se obtiene un punto, que es justamente el vértice.

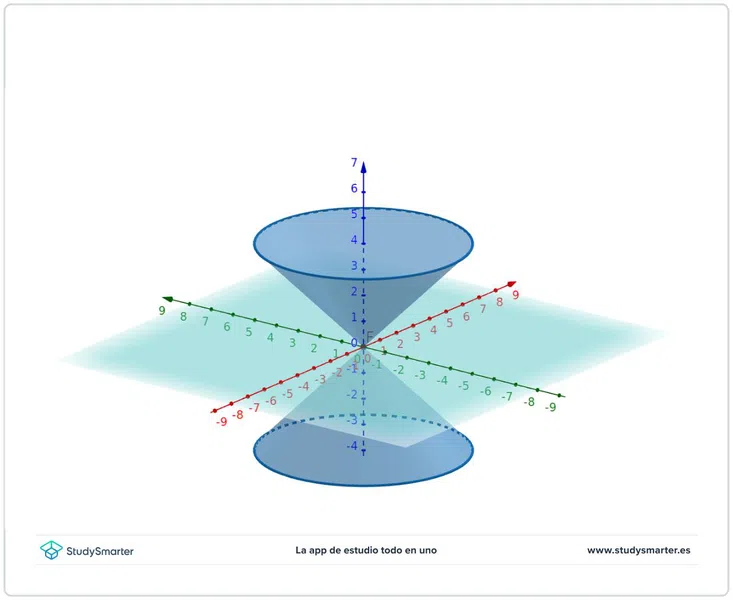
Secciones cónicas el punto StudySmarter

Fig. 9: Plano cortando el punto donde se encuentra un cono doble, creando así un punto.

Secciones cónicas - Puntos clave

Se denomina generatriz a la curva o línea que, al rotar, genera una figura geométrica.
Al rotar una generatriz, formada por una recta con una pendiente, se obtiene una superficie cónica.
El cono, al ser cortado por un plano, puede generar lo que se denomina superficies cónicas. Estas son:
- Degeneradas.
- No degeneradas.
Las cónicas degeneradas consisten en líneas y puntos.
Las cónicas no degeneradas son:
- La parábola.
- La elipse.
- La circunferencia.
- La hipérbola.

Preguntas frecuentes sobre Secciones cónicas

Una sección cónica es una figura geométrica generada al cortar un plano con un cono de tres dimensiones. Se pueden obtener diversas secciones, dependiendo del tipo de corte que se hace: si este es paralelo —por ejemplo— al eje de simetría, se obtiene una parábola.

Circunferencia (x-h)^2+(y-k)^2=r^2.
Parábola ax^2+bx+c=d.
Elipse (x^2)/a+(y^2)/b=1.
Hipérbola ((y−k)^2)/(b^2)−((x−h)^2)/(a^2)=1.

Cónicas degeneradas.
Cónicas no degeneradas.

La superficie de una cónica es la superficie formada por el corte de un cono y un plano.

Una superficie cónica se obtiene al hacer girar una recta generatriz alrededor de un eje, al cual corta en un punto llamado vértice.

Cuestionario final de Secciones cónicas

Secciones cónicas Quiz - Teste dein Wissen

Pregunta

¿Qué es una generatriz?

Mostrar respuesta

Answer

Definición: Una recta que se usa para generar un sólido al rotarla.

Show question

Pregunta

¿Se puede usar la recta \(y=x\) como una generatriz?

Mostrar respuesta

Answer

Sí.

Show question

Pregunta

¿Se puede usar la recta \(y=-x\) como una generatriz?

Mostrar respuesta

Answer

Sí.

Show question

Pregunta

Si se rota una recta con cierta inclinación sobre el origen, ¿qué figura geométrica se genera?

Mostrar respuesta

Answer

Un cono.

Show question

Pregunta

¿Qué es una sección cónica?

Mostrar respuesta

Answer

Una recta que corta un plano.

Show question

Pregunta

¿Cuáles son los dos tipos de cónicas?

Mostrar respuesta

Answer

No degeneradas y degeneradas.

Show question

Pregunta

¿La circunferencia es una sección cónica degenerada?

Mostrar respuesta

Answer

No, no lo es.

Show question

Pregunta

¿La elipse es una sección cónica degenerada?

Mostrar respuesta

Answer

No, no lo es.

Show question

Pregunta

¿Es el punto una sección cónica degenerada?

Mostrar respuesta

Answer

Sí, sí lo es.

Show question

Pregunta

¿Cuáles son las cuatro secciones cónicas no degeneradas?

Mostrar respuesta

Answer

Parábola.
Elipse.
Circunferencia.
Hipérbola.

Show question

Pregunta

¿Cómo se forma una parábola?

Mostrar respuesta

Answer

Cuando el plano corta al cono, formando un ángulo con el eje mayor que con una generatriz, pasando por el vértice.

Show question

Pregunta

¿Cuál es la ecuación de la circunferencia?

Mostrar respuesta

Answer

\[(x-h)^2+(y-k)^2=r^2\].

Show question

Pregunta

¿Cuál es la ecuación de la circunferencia con centro en el origen?

Mostrar respuesta

Answer

\((x)^2+(y)^2=r^2\).

Show question

Pregunta

¿Cuál es la ecuación de la elipse?

Mostrar respuesta

Answer

\(\dfrac{x^2}{a}+\dfrac{y^2}{b}=1\).

Show question

Pregunta

¿Cuál es la ecuación de la parábola?

Mostrar respuesta

Answer

\(ax^2+bx+c=d\).

Show question

Conoce más sobre Secciones cónicas

Resúmenes

Flashcards

Secciones cónicas

Secciones cónicas

Generatriz