Teoremas de proporcionalidad: 'reglas', 'ejemplos'

Saltar a un capítulo clave

¿Qué son los teoremas de proporcionalidad en Geometría?

Los teoremas de proporcionalidad muestran relaciones entre formas en forma de razones. Muestran cómo diferentes razones de una figura o una cantidad son iguales. Los teoremas de proporcionalidad se utilizan sobre todo en triángulos. Veamos el concepto fundamental del teorema de proporcionalidad utilizando las siguientes figuras de triángulos.

Teoremas de proporcionalidad Triángulos semejantes StudySmarter Triángulos semejantes - StudySmarter Originals

Los triángulos anteriores se llamarán triángulos semejantes si sus ángulos son congruentes y si sus lados correspondientes son proporcionales. Por tanto, la fórmula de proporcionalidad para triángulos semejantes es la siguiente.

$\frac{A B}{K L} = \frac{A C}{K M} = \frac{B C}{L M}$

¿Qué es el Teorema Básico de Proporcionalidad?

El Teorema Básico de Proporcionalidadse centra en mostrar la relación entre la longitud de los lados de un triángulo.

El teorema de proporcionalidad afirma que si se traza una línea paralela a uno de los lados de un triángulo para que corte a los otros dos lados en puntos distintos, entonces los otros dos lados se dividen en la misma proporción.

La figura siguiente ofrece una representación visual del teorema.

Teoremas de proporcionalidad Triángulo StudySmarter Un triángulo - StudySmarter Originals

En la figura $∆ A B C$ anterior, $\bar{D E}$ es paralelo a $\bar{B C}$ . Según el Teorema Básico de la Proporcionalidad, la razón de $\bar{A D}$ a $D B$ es igual a la relación de $\bar{A E}$ a $E C$ :

\frac{A D}{D B} = \frac{A E}{E C}

La relación anterior se considera la fórmula básica de proporcionalidad.

Podemos demostrar este teorema y averiguar cómo obtener la fórmula. Veamos cómo.

Por el teorema, sabemos que $D B$ y $E C$ están en la misma proporción y queremos demostrar que son iguales. Primero formaremos triángulos que tengan $D B$ y $E C$ como longitudes de sus lados. Para obtener estos triángulos, trazaremos un segmento que una $B$ a $E$ y otro segmento que una $C$ a $D$ como se muestra a continuación.

Teoremas de proporcionalidad Triángulo dividido por segmentos StudySmarter Un triángulo dividido en partes con segmentos - StudySmarter Originals

Ahora hemos formado dos nuevos triángulos $(∆ D E B a n d ∆ D E C)$ .

Lo siguiente es encontrar una relación entre los nuevos triángulos. En concreto, vamos a fijarnos en el área. $∆ D E B a n d ∆ D E C$ tienen la misma base $\bar{D E}$ y la misma altura porque el tercer vértice del triángulo está entre las mismas paralelas. Por tanto, el área de ambos triángulos debe ser igual:

A r e a_{(∆ D E B)} = A r e a_{(∆ E D C)}

Ahora, considera $∆ A E D$ . Tomemos $A D$ como base y la altura como la distancia perpendicular desde la recta $A D$ al vértice opuesto $E$ . Mira cómo queda en la siguiente figura.

Teoremas de proporcionalidad Triángulo dividido por segmentos StudySmarter Un triángulo dividido en partes con segmentos - StudySmarter Originals

El área de este triángulo es

A r e a_{(∆ A E D)} = \frac{1}{2} \times \bar{A D} \times \bar{E P}

También necesitamos el área de $∆ D E B$ que será:

A r e a_{(∆ D E B)} = \frac{1}{2} \times \bar{D B} \times \bar{E P}

Ahora, podemos tomar el cociente entre el área de $∆ D E B$ y el área de $∆ A E D$ y compararla con la relación entre el área de $∆ E C D$ y el área de $∆ A E D$ . Por tanto, la razón de las áreas es :

$\frac{a r (∆ A E D)}{a r (∆ D E B)} = \frac{\frac{1}{2} \times A D \times E P}{\frac{1}{2} \times D B \times E P} = \frac{A D}{D B}$

Como ves, ya tenemos la primera parte de la fórmula. Para obtener la otra, repetiremos todo lo que acabamos de hacer pero con $∆ E D C$ .

A diferencia de antes, en lugar de utilizar $A D$ como base de $∆ A E D$ utilizaremos $A E$ como base y la altura será la distancia perpendicular opuesta al vértice $D$ . Mira cómo queda en la siguiente figura.

Teoremas de proporcionalidad Triángulo dividido por segmentos StudySmarter Un triángulo dividido en partes con segmentos - StudySmarter Originals

El área de $∆ A E D$ según la imagen anterior es

$A r e a_{(∆ A E D)} = \frac{1}{2} \times \bar{A E} \times \bar{D Q}$

Consideremos ahora el área de $∆ E D C$ . Tomaremos EC como base y $D Q$ como altura. El área es la siguiente.

$A r e a_{(∆ E D C)} = \frac{1}{2} \times \bar{E C} \times \bar{D Q}$

Ahora obtendremos que el cociente de ambas áreas es :

$\frac{A r e a_{(∆ A E D)}}{A r e a_{(∆ E D C)}} = \frac{\frac{1}{2} \times A E \times D Q}{\frac{1}{2} \times E C \times D Q} = \frac{A E}{E C}$

Ya ves que hemos obtenido la otra parte de la fórmula. Pero, ¿cómo demostramos que ambas partes son iguales? Igualemos ambas proporciones y veremos.

$\frac{A r e a_{(∆ A E D)}}{A r e a_{(∆ D E B)}} = \frac{A r e a_{(∆ A E D)}}{A r e a_{(∆ E D C)}}$

Ambos numeradores son iguales, por lo que son iguales. Recuerda que al principio de la demostración vimos que

A r e a_{(∆ D E B)} = A r e a_{(∆ E D C)}

Por tanto

\frac{A D}{D B} = \frac{A E}{E C}

El Teorema de la Proporcionalidad de los Triángulos y el Teorema Fundamental de la Proporcionalidad

El Teorema de la Proporcionalidad Triangular y el Teorema Fundamental de la Proporcionalidad sonotros nombres del Teorema Básico de la Proporcionalidad. Puedes ver este teorema con cualquiera de estos nombres.

Teorema de proporcionalidad Ejemplos

Veamos la aplicación del teorema de proporcionalidad con algunos ejemplos.

Considera un $∆ A B C$ donde DE es paralela a $B C$ . $A D = 1.5 c m, D B = 3 c m, A E = 1$ . Encuentra $E C$ .

Recuerda la fórmula

\frac{A D}{D B} = \frac{A E}{E C}

Sólo tenemos que sustituir los valores.

$\frac{1.5}{3} = \frac{1}{E C} 1.5 \times E C = 3 \times 1 1.5 E C = 3 E C = \frac{3}{1.5} E C = 2 c m$

Veamos otro ejemplo.

Considera $∆ E F G$ donde $H L$ y $E F$ son paralelas entre sí. $E H = 9 c m, H G = 21, F L = 6 c m$ . Encuentra $L G$

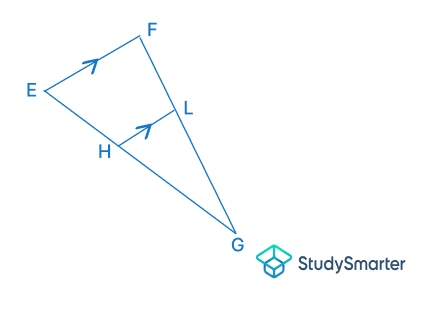
Teoremas de proporcionalidad Un ejemplo para resolver la proporcionalidad StudySmarterrtio

Según el teorema de proporcionalidad,

\frac{E H}{H G} = \frac{F L}{L G}

Sumando los valores conocidos obtenemos

$\begin{array}{rcl} \frac{9}{21} & = & \frac{6}{L G} \\ 9 \times L G & = & 6 \times 21 \\ 9 L G & = & 126 \\ L G & = & \frac{126}{9} \\ L G & = & 14 c m \end{array}$

Además de mostrar la relación entre la longitud de los lados de los triángulos, en la vida real, el teorema de proporcionalidad puede utilizarse en la construcción.

La inversa del teorema básico de proporcionalidad

La inversa del teorema básico de proporcionalidad es la inversa del teorema básico de proporcionalidad. El teorema afirma que si se traza una recta que corte a dos lados de un triángulo en puntos distintos de modo que corte a los dos lados en la misma proporción, entonces la recta es paralela al tercer lado.

Teoremas de proporcionalidad Teorema de proporcionalidad del triángulo StudySmarter Un Triángulo - StudySmarter Originals

En el teorema básico de proporcionalidad, vimos que $D E$ y $B C$ son paralelas y ahora queremos demostrar que $D E$ y $B C$ son efectivamente paralelas. Lo haríamos utilizando el teorema básico de proporcionalidad, que es

\frac{A D}{D B} = \frac{A E}{E C}

Esta prueba es una prueba por contradicción, lo que significa que supondremos que nuestro resultado deseado es erróneo. Supondremos que $D E$ no es paralela a $B C$ ( $(D E ∦ B C)$ . Si es así, debe haber otro punto de la recta $A C$ tal que un segmento trazado desde el punto $D$ a ese punto sea paralelo a $B C$ . Observa la siguiente figura para mayor claridad.

Teoremas de proporcionalidad Teorema de proporcionalidad inversa StudySmarter Un triángulo dividido en partes con segmentos - StudySmarter Originals

Ahora que tenemos un segmento de recta $A F$ que es paralelo a $B C$ podemos utilizar el teorema básico de proporcionalidad, que es

$\frac{A D}{D B} = \frac{A F}{F C}$

Si consideras el teorema básico de proporcionalidad, tendrás:

$\frac{A D}{D B} = \frac{A F}{F C} = \frac{A E}{E C}$

Ahora hemos deducido que $D F$ es paralela a $B C$ y queremos demostrar que $D E$ es paralela a $B C$ . Esto significa que lo que realmente queremos hacer es demostrar que $D F$ y $D E$ son los mismos segmentos. Por tanto, si consideramos la ecuación anterior, verás que la primera razón no es realmente necesaria. Así que nos queda

$\frac{A F}{F C} = \frac{A E}{E C}$

Ahora decimos que $D F$ y $D E$ son los mismos segmentos, lo que significa que el punto $F$ y el punto $E$ son iguales. Si ésta es nuestra conclusión, entonces el segmento $A F$ y $A E$ son iguales, pero aún no lo hemos demostrado.

A partir de la figura, podemos decir que el segmento $A C$ es igual a la suma del segmento $A E$ y $E C$ .

$A C = A E + E C$

Volvamos a una de nuestras ecuaciones.

\frac{A F}{F C} = \frac{A E}{E C}

Ahora añadiremos 1 ( uno) a ambos lados de la ecuación y los llevaremos a las fracciones dándoles un denominador común.

$\begin{array}{rcl} \frac{A F}{F C} + 1 & = & \frac{A E}{E C} + 1 \\ \frac{A F}{F C} + \frac{F C}{F C} & = & \frac{A E}{E C} + \frac{E C}{E C} \\ \frac{A F + F C}{F C} & = & \frac{A E + E C}{E C} \end{array}$

Los dos numeradores de ambos lados de la ecuación son representaciones del segmento $A C$ . Por tanto, podemos sustituirlos por $A C$

$\frac{A C}{F C} = \frac{A C}{E C}$

Simplifiquemos aún más multiplicando ambos lados por $\frac{1}{A C}$ .

$\begin{array}{rcl} \frac{A C}{F C} \times \frac{1}{A C} & = & \frac{A C}{E C} \times \frac{1}{A C} \\ \frac{1}{F C} & = & \frac{1}{E C} \end{array}$

Como son iguales, sus recíprocos también lo serán. Por tanto,

$\bar{F C} = \bar{E C}$

Debes observar que $F C$ y $E C$ están en la misma recta. Si están en la misma recta, la única forma de que sean iguales es que ambos segmentos partan del mismo punto. Esto significa que el punto F debe ser igual al punto $E$ . También significa que el segmento $D E$ es igual a $D F$ .

Esto concluye que $D F$ es efectivamente paralelo a $B C$ .

Teoremas de proporcionalidad - Puntos clave

El teorema básico de proporcionalidad afirma que si se traza una recta paralela a un lado de un triángulo para que corte a los otros dos lados en puntos distintos, entonces los otros dos lados se dividen en la misma proporción. La figura siguiente ofrece una representación visual del teorema.
El teorema básico de proporcionalidad también se conoce como teorema de proporcionalidad del triángulo y teorema del segmento de proporcionalidad.
La inversa del teorema básico de proporcionalidad es la inversa del teorema básico de proporcionalidad. El teorema afirma que si se traza una recta que corte a dos lados de un triángulo en puntos distintos de forma que corte a los dos lados en la misma proporción, entonces la recta es paralela al tercer lado.

Tarjetas en Teoremas de proporcionalidad 4

Empieza a aprender

El teorema básico de proporcionalidad también se llama teorema de proporcionalidad triangular.

Verdadero

El teorema de proporcionalidad inverso es la inversa del teorema de proporcionalidad básico.

Verdadero

El teorema de la proporcionalidad puede utilizarse en la construcción. Verdadero o Falso

Verdadero

El teorema de proporcionalidad se utiliza para mostrar la relación entre la longitud de los lados de los triángulos.

Verdadero

Aprende con 4 tarjetas de Teoremas de proporcionalidad en la aplicación StudySmarter gratis

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Teoremas de proporcionalidad

¿Qué es el Teorema de Tales?

El Teorema de Tales establece que si dos líneas son cortadas por un par de líneas paralelas, los segmentos correspondientes son proporcionales.

¿Cómo se aplica el Teorema de la Bisectriz?

El Teorema de la Bisectriz indica que la bisectriz de un ángulo en un triángulo divide el lado opuesto en segmentos proporcionales a los otros dos lados del triángulo.

¿Qué dice el Teorema de la Proporcionalidad Multiple?

El Teorema de la Proporcionalidad Múltiple afirma que si tres o más líneas paralelas son cortadas por dos transversales, los segmentos correspondientes son proporcionales.

¿Cómo se utiliza el Teorema de los Triángulos Semejantes?

El Teorema de los Triángulos Semejantes establece que dos triángulos son semejantes si sus ángulos correspondientes son iguales y sus lados proporcionales.

Guardar explicación

Pon a prueba tus conocimientos con tarjetas de opción múltiple

TU PUNTUACIÓN

Tu puntuación

¿Ya tienes una cuenta? Iniciar sesión

Puntuación

Accede a más de 700 millones de materiales de aprendizaje

Estudia de manera más eficiente con tarjetas de memoria

Mejora tus calificaciones con IA

¿Ya tienes una cuenta? Inicia sesión

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 9 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Teoremas de proporcionalidad

Equipo editorial StudySmarter

¿Qué son los teoremas de proporcionalidad en Geometría?

¿Qué es el Teorema Básico de Proporcionalidad?

El Teorema de la Proporcionalidad de los Triángulos y el Teorema Fundamental de la Proporcionalidad

Teorema de proporcionalidad Ejemplos

La inversa del teorema básico de proporcionalidad

Teoremas de proporcionalidad - Puntos clave

Tarjetas en Teoremas de proporcionalidad 4

Aprende con 4 tarjetas de Teoremas de proporcionalidad en la aplicación StudySmarter gratis

Preguntas frecuentes sobre Teoremas de proporcionalidad

Pon a prueba tus conocimientos con tarjetas de opción múltiple

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Empresa

Nuestros productos

Ponte en contacto

Teoremas de proporcionalidad

Equipo editorial StudySmarter

¿Qué son los teoremas de proporcionalidad en Geometría?

¿Qué es el Teorema Básico de Proporcionalidad?

El Teorema de la Proporcionalidad de los Triángulos y el Teorema Fundamental de la Proporcionalidad

Teorema de proporcionalidad Ejemplos

La inversa del teorema básico de proporcionalidad

Teoremas de proporcionalidad - Puntos clave

Tarjetas en Teoremas de proporcionalidad 4

Aprende con 4 tarjetas de Teoremas de proporcionalidad en la aplicación StudySmarter gratis

Preguntas frecuentes sobre Teoremas de proporcionalidad

Pon a prueba tus conocimientos con tarjetas de opción múltiple

¡Únete a la aplicación StudySmarter y aprende de manera eficiente con millones de tarjetas y mucho más!

Aprende con 4 tarjetas de Teoremas de proporcionalidad en la aplicación StudySmarter gratis

¡Fue un comienzo fantástico!

Puedes hacerlo mejor

Regístrate para crear tus propias tarjetas de memoria

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Crea una cuenta gratuita para guardar esta explicación.

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.