Semejanza y transformaciones
Al hablar de transformaciones de semejanza, hay que tener en cuenta dos términos: semejanza y transformación. Empecemos con una pequeña introducción sobre lo que significan transformación y semejanza.
Una transformación en geometría significa cambiar la posición o la forma de una figura geométrica.
La semejanza es una propiedad de las figuras geométricas cuando éstas tienen la misma forma pero distinto tamaño.
Decimos que dos figuras son semejantes cuando una puede obtenerse a partir de la otra porque la razón de sus lados correspondientes es igual. Las figuras semejantes tienen la misma forma pero distinto tamaño. Considera la siguiente figura.
 Triángulos semejantes - StudySmarter Originals
Triángulos semejantes - StudySmarter Originals
La figura anterior muestra dos triángulos de distinto tamaño. La razón de sus lados correspondientes también es igual.
Por tanto, los triángulos son semejantes. Ahora que sabemos qué son la transformación y la semejanza individualmente, veamos qué es la transformación de semejanza.
¿Qué es una transformación de semejanza?
Cuando tienes dos figuras y una de ellas se amplía o se reduce, lo llamamos transformación de semejanza.
Una transformación de semejanza es cuando una figura se transforma en otra mediante ampliación o reducción de tamaño.
La figura en la que se transforma la forma se llama imagen, mientras que la figura original se llama preimagen.
Cuando se trate de transformaciones de semejanza, necesitarás un factor de escala. Para revisar el factor de escala, ve a Volumen, Área, Longitud y Dilataciones. De este artículo, recuerda que si el factor de escala es entonces la figura se reduce. Si entonces la figura se amplía.
Cada punto se dilata a partir de un punto fijo llamado centro de dilatación. Considera la siguiente figura.
 Transformación por semejanza de un triángulo pequeño en uno mayor - StudySmarter Originals
Transformación por semejanza de un triángulo pequeño en uno mayor - StudySmarter Originals
En la figura anterior, el punto es el centro de dilatación, punto fijo utilizado cuando se trata de factores de escala. se está dilatando a lo que significa que es una ampliación porque es menor que . Si tomas la distancia de a obtendrás una fracción igual a la que obtendrías tomando la distancia de a . Esto significa que la propiedad de semejanza se mantiene a pesar de la ampliación o reducción del tamaño de la figura. Matemáticamente, escribimos
La notación primo (denotada con un apóstrofo, ' ) se utiliza a veces para distinguir el etiquetado de la imagen y la preimagen.
Veamos un ejemplo para mostrar lo que queremos decir.
Dado abajo con coordenadasun centro de dilatación y un factor de escala de 2.
Aplica la dilatación al polígono y traza .
Solución:
Paso 1: Empezaremos dibujando la imagen previa .
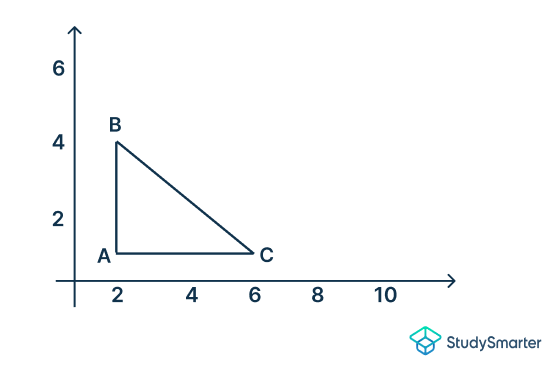
Paso 2: Por la pregunta, vemos que el factor de escala es 2. Observa que el factor de escala es mayor que 1. Esto significa que se trata de una ampliación. Por tanto, multiplica cada coordenada x e y de por el factor de escala, 2. Véase la tabla siguiente.
| (x, y) | (2x, 2y) |
| A (2, 1) | |
| B ( 2, 3) | |
| C (5, 1) | |
Paso 3: Hemos multiplicado por 2 para obtener las coordenadas de la parte derecha de la tabla anterior. Si dibujas estas nuevas coordenadas en la gráfica, obtendrás
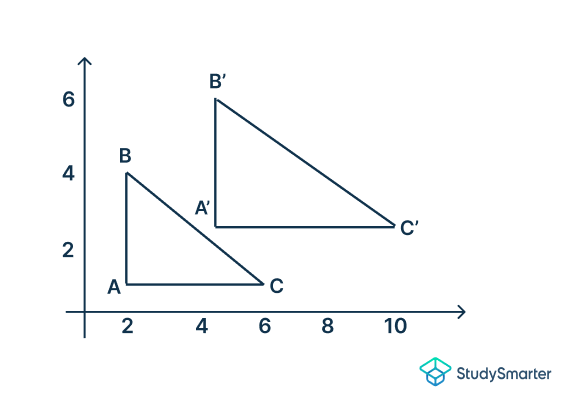
Como puedes ver
es la imagen previa que se ha transformado en la imagen
.
Propiedades de las transformaciones de semejanza
He aquí algunas propiedades de las transformaciones de semejanza.
Se producen cuando se amplía o reduce una figura para producir una imagen de la misma.
Los lados correspondientes de la imagen previa y de su imagen deben tener la misma proporción.
Las coordenadas de la figura y su imagen deben tener la misma proporción.
Existe un factor de escala . Si existe una figura la imagen de la figura será .
Encontrar transformaciones de semejanza - Ejemplos
Si el centro de dilatación es (0,0), podemos multiplicar cada coordenada x e y por el factor de escala, k, para obtener las coordenadas de la preimagen. Matemáticamente,
| Coordenada de la preimagen | Coordenada de la imagen |
| x,y | |
El centro de dilatación puede ser cualquier punto del plano cartesiano, aunque (0,0) es el más habitual en la práctica.
Veamos ahora cómo determinar si dos figuras son semejantes o no con los siguientes ejemplos.
Las figuras del gráfico siguiente muestran formas con coordenadas Determina si son semejantes o no.
Paso 1: Haz un diagrama
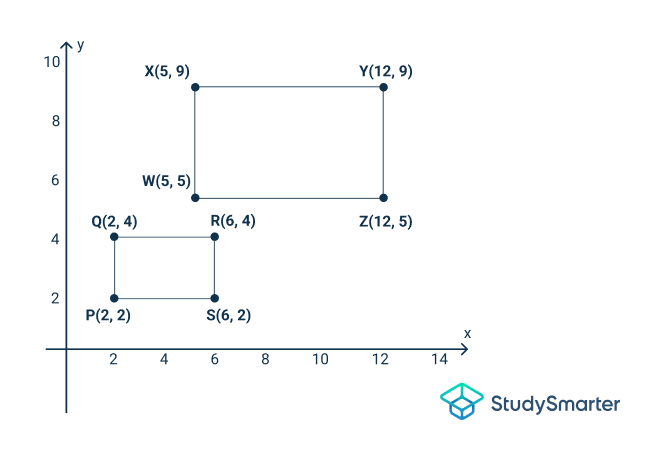
Como puedes ver en el gráfico, las figuras se han dilatado, lo que significa que se ha producido alguna transformación.
Paso 2: La forma más rápida de comprobar sus semejanzas es comparar las coordenadas de ambas figuras. La primera figura es y la segunda es . En primer lugar, tenemos que identificar los vértices correspondientes. Los rectángulos están ambos en orientación horizontal, por lo que podemos hacer coincidir la parte inferior izquierda de uno con la parte inferior izquierda del otro y así sucesivamente. Deberías obtener que P corresponde a W (ambos abajo a la izquierda), S corresponde a Z (abajo a la derecha), Q a X (arriba a la izquierda) y R a Y (arriba a la derecha).
A continuación, comprobamos
Paso 3: Introduciendo las coordenadas en la ecuación anterior, obtenemos
Como puedes ver, las coordenadas no son iguales, por lo que no existe semejanza.
Obtendrás el cociente de cada coordenada para ver si tendrán el mismo factor de escala.
El primer conjunto de coordenadas a comparar es . El cociente será . Son iguales.
El segundo conjunto es (La proporción será . Nuestro resultado no es igual, lo que significa que las cifras no pueden ser semejantes. Si hubiéramos obtenido en lugar de entonces habríamos continuado con la siguiente coordenada para ver si obteníamos otro como factor de escala. El factor de escala difiere, por lo que las figuras no son semejantes.
Otra forma de hacerlo es mirar la propia gráfica. Debes comparar los lados correspondientes de las figuras y ver si tienen la misma proporción.
A partir de la figura es 2 y es 4. La proporción aquí es que es .
es 4 y es 7. La proporción aquí es . es muy diferente de .
Por lo tanto, no existe semejanza.
Otros tipos de transformaciones de semejanza
Existen otros tipos de transformaciones en geometría, como la reflexión, la rotación y la traslación. Como se ha mencionado al principio de este artículo, puedes encontrar ejemplos relacionados con ellas en el artículo sobre Transformaciones.
Reflexiones
Se habla de reflexión cuando se da la vuelta a una figura para obtener una imagen especular.
 Imágenes reflejadas - StudySmarter Originals
Imágenes reflejadas - StudySmarter Originals
Rotaciones
Rotación es cuando la figura se gira sobre un punto fijo.
 Imágenes Giradas - StudySmarter Originals
Imágenes Giradas - StudySmarter Originals
Traslados
Trasladar es simplemente deslizar la figura por el plano.
 Imágenes traducidas - Originales de StudySmarter
Imágenes traducidas - Originales de StudySmarter
Estos tipos de transformación producen principalmente imágenes que son congruentes con las figuras originales, pero a veces pueden utilizarse cuando la similitud no puede determinarse fácilmente. Veamos cómo con los ejemplos siguientes.
Determina si las siguientes figuras son similares o no.
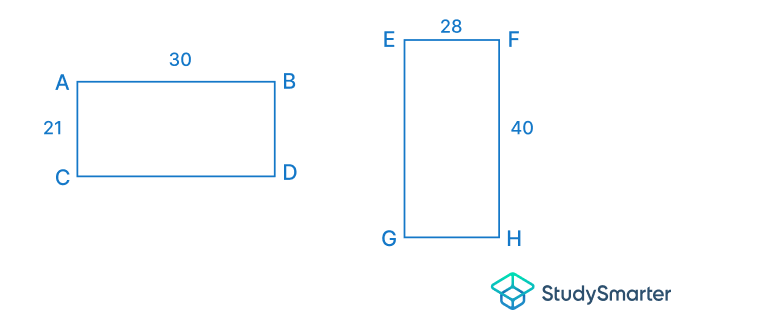
En realidad, no puedes saber si son similares con sólo mirarlas, porque están colocadas en posiciones diferentes. Vamos a rotar y luego trasladar la primera figura y ver el resultado.
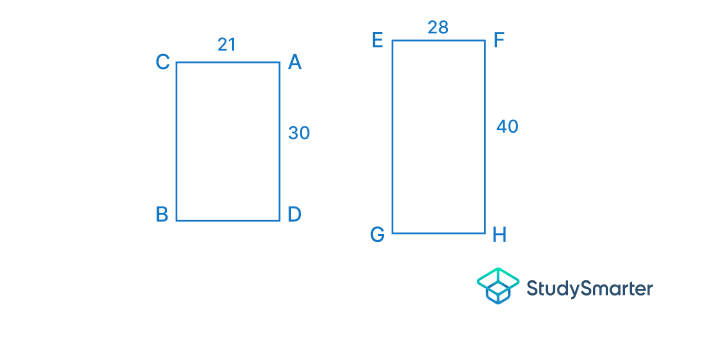
Tras girar y trasladar, se obtuvo la figura anterior. Como puedes ver, ambas están en la misma orientación y ahora puedes hacer comparaciones utilizando las partes correspondientes.
Las piezas están en la misma proporción. Por tanto, son similares.
Transformaciones de semejanza - Puntos clave
- Transformación de semejanza es cuando una figura se transforma en otra mediante dilatación. Dilatación significa ampliar y reducir el tamaño.
- Decimos que dos figuras son semejantes cuando las proporciones de sus lados correspondientes son iguales.
- La figura en la que se transforma la forma se llama imagen, y la forma original se llama preimagen.
- Si el centro de dilatación es 0, basta con multiplicar las coordenadas x e y de la imagen previa por el factor de escala para obtener las coordenadas de la nueva imagen.
- El centro de dilatación es un punto fijo a partir del cual se dilatan todos los puntos.
- Otros tipos de transformación en geometría son la reflexión, la rotación y la traslación.

















