Volumen de la Pirámide: Fórmulas, Ejemplos

Saltar a un capítulo clave

¿Qué es una pirámide?

Las pirámides son objetos tridimensionales con lados o superficies triangulares que se unen en una punta llamada vértice. El nombre "pirámide" suele evocar las Pirámides de Egipto, que son una de las siete maravillas del mundo.

En geometría, una pirámide es un poliedro obtenido uniendo una base poligonal a un punto, llamado vértice.

Tipos de pirámides

Las pirámides son de varios tipos según la forma de su base. Una pirámide de base triangular se llama pirámide triangular, y una pirámide de base rectangular se conoce como pirámide rectangular. Los lados de una pirámide son triangulares y salen de su base. Todos se unen en un punto llamado vértice.

Volumen de las pirámides Una imagen que muestra los distintos tipos de pirámides StudySmarter Una imagen que muestra los distintos tipos de pirámides, Njoku - StudySmarter Originals

¿Cuál es el volumen de una pirámide?

Quizá te preguntes cuántos bloques de arena pueden formar las pirámides egipcias. El volumen de una pirámide es el espacio encerrado por sus caras. Generalmente, el volumen de una pirámide es un tercio del de su prisma correspondiente. Su prisma correspondiente tiene la misma forma de base, dimensiones de base y altura. Por tanto, la fórmula general para calcular el volumen de una pirámide es

$V = \frac{1}{3} \times b h$

donde,

V es el volumen de la pirámide

b es el área de la base de la pirámide

h es la altura de la pirámide

Observa que ésta es la fórmula general para el volumen de todas las pirámides. Las diferencias en las fórmulas se basan en la forma de la base de la pirámide.

Volumen de las pirámides rectangulares

El volumen de las pirámides rectangulares se puede hallar multiplicando un tercio del área de la base rectangular por la altura de la pirámide. Por tanto:

$V o l u m e o f r e c \tan g u l a r p y r a m i d = \frac{1}{3} \times b a s e A r e a \times h e i g h t B a s e a r e a = l e n g t h \times b r e a d t h V o l u m e = \frac{1}{3} \times l \times b \times h$

donde

l es la longitud de la base

b es la anchura de la base

h es la altura de la pirámide

Volumen de las pirámides Ilustración de los lados de una pirámide rectangular StudySmarter Ilustración de los lados de una pirámide rectangular, Njoku - StudySmarter Originals

Esto significa que el volumen de una pirámide rectangular es un tercio del del prisma rectangular correspondiente.

Volumen de las pirámides de base cuadrada

Una pirámide de base cuadrada es una pirámide cuya base es un cuadrado. El volumen de las pirámides de base cuadrada se obtiene multiplicando un tercio del área de la base cuadrada por la altura de la pirámide. Por tanto

$V o l u m e o f s q u a r e b a s e p y r a m i d = \frac{1}{3} \times b a s e A r e a \times h e i g h t B a s e a r e a = l e n g t h^{2} V o l u m e = \frac{1}{3} \times l^{2} \times h$

donde

l es la longitud de la base cuadrada

h es la altura de la pirámide

Volumen de las pirámides Ilustración de los lados de una pirámide de base cuadrada StudySmarter Ilustración de los lados de una pirámide de base cuadrada, Njoku - StudySmarter Originals

Volumen de las pirámides de base triangular

El volumen de las pirámides de base triangular puede obtenerse multiplicando un tercio del área de la base triangular por la altura de la pirámide. Por tanto:

$V o l u m e o f t r i a n g u l a r b a s e p y r a m i d = \frac{1}{3} \times b a s e A r e a \times h e i g h t B a s e a r e a = \frac{1}{2} \times b a s e l e n g t h \times h e i g h t o f t r i a n g l e V o l u m e = \frac{1}{3} \times \frac{1}{2} \times b \times h_{t r i a n g l e} \times h_{p y r a m i d} V = \frac{1}{6} \times b \times h_{t r i a n g l e} \times h_{p y r a m i d}$

donde

l es la longitud de la base

b es la longitud de la base triangular

_htriángulo es la altura de la base triangular

_hpirámide es la altura de la pirámide

Volumen de las pirámides Ilustración de los lados de una pirámide triangular StudySmarter Ilustración de los lados de una pirámide triangular, Njoku - StudySmarter Originals

Volumen de pirámides hexagonales

El volumen de las pirámides de base hexagonal se puede obtener multiplicando un tercio del área de la base hexagonal por la altura de la pirámide. Por tanto:

$V o l u m e o f t r i a n g u l a r b a s e p y r a m i d = \frac{1}{3} \times b a s e A r e a \times h e i g h t B a s e a r e a = \frac{3 \sqrt{3}}{2} \times l e n g t h^{2} V o l u m e = \frac{1}{3} \times \frac{3 \sqrt{3}}{2} \times l^{2} \times h V o l u m e = \frac{\sqrt{3}}{2} \times l^{2} \times h$

Volumen de las pirámides Ilustración de los lados de una pirámide hexagonal StudySmarter Ilustración de los lados de una pirámide hexagonal, Njoku - StudySmarter Originals

Una pirámide de 15 pies de altura tiene una base cuadrada de 12 pies. Determina el volumen de la pirámide.

Solución

$V o l u m e o f s q u a r e b a s e p y r a m i d = \frac{1}{3} \times l^{2} \times h l = 12 f t h = 15 f t V = \frac{1}{3} \times 12^{2} \times 15 V = 5 \times 144 V = 720 f t^{3}$

Calcula el volumen de la siguiente figura:

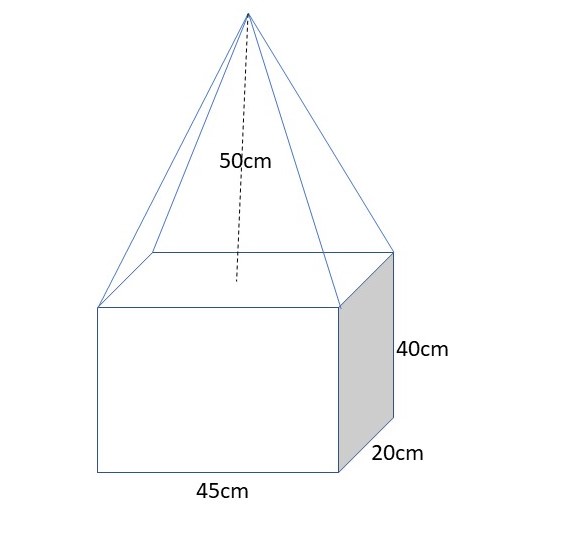
Composición de Pirámide y Cuboide

Solución

$T h e v o l u m e o f t h e f i g u r e = v o l u m e o f r e c t a n g u l a r p y r a m i d + v o l u m e o f r e c t a n g u l a r p r i s m V o l u m e o f r e c t a n g l a r p y r a m i d = \frac{1}{3} \times l \times b \times h l = 45 c m b = 20 c m h = 50 c m V o l u m e o f r e c t a n g l a r p y r a m i d = \frac{1}{3} \times 45 \times 20 \times 50 V o l u m e o f r e c t a n g l a r p y r a m i d = 15000 c m^{3} V o l u m e o f r e c t a n g u l a r p r i s m = l \times b \times h l = 45 c m b = 20 c m h = 40 c m V o l u m e o f r e c t a n g u l a r p r i s m = 45 \times 20 \times 40 V o l u m e o f r e c t a n g u l a r p r i s m = 36000 c m^{3} T h e v o l u m e o f t h e f i g u r e = v o l u m e o f r e c t a n g u l a r p y r a m i d + v o l u m e o f r e c t a n g u l a r p r i s m T h e v o l u m e o f t h e f i g u r e = 15000 + 36000 T h e v o l u m e o f t h e f i g u r e = 51000 c m^{3}$

Una pirámide hexagonal y una pirámide triangular tienen la misma capacidad. Si su base triangular tiene una longitud de 6 cm y una altura de 10 cm, calcula la longitud de cada lado del hexágono cuando ambas pirámides tengan la misma altura.

Solución

El primer paso es expresar la relación en una ecuación.

Según el problema, el volumen de la pirámide triangular es igual al volumen de la pirámide hexagonal.

Sea _bt el área de la base triangular y _bh el área de la base hexagonal.

Entonces

$V o l u m e o f t r i a n g u l a r p y r a m i d = V o l u m e o f h e x a g o n a l p y r a m i d \frac{b_{t} h}{3} = \frac{b_{h} h}{3}$

Multiplica ambos lados de la ecuación por 3 y divídelos por h.

$\frac{b_{t} h}{3} = \frac{b_{h} h}{3} \frac{b_{t} h}{3} \times \frac{3}{h} = \frac{b_{h} h}{3} \times \frac{3}{h} b_{t} = b_{h}$

Esto significa que la base triangular y la base hexagonal tienen la misma área.

Recuerda que debemos hallar la longitud de cada lado del hexágono.

$b_{t} = \frac{1}{2} \times b a s e l e n g t h \times h e i g h t b a s e l e n g t h o f t r i a n g l e = 6 c m h e i g h t o f t r i a n g l e = 10 c m b_{h} = \frac{3 \sqrt{3}}{2} \times l^{2}$

Donde l es la longitud del lado de un hexágono.

Recuerda que entonces _bt = _bh;

$\frac{1}{2} \times 6 \times 10 = \frac{3 \sqrt{3}}{2} \times l^{2} \frac{1}{2} \times 6 \times 10 \times \frac{2}{3 \sqrt{3}} = \frac{3 \sqrt{3}}{2} \times l^{2} \times \frac{2}{3 \sqrt{3}} \frac{20}{\sqrt{3}} = l^{2}$

Toma las raíces de ambos lados de la ecuación.

$\sqrt{l^{2}} = \sqrt{11.547} l = 3.398 c m$

Por tanto, cada lado de la base hexagonal mide aproximadamente 3,4 cm.

Volumen de una pirámide - Puntos clave

Una pirámide es un objeto tridimensional con lados o superficies triangulares que se unen en una punta llamada vértice
Los distintos tipos de pirámides se basan en la forma de su base
El volumen de una pirámide es un tercio del área de la base × la altura

Tarjetas en Volumen de la Pirámide 2

Empieza a aprender

¿Qué determina el tipo de pirámide?

La forma de la base

Una pirámide es un tercio de su prisma correspondiente.

Sí

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Volumen de la Pirámide

¿Cómo se calcula el volumen de una pirámide?

El volumen de una pirámide se calcula con la fórmula: V = (1/3) * B * h, donde B es el área de la base y h es la altura.

¿Qué es la base en la fórmula del volumen de una pirámide?

La base es la superficie inferior de la pirámide, generalmente una figura geométrica como un cuadrado o un triángulo.

¿Qué representa la altura en la fórmula del volumen de una pirámide?

La altura es la distancia perpendicular desde la base hasta el vértice de la pirámide.

¿La fórmula del volumen de una pirámide aplicable a cualquier tipo de pirámide?

Sí, la fórmula V = (1/3) * B * h es válida para cualquier pirámide, independientemente de la forma de su base.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 6 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Volumen de la Pirámide

Equipo editorial StudySmarter

¿Qué es una pirámide?

Tipos de pirámides