Volumen del Cono: Fórmulas, Ejemplos

Saltar a un capítulo clave

En este artículo comprenderás qué es un cono y los objetos cónicos, cómo determinar su volumen y ejemplos de aplicación de esto.

¿Qué es un cono?

Un cono es un sólido tridimensional que consta de una base circular y una superficie curva continua que se estrecha hasta una punta llamada vértice o ápice.

Algunos ejemplos de objetos con forma cónica son el cono de tráfico, las tapas de los conos de cumpleaños, los conos de helado, las zanahorias, etc.

Volumen de conos Una imagen de conos de tráfico StudySmarter Una imagen de conos de tráfico-StudySmarter Original

Volumen de los cucuruchos Imagen de un cucurucho de helado StudySmarter Una imagen de un cono de helado - StudySmarter Original

Tipos de conos

Hay dos tipos básicos de conos:

Los conos circulares rectos, que tienen su vértice perpendicular o justo encima del centro de su base.

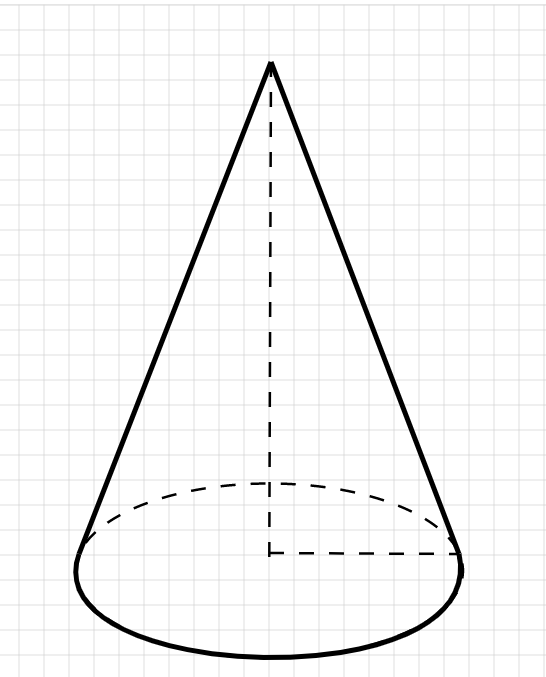
Volumen de un cono Diagrama de un cono StudySmarter

Ilustración de un cono circular recto - StudySmarter Original

Los conoscirculares oblicuos - no tienen su vértice por encima del centro de la base circular y, como tales, no son perpendiculares al centro.

Diagrama del volumen de un cono circular oblicuo StudySmarter Ilustración de un cono circular oblicuo - StudySmarter Original

Derivación del volumen de los conos a partir del volumen de los cilindros

El volumen o capacidad de un cono es un tercio de su cilindro correspondiente. Esto significa que cuando un cono y un cilindro tienen la misma dimensión de base y altura, el volumen del cono es un tercio del volumen del cilindro. Por tanto, se puede obtener un cono dividiendo un cilindro en tres partes. Para visualizarlo, haremos un pequeño experimento.

Experimento sobre la obtención de conos a partir de cilindros

Primero, entendamos lo siguiente: El volumen de un sólido también puede entenderse como su capacidad. La capacidad de un sólido es la cantidad de un líquido -normalmente pensamos en el agua- que puede contener.

Pasemos ahora al experimento. Se puede realizar mediante los siguientes pasos.

Paso 1. Consigue un cilindro regular vacío con una altura y un radio de la base circular conocidos.

Paso 2. Consigue un cono regular vacío con la misma altura y radio que el cilindro.

Paso 3. Llena el cono de agua hasta el borde.

Paso 4. Vierte toda el agua del cono en el cilindro vacío y observa el nivel de agua en el cilindro.

Observa que el cilindro aún no está lleno.

Paso 5. Repite los pasos 3 y 4 por segunda vez en el mismo cilindro que ya tiene agua. Observa que el nivel de agua sube, pero el cilindro aún no se ha llenado hasta el borde.

Paso 6. Repite los pasos 3 y 4 por tercera vez con el mismo cilindro. Observa que ahora el cilindro está lleno hasta el borde.

Este experimento explica que necesitarías 3 conos para hacer un cilindro.

Volumen de conos Una ilustración sobre cómo se relaciona un cono con un cilindro StudySmarter Ilustración de la relación entre un cono y un cilindro - StudySmarter Original

¿Cómo calcular el volumen de un cono?

El volumen de un cono es el espacio tridimensional que ocupa. Es el número de cubos unitarios que caben en él.

Como sabemos que un cono es un tercio de su cilindro correspondiente, es más fácil calcular el volumen de un cono.

Recordemos que el volumen de un cilindro es el producto del área de su base circular por su altura y viene dado por,

$V o l u m e_{C y l i n d e r} = π r^{2} \times h$ .

Por tanto, el volumen de un cono es un tercio del producto del área de su base circular y su altura.

$V o l u m e_{C o n e} = \frac{V o l u m e_{C y l i n d e r}}{3} = \frac{π r^{2} \times h}{3}$

Observa que el volumen de un cono oblicuo se calcula con la misma fórmula que el de un cono regular recto. Esto se debe al principio de Cavalieri, que explica que el volumen de una forma sólida es igual al volumen de su correspondiente objeto oblicuo.

El casquete cónico tiene un radio en la base de 7 cm y una altura de 8 cm. Halla el volumen del cono. Toma $π = 3.14$ .

Solución

Primero escribimos los valores dados $r = 7, h = 8 c m, π = 3.14 .$

El volumen del cono puede calcularse mediante la fórmula,

$V o l u m e_{C o n e} = \frac{π r^{2} \times h}{3} = \frac{3.14 \times 7^{2} \times 8}{3} = \frac{1230.88}{3} = 410.29 c m^{3}$

¿Cómo calcular el volumen de un cono sin altura conocida?

A veces nos pueden pedir que hallemos el volumen de conos sin altura conocida. En este caso, tenemos que buscar una altura oblicua conocida o un ángulo conocido. Con una altura oblicua dada, puedes utilizar el teorema de Pitágoras para calcularla. Por tanto, sea l la altura oblicua,

l^{2} = r^{2} + h^{2} \Rightarrow h = \sqrt{l^{2} - r^{2}}

El teorema de Pitágoras sólo se aplica cuando el radio r y la altura oblicua l están dados, pero no la altura.

Volumen de conos Toda la ilustración sobre el cálculo de un cono con un ángulo subtendido en el vértice StudySmarter Ilustración de un cono con un ángulo subtendido en el vértice - StudySmarter Original

Cuando se da un ángulo, se aplica SOHCAHTOA para obtener el valor de la altura. Si se da el ángulo en el vértice, se utiliza la mitad de ese ángulo para hallar la altura. Así

\tan \frac{θ}{2} = \frac{r}{h} h = \frac{r}{\tan \frac{θ}{2}}

donde;

θ es el ángulo en el vértice,

l es la altura oblicua del cono,

h es la altura del cono

r es el radio de la base del cono.

Volumen del Frustum de un cono

El frustum de un cono o cono truncado tiene la punta (vértice) cortada. Es la forma de la mayoría de los cubos.

Volumen de conos Una ilustración sobre cómo se forma un frustro a partir de un cono StudySmarter Ilustración de cómo se forma un frustum de un cono - StudySmarter Original

Para calcular el volumen de un frustro se utiliza la proporción. Un frustum tiene dos radios: un radio para la superficie circular mayor y otro radio para la superficie circular menor.

Volumen de conos Una imagen que muestra la derivación del volumen de un frustrum StudySmarter Una imagen que muestra la derivación del volumen de un frustro - StudySmarter Original

Sea R el radio de la superficie circular mayor, y r el radio de la superficie circular menor. _Sea hfla altura del frustro, y H la altura del cono cuando esté completo. Y, por último, que hc _seala altura del cono pequeño que se cortó para formar el frustum.

Por tanto, utilizando la proporción tenemos

$\frac{R}{r} = \frac{H}{h_{c}}$

El volumen del frustum es igual a la diferencia entre el volumen del cono grande y el volumen del cono pequeño cortado, y por tanto tenemos

$V o l u m e_{f r u s t u m} = V o l u m e_{b i g c o n e} - V o l u m e_{s m a l l c u t c o n e}$

Pero,

$V o l u m e_{b i g c o n e} = \frac{1}{3} π R^{2} H, V o l u m e_{s m a l l c o n e} = \frac{1}{3} π r^{2} h_{c}$

Por tanto, el volumen del frustro es

$V o l u m e_{f r u s t u m} = \frac{1}{3} π R^{2} H - \frac{1}{3} π r^{2} h_{c}$

Calcula el volumen del siguiente frustro

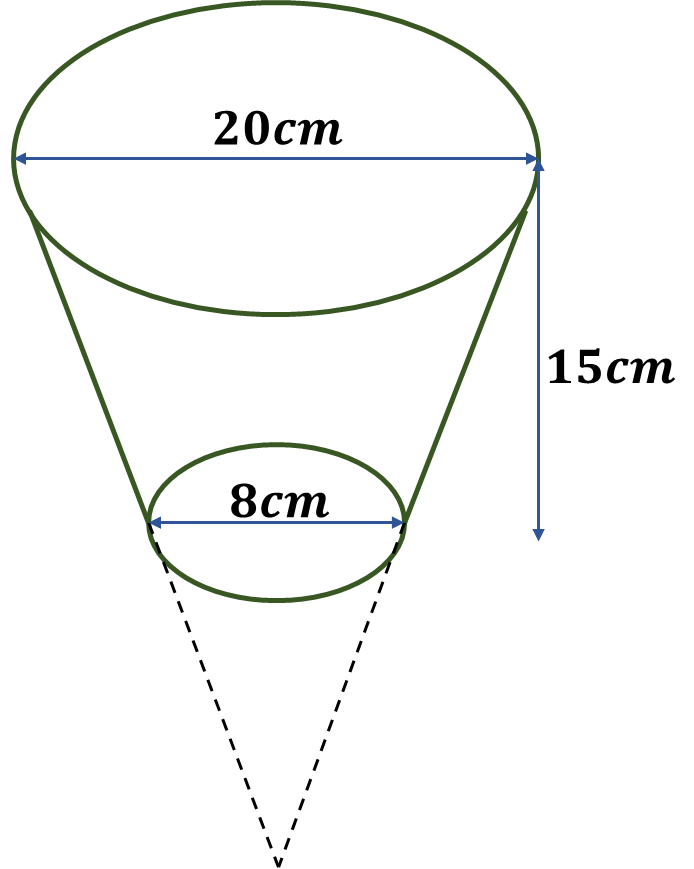
Volumen de un cono Diagrama de un cono StudySmarter

Solución

Escribimos los valores dados,

$R = 20 c m \div 2 = 10 c m r = 8 c m \div 2 = 4 c m h_{f} = 15 c m$

Tenemos que hallar la altura del cono lleno $H$ y la altura del cono pequeño $h_{c}$ ;

$H = h_{f} + h_{c} H = 15 + h_{c}$

utilizando la proporción;

$\frac{R}{r} = \frac{H}{h_{c}}$

Recuerda que

$H = 15 + h_{c} \frac{10}{4} = \frac{15 + h_{c}}{h_{c}} 10 \times h_{c} = 4 (15 + h_{c}) 10 h_{c} = = 60 + 4 h_{c} 10 h_{c} - 4 h_{c} = 606 h_{c} = 60 \frac{6 h_{c}}{6} = \frac{60}{6} h_{c} = 10 c m$

Y así

$H = 15 + h_{c} H = 15 + 10 = 25 c m V o l u m e o f b i g c o n e = \frac{1}{3} π R^{2} H = = \frac{1}{3} \times \frac{22}{7} \times 10^{2} \times 25 = \frac{55000}{21} = 2619.05 c m^{3}$

Utilizando la proporción;

$\frac{R}{r} = \frac{V o l u m e o f b i g c o n e}{V o l u m e o f s m a l l c o n e} \frac{10}{4} = \frac{2619.05}{V o l u m e o f s m a l l c o n e} 10 \times V o l u m e o f s m a l l c o n e = 4 \times 2619.05 V o l u m e o f s m a l l c o n e = \frac{4 \times 2619.05}{10} V o l u m e o f s m a l l c o n e = 1047.62 c m^{3}$

Recuerda que

$V o l u m e o f f r u s t u m = V o l u m e o f b i g c o n e - V o l u m e o f s m a l l c o n e V o l u m e o f f r u s t u m = 2619.05 - 1047.62 V o l u m e o f f r u s t u m = 1571.43 c m^{3}$

Un cilindro tiene un radio $4.2 c m$ y una altura $10 c m$ . Si en el cilindro se colocara un embudo cónico con el mismo radio y altura, halla el volumen del embudo.

Solución

$V o l u m e o f a c y l i n d e r = π r^{2} h V o l u m e o f c y l i n d e r = \frac{22}{7} \times 4.2 \times 4.2 \times 10 V o l u m e o f c y l i n d e r = 554.4 c m^{3}$

Se nos dice que el cono tiene la misma altura y la misma parte superior circular que la del cilindro. Esto significa que el volumen del cono es un tercio del volumen del cilindro.

$V o l u m e o f a c o n e = \frac{1}{3} \times v o l u m e o f a c y l i n d e r V o l u m e o f a c o n e = \frac{1}{3} \times 554.4 V o l u m e o f a c o n e = 184.8 c m^{3}$

Volumen del cono - Puntos clave

Un cono es un sólido tridimensional que consta de una base circular y una superficie curva continua que se estrecha hasta una punta llamada vértice.
El cono circular recto y los conos circulares oblicuos son los dos tipos de conos.
Un cono es un tercio de un cilindro.
El volumen de un cono es un tercio del área de la base circular multiplicado por su altura.
El frústum de un cono o un cono truncado tiene la punta (vértice) cortada.

Tarjetas en Volumen del Cono 1

Empieza a aprender

3 conos forman un cilindro.

Verdadero

Aprende con 1 tarjetas de Volumen del Cono en la aplicación StudySmarter gratis

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Volumen del Cono

¿Cómo se calcula el volumen de un cono?

El volumen de un cono se calcula con la fórmula V = (1/3)πr²h, donde r es el radio de la base y h es la altura.

¿Qué es el volumen de un cono?

El volumen de un cono es el espacio que ocupa en tres dimensiones y se mide en unidades cúbicas.

¿Cuál es la fórmula para el volumen de un cono?

La fórmula para el volumen de un cono es V = (1/3)πr²h.

¿Cuál es la unidad de medida para el volumen de un cono?

La unidad de medida para el volumen de un cono es la unidad cúbica, como centímetros cúbicos (cm³) o metros cúbicos (m³).

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 8 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Volumen del Cono

Equipo editorial StudySmarter