Las poleas son lo que llamamos máquinas simples. Sin utilizar un motor, pueden ayudar a multiplicar la cantidad de fuerza aplicada para levantar un objeto. Cuando juntas dos o más ruedas y las rodeas con una cuerda, has creado una gran máquina elevadora. La carga es la cantidad de masa del objeto que hay que mover, y el esfuerzo es la fuerza necesaria para mover el objeto.
A medida que aumentes el número de poleas de un sistema, necesitarás más cuerda para arrastrar la carga a lo largo de una distancia. Por tanto, tendrás que aplicar la fuerza durante más tiempo cuando tengas más poleas.
Cómo funcionan las poleas
A medida que añades más poleas, aumentas la ventaja mecánica y resulta muy fácil levantar la misma carga. Sin embargo, antes de continuar, definamos qué es la ventaja mecánica y tengamos claras las diferencias entre peso y masa.
El peso es la cantidad de fuerza con la que la gravedad tira de un objeto hacia el suelo. Se mide en newtons (N).
La masa es la medida de la cantidad de sustancia contenida en un objeto, que se mide en kilogramos (kg).
La ventaja mecánica es la relación entre la fuerza que realiza el trabajo útil y la fuerza aplicada. Es la medida de cómo las máquinas simples multiplican las fuerzas.
Si tuvieras un saco con una masa de unos 40 kg, puedes calcular el peso de la siguiente forma \(peso = masa \cdot gravedad).
\(Peso = 40 kg \cdot 9,8 m/s^2 = 392 kg \cdot m /s^2 = 392 N\).
La gravedad terrestre en newtons es aproximadamente diez veces la masa en kilogramos.
Sistema de poleas de una rueda
Una simple polea te ayuda a elevar cargas invirtiendo la dirección de la carga. Si tiras de la cuerda hacia abajo, la carga sube, como se muestra en el diagrama siguiente.
Polea de una rueda. Imagen:César Rincón CC BY-SA 3.0,
Sistema de poleas de dos ruedas
Añadiendo una rueda más al sistema, ahora puedes reducir el esfuerzo que emplearías para levantar la misma carga utilizando un sistema de poleas de una sola rueda. Si tuviera mi saco con una masa de 40 kg y un peso de 400 N, esta vez el peso de la carga se repartirá entre las dos poleas. Por tanto, necesitarás la mitad del esfuerzo necesario para tirar de la carga. Las poleas con más ruedas proporcionan más ventaja mecánica.
Con el sistema de dos ruedas, cuando tiras de 5 metros de cuerda, mueves la carga sólo la mitad de la distancia. Es decir, 2,5 metros.
Sistema de poleas de dos ruedas. Imagen: dominio público.
Sistema de poleas de cuatro ruedas
Si unimos cuatro ruedas con una cuerda para formar una polea, observaremos que cuatro tramos del peso quedarán colgados sobre las ruedas de la polea. Eso significará que el peso de nuestro saco de 400 N (40 kg) se repartirá ahora entre cada rueda, y sólo necesitaremos una cuarta parte de la fuerza para mover la carga que con la polea simple de una rueda.
La ventaja mecánica de este sistema de poleas será el doble que en el de dos ruedas. Sin embargo, para elevar la carga una distancia de 5 metros, habrá que tirar de la cuerda cuatro veces esa distancia. Es decir, 20 metros.
Sistema de poleas de cuatro ruedas. Imagen: dominio público.
Tipos de poleas
Entre las máquinas simples hay tres tipos de sistemas de poleas:
Poleas fijas: también se denominan de punto único. Este tipo de polea permanece fija mientras la carga permanece en un lado de la rueda y el esfuerzo se aplica en el otro lado. Por ello, necesitarás la misma cantidad de fuerza para levantar el objeto.
Poleas móviles: se diferencian de las poleas fijas en que el sistema de poleas se mueve realmente con la carga. A diferencia de la polea fija, ésta no cambia la dirección, sino que multiplica la fuerza que se ejerce sobre la carga. Es útil para cargas más pesadas, y no necesitarás tanto esfuerzo para levantar la carga.
Hallar la aceleración de una carga
Aquí tienes algunos ejemplos prácticos para hallar la aceleración de una carga. Para algunos de ellos utilizamos ecuaciones SUVAT.
Hallar la aceleración
Si estas dos partículas del diagrama siguiente se liberan del reposo, ¿cuál será la aceleración?
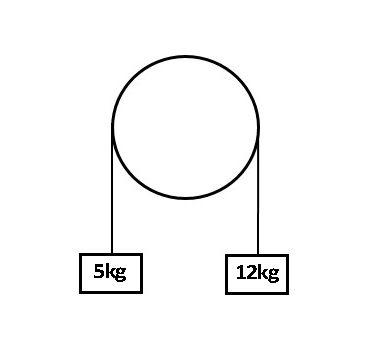
Respuesta:
La partícula de mayor masa descenderá, y la de menor masa ascenderá. Tomemos la partícula de 5 kg de masa como partícula a, y la de 12 kg como partícula b.
Para aclarar el peso de cada partícula tenemos que multiplicar su masa por la gravedad. Por tanto, utilizamos g = 9,8 m / s².
Peso de a = 5g
Peso de b = 12g
Ahora puedes modelar una ecuación para la aceleración y la tensión de cada partícula.
\(T - 5kg \cdot g = 5kg \cdot \text{ a [Partícula a] [Ecuación 1]}\)
\(12kg \cdot g - T = 12kg \cdot \text{ a [Partícula b] [Ecuación 2]}\})
Ahora resuelve esto simultáneamente. Suma ambas ecuaciones para eliminar la variable T.
\(7kg \cdot g = 17kg \cdot a\)
Si tomas g = 9,8 m / s².
\(a = 4,0 m/s^2)
Investigando dos posibilidades
Dos partículas de masa 8 kg y m kg están unidas por una cuerda tensa que pasa sobre una clavija lisa. Ambas partículas cuelgan verticalmente con una de ellas en reposo. La partícula se suelta. Dado que la aceleración es de 5 m/s², halla la masa m.
Contesta:
Dibujemos un diagrama que se ajuste a la pregunta.
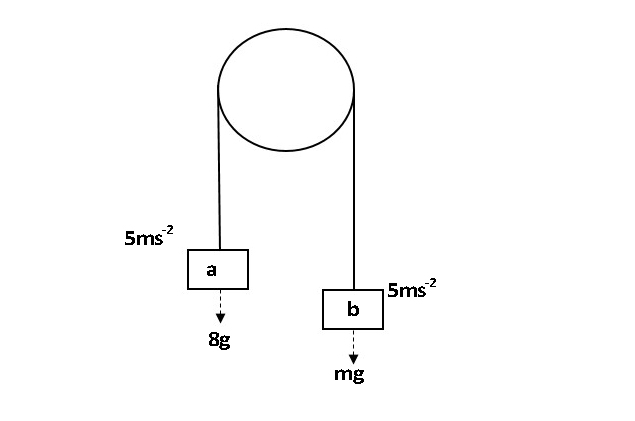
Tomemos la partícula con la masa de 8 kg como partícula a, y la partícula con masa desconocida como b.
Para que todo esto funcione, la masa de la partícula b debe ser mayor o menor que la de la partícula a. Esto determinará qué partícula acelerará. Así que tendremos que investigar ambas posibilidades.
Así que veamos la situación en la que m > 8.
Resolviendo la partícula a verticalmente
\(T - 8 kg \cdot g = 8 kg \cdot 5 m/s^2 \qquad T = 40 N + 8 kg \cdot (9,8 m/s^2) \qquad T = 118,4N\)
Resolviendo la partícula b verticalmente
\(mg - 118,4 N = 5 m/s^2 \cdot m \space mg -5m/s^2 \cdot m = 118,4N \space m(g-5m/s^2) = 118,4N\)\(m = \frac{118,4 N}{g - 5 m/s^2} = 24,7 kg\)
Esa sería la masa de la partícula b en un caso en el que m > 8.
Tomemos ahora la situación en la que m < 8
\(8 kg \cdot g - D = 8 kg \cdot 5 m/s^2\)
T = 38,4N
Resolviendo la partícula b verticalmente
\(38,4 N - mg = 5 m/s^2 \cdot m \qquad 38,4 N = 5 m/s^2 \cdot m + mg \qquad 38,4 N = m (5m/s^2 + g)\)\(m = \frac{38,4N}{5 m/s^2 + g}\)
m = 2,6 kg
Ahora tenemos una masa para ambos escenarios. Si la masa de la partícula a> b, b acelerará hacia arriba mientras a acelera hacia abajo. En cambio, si a < b, a acelerará hacia arriba mientras b acelera hacia abajo.
SUVAT
El diagrama muestra dos partículas que están unidas por una cuerda ligera inextensible. La partícula a, de 5 kg, está sobre una superficie horizontal rugosa y la partícula b, de 3 kg, cuelga del otro extremo de la cuerda. La cuerda pasa por encima de una polea ligera lisa. La velocidad inicial de ambas partículas es de 2 ms-1 y una fuerza de rozamiento constante de 4N actúa contra a. Las partículas disminuyen su velocidad y se detienen antes de que a llegue a la polea o b caiga. Halla
La aceleración de las partículas.
La distancia que recorren las partículas antes de detenerse.
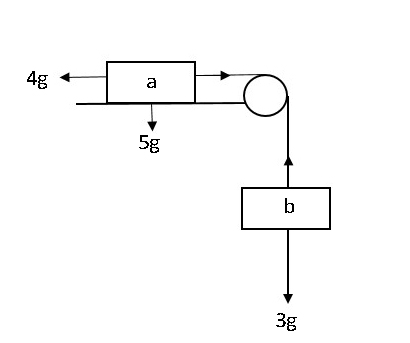
Figura 7. Ejemplo de polea en SUVAT
Responde:
- \(T -4g = 5a \text{ [Ecuación 1] [Partícula a resuelta horizontalmente]}\})
\(3g - T = 3a \text{ [Ecuación 2] [Partícula b resuelta verticalmente]}\})
Sumando las ecuaciones
\(-g = 8a)
\(a = \frac{-g}{8}\)
Toma g como 9,8 ms-2
\(a = -1,225 ms^{-2}\)
s = x
u = 2 ms-1
v = 0
a = -1,225 ms-2
t =?
Utilizaremos la ecuación que no tiene t, ya que no disponemos de información al respecto.
\(v^2 = u^2 + 2as\)
\(0 = 4ms^{-1} - 2 \cdot 1,225 ms^{-2}\)
\(s = \frac{4ms^{-1}} {2 \cdot 1,225 ms^{-2}})
\(s = 1,6 m\)
Poleas - Puntos clave
- Una polea es un conjunto de ruedas sobre las que se enrosca una cuerda para facilitar la elevación de objetos.
- Hay tres tipos de sistemas de poleas. Poleas fijas, móviles y compuestas.
- Cuantas más ruedas tengas en tu sistema, más ventaja mecánica tendrás para levantar la carga.
- Al incluir una rueda en tu sistema de poleas de una rueda, reduces la cantidad de fuerza necesaria para levantar la carga, pero tendrás que mover tu cuerda el doble de distancia para que la carga recorra la distancia que habría recorrido si fuera un sistema de una rueda.
- Las ecuaciones SUVAT pueden utilizarse para resolver ciertos problemas de poleas.
Imágenes
Polea de una rueda https://commons.wikimedia.org/w/index.php?curid=643667
Aprende con 15 tarjetas de Poleas en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Poleas
Pon a prueba tus conocimientos con tarjetas de opción múltiple
TU PUNTUACIÓN
Tu puntuación
¡Únete a la aplicación StudySmarter y aprende de manera eficiente con millones de tarjetas y mucho más!
Aprende con 15 tarjetas de Poleas en la aplicación StudySmarter gratis
¿Ya tienes una cuenta? Iniciar sesión
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
