Analizando Gráficas de Polinomios: Funciones, Ejemplos

Saltar a un capítulo clave

Comportamiento final de las funciones polinómicas

Dada una función polinómica, el comportamiento final es lo que le ocurre a la gráfica a medida que x se acerca a los límites del dominio. Si dibujamos la gráfica de una función polinómica, el comportamiento final es lo que le ocurre a la gráfica a medida que nos acercamos a los "extremos" del eje real.

Ejemplo que muestra el comportamiento final de los polinomios, Jordan Madge- StudySmarter Originals

Arriba está la gráfica de $f (x) = x^{2} - 3 x - 4$ . Aquí podemos ver que a medida que x se hace más y más grande, la gráfica aumenta. Decimos que a medida que x tiende a infinito, la función tiende a infinito. Del mismo modo, decimos que a medida que x se acerca al infinito negativo, la función se acerca al infinito positivo, ya que a medida que x se hace cada vez más pequeña, la gráfica también sube.

Comportamiento final de las funciones polinómicas, Gráfica que muestra el comportamiento final, Geogebra Gráfico que muestra el comportamiento final del polinomio cúbico, Jordan Madge- StudySmarter Originals

Arriba está la gráfica de $f (x) = x^{3} - 3 x - 2$ . Aquí podemos ver que a medida que x se acerca al infinito positivo, la función se acerca al infinito positivo, sin embargo, a medida que x se acerca al infinito negativo, la gráfica se acerca al infinito negativo.

Una versión abreviada de escribir "x tiende a infinito" es $x \to \infty$ . Así, en el ejemplo anterior, podríamos escribir: como $x \to \infty$ , $f (x) \to \infty$ y como $x \to - \infty$ , $f (x) \to - \infty$

¿Qué determina el comportamiento final de una función polinómica?

El grado de un polinomio es la mayor potencia que tiene un polinomio. Por ejemplo, la función polinómica es un polinomio de grado 5. El coeficiente principal de una función polinómica es el término de mayor grado del polinomio. Así, para el polinomio, el coeficiente principal es 7 y el grado es 5.

Cuando x se hace muy grande o muy pequeña (como $x \to \infty$ o $x \to - \infty$ ), el coeficiente principal se vuelve significativo porque ese término tomará el control y crecerá mucho más rápido que los demás términos. Por tanto, para determinar el comportamiento final de un polinomio, sólo tenemos que fijarnos en el grado y el coeficiente principal para sacar una conclusión. Hay cuatro escenarios posibles.

Caso	Grado	Coeficiente Líder	Comportamiento final	Ejemplo
1	Incluso	Positivo	Como 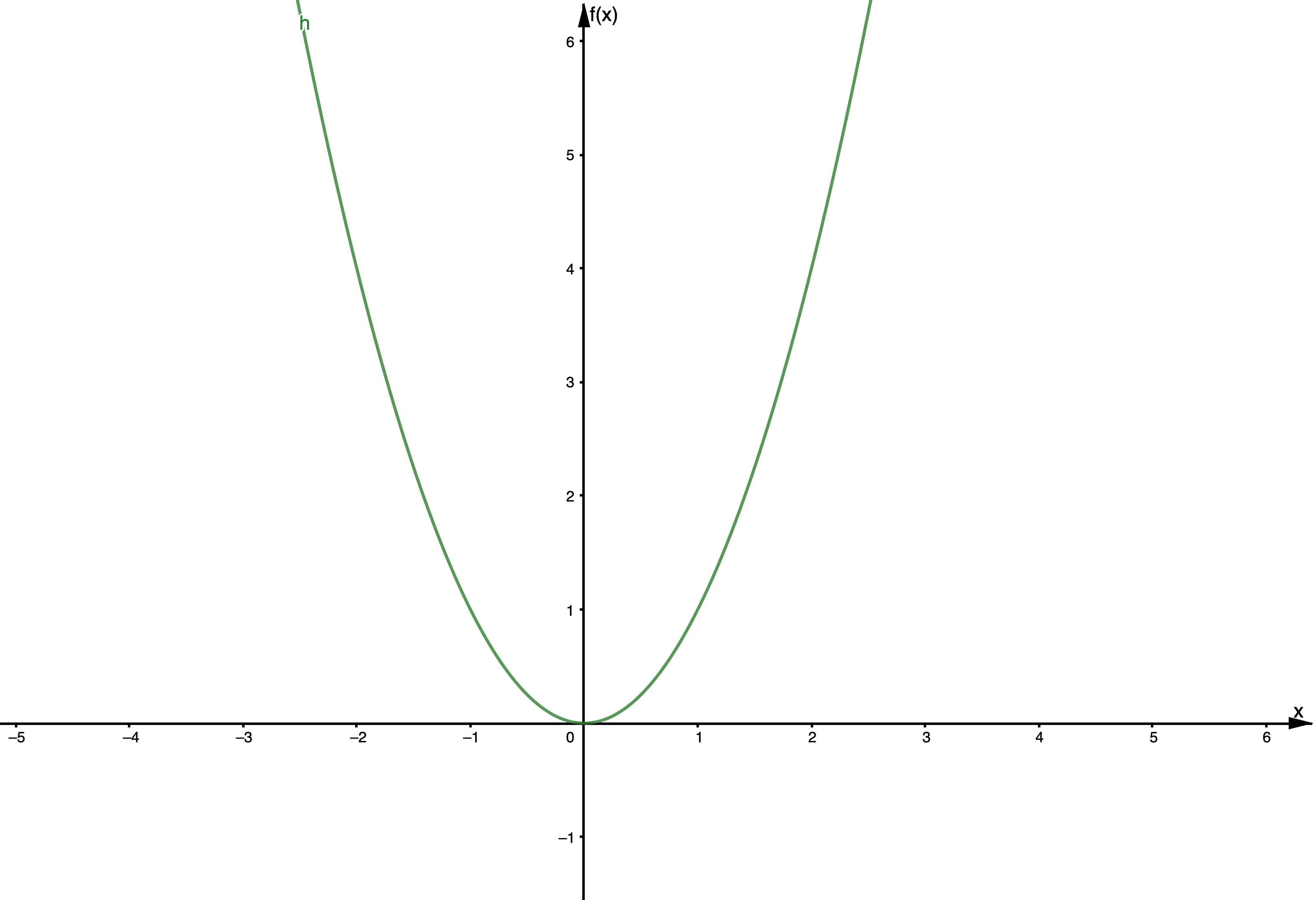$x \to \infty$ , $f (x) \to \infty$ Como $x \to - \infty$ , $f (x) \to \infty$
2	Par	Negativo	Como 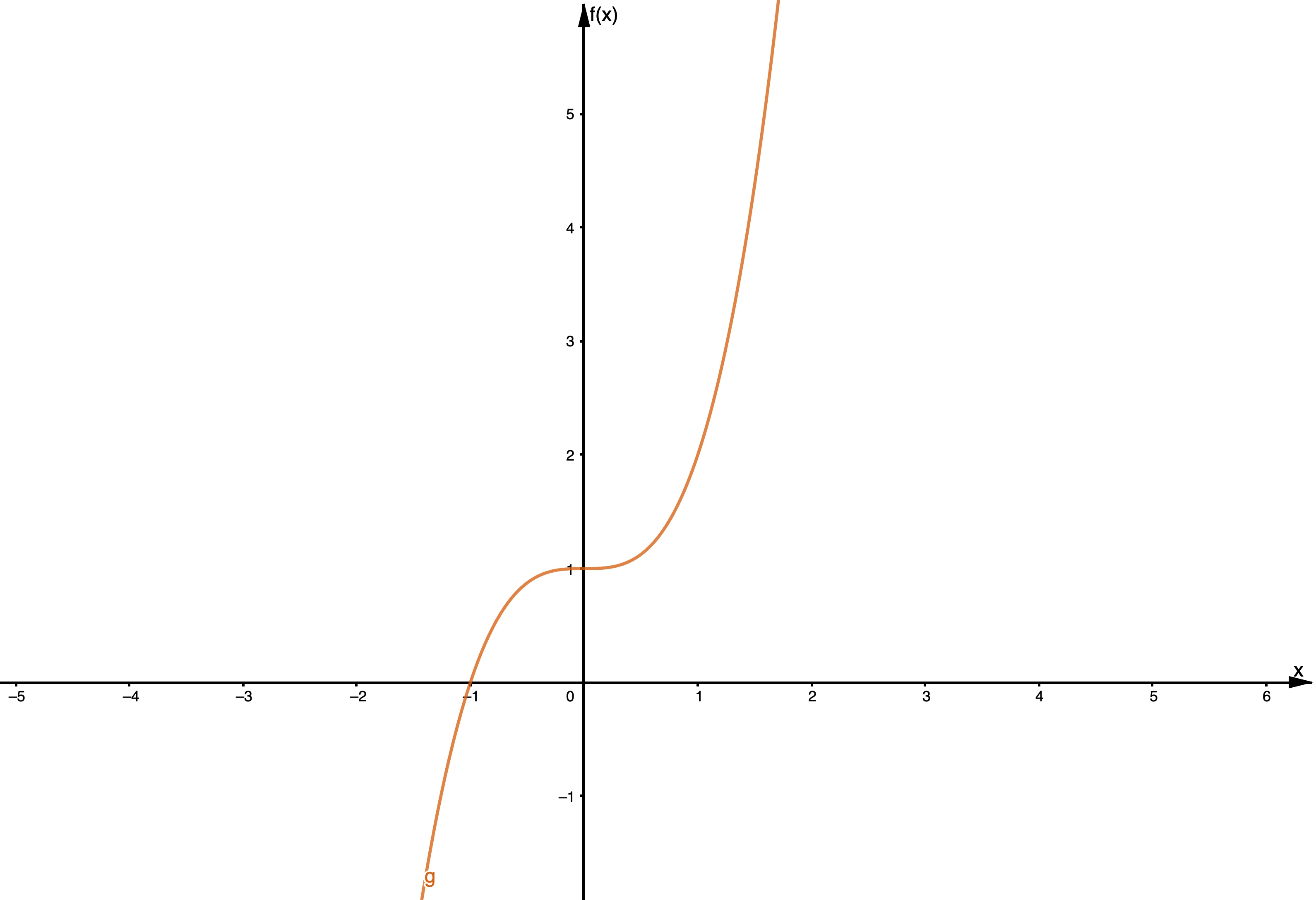$x \to \infty$ , $f (x) \to - \infty$ Como $x \to - \infty$ , $f (x) \to - \infty$	Comportamiento Final de la Función Par, Jordan Madge- StudySmarter Originals.
3	Impar	Positivo	Como 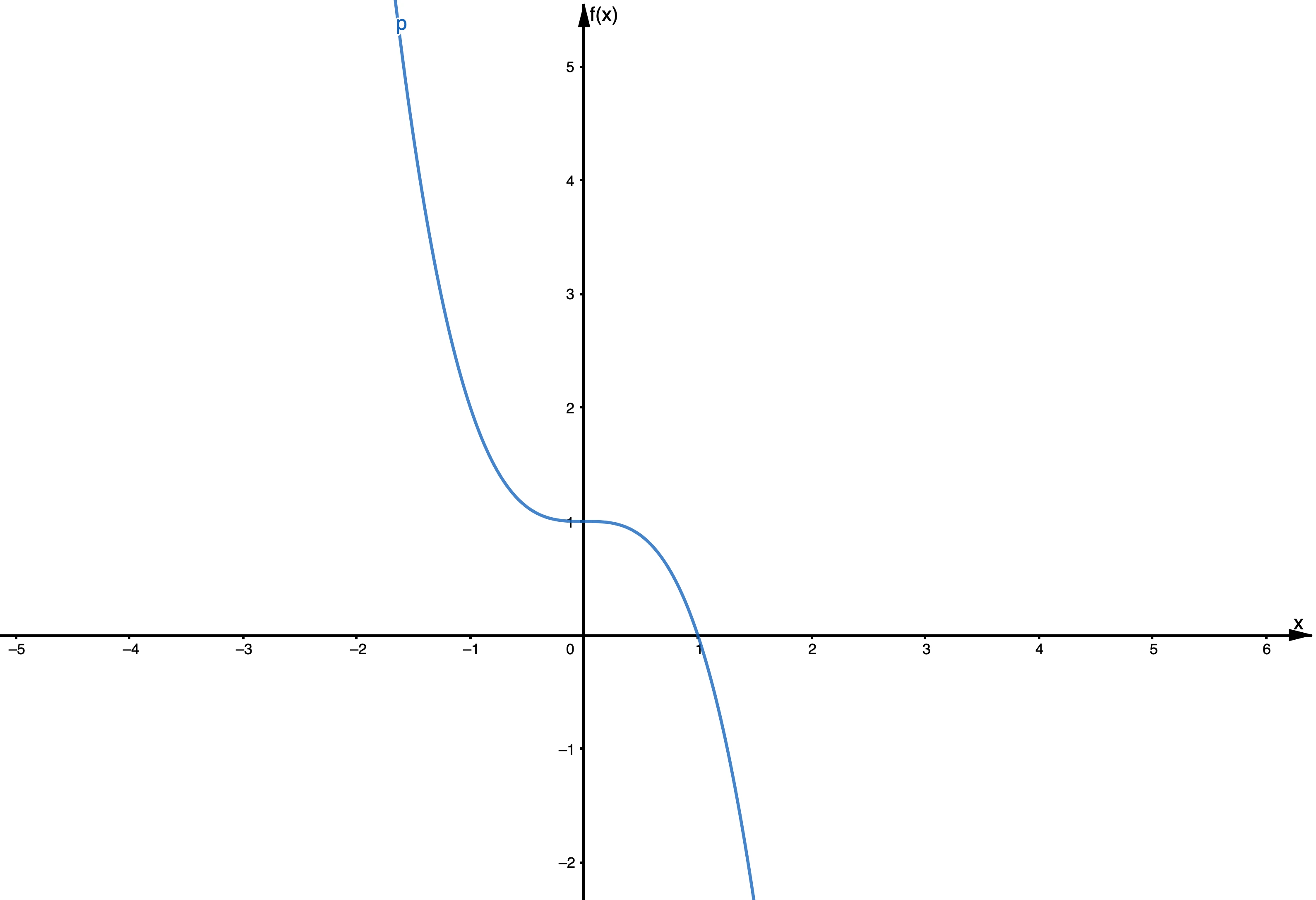$x \to \infty$ , $f (x) \to \infty$ As $x \to - \infty$ , $f (x) \to - \infty$	Comportamiento Final de la Función Impar, Jordan Madge- StudySmarter Originals.
4	Impar	Negativo	Como 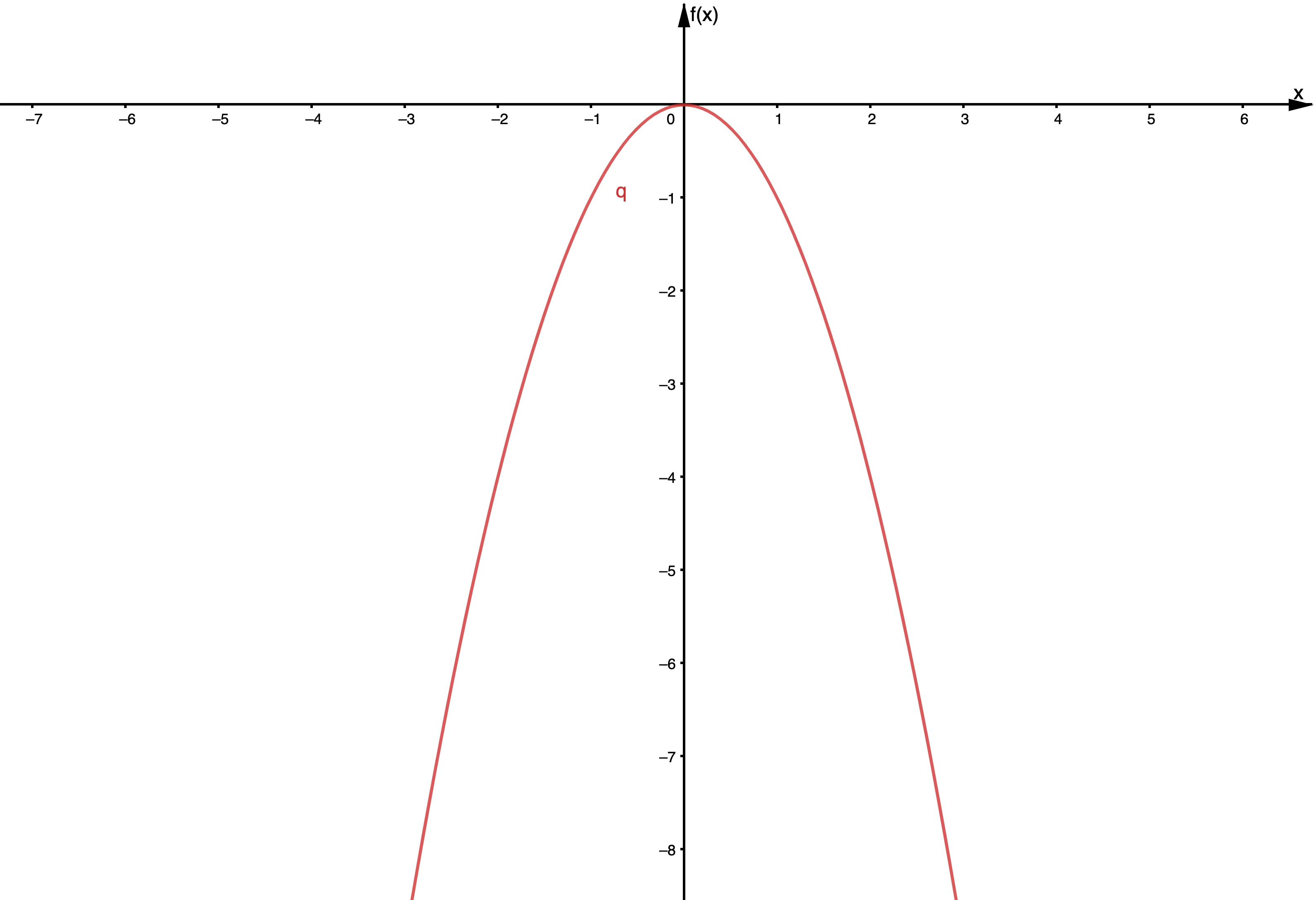$x \to \infty$ , $f (x) \to - \infty$ As $x \to - \infty$ , $f (x) \to \infty$	Comportamiento Final de la Función Impar, Jordan Madge- StudySmarter Originals.

$f (x) = x^{2} + 3 x + 2$ Determina el comportamiento final de la función polinómica .

Solución:

Aquí, el grado es 2, que es par, y el coeficiente principal es 1, que es positivo. Por tanto, tenemos el caso 1 y como $x \to \infty$ $f (x) \to \infty$ y como $x \to - \infty$ , $f (x) \to \infty$ .

$f (x) = - x^{4} + 3 x^{3} + x - 2$ Determina el comportamiento final del polinomio.

Solución:

Aquí, el grado es 4, que es par, y el coeficiente principal es -1, que es negativo.

Por lo tanto, tenemos el caso 2 y así $x \to \infty$ , $f (x) \to - \infty$ y como $x \to - \infty$ , $f (x) \to - \infty$ .

$f (x) = 2 x^{3} + 7 x^{2}$ Determina el comportamiento final del polinomio .

Solución:

Aquí, el grado es 3, que es impar, y el coeficiente principal es 2, que es positivo. Por tanto, tenemos el caso 3 y por tanto como $x \to \infty$ , $f (x) \to \infty$ y como $x \to - \infty$ , $f (x) \to - \infty$ .

Determina el comportamiento final del polinomio $f (x) = - 7 x^{5} + 3 x^{2} - 1$

Solución:

Aquí, el grado es 5, que es impar, y el coeficiente principal es -7, que es negativo. Por tanto, tenemos el caso 4 y por tanto como $x \to \infty$ , $f (x) \to - \infty$ y como $x \to - \infty$ , $f (x) \to \infty$ .

Ceros de las funciones polinómicas

Los ceros de un polinomio son los valores de x que hacen que el polinomio sea igual a cero. A menudo, denotamos una función polinómica utilizando la notación p(x). Por tanto, los ceros pueden hallarse igualando p(x) a cero y resolviendo para x. Los ceros son también las intersecciones x de la función.

Halla los ceros de la función polinómica $p (x) = (x - 1) (x - 2) (x - 3)$

Solución:

Igualando p(x) a cero, obtenemos $(x - 1) (x - 2) (x - 3) = 0$ .

Resolviendo para x, obtenemos $x = 1, x = 2, x = 3$ .

Encuentra los ceros de la función polinómica $p (x) = (x + 2) (x + 1)$ .

Solución:

Igualando p(x) a cero, obtenemos $(x + 2) (x + 1) = 0$ .

Por tanto, $x = - 2, - 1$

Localización de ceros

Supongamos que tenemos la función polinómica $p (x) = - x^{2} + 2 x + 1$ . Si calculamos $p (2)$ obtenemos $p (2) = {- (2)}^{2} + 2 (2) + 1 = 1$ que es positivo. Si calculamos $p (3)$ obtenemos $p (3) = - {(3)}^{2} + 2 (3) + 1 = - 2$ que es negativo.

El principio de localización establece que para la función polinómica $p (x)$ si $p (a) < 0$ y $p (b) > 0$ entonces debe haber un cero entre a y b.

Localización de Ceros, Ejemplo, Geogebra Localizar Ceros Ejemplo, Jordan Madge- StudySmarter Originals

Arriba está el gráfico de $f (x) = x^{2} + 3 x + 2$ . Si nos fijamos en $f (- 1.5),$ vemos que es negativa. Si miramos f(0), vemos que es positiva. Es evidente que debe haber un cero entre $x = - 1.5$ y $x = 0$ porque la gráfica debe cruzar el eje x en algún punto para pasar de ser negativa a positiva. Ésta es la teoría en la que se basa el principio de localización. Es realmente útil para gráficas en las que puede ser más difícil localizar los ceros utilizando métodos convencionales de resolución, como los cuárticos (polinomios de orden 4), los quínticos (polinomios de orden 5) o los polinomios de orden superior.

Utiliza el principio de localización para demostrar que para la función $p (x) = x^{3} + 3 x + 1$ , existe una raíz entre $x = - 1$ y $x = 0 .$

Solución:

$p (- 1) = - 1 - 3 + 1 = - 3,$

$p (0) = 0 + 0 + 1 = 1$

Gráfica de funciones polinómicas

En este apartado, reuniremos parte de lo que ya hemos tratado para representar gráficamente funciones polinómicas. Para representar gráficamente cualquier función polinómica, hay cuatro pasos principales:

Paso 1: Determina los ceros que pueda tener la gráfica.

Paso 2: Elabora una tabla de valores.

Paso 3: Determina el comportamiento final de la función polinómica.

Paso 4 : Utiliza la información anterior para dibujar la gráfica.

$f (x) = x^{3} - 1$ Dibuja la gráfica de la función polinómica .

Solución:

Paso 1: Determina los posibles ceros.

$x^{3} - 1 = 0$ Igualando la función a cero, obtenemos . Podemos factorizarla para obtener $(x - 1) (x^{2} + x + 1) = 0$ y, por tanto, obtenemos $x = 1$ como único cero real.

Paso 2: Elabora una tabla de valores.

x	-1	0	1	2	3
f(x)	-2	-1	0	7	26

Arriba he elegido algunos valores de x y he calculado los valores correspondientes de f(x).

Paso 3: Determina el comportamiento final de la función polinómica.

Este polinomio es de grado impar y el polinomio principal es 1, que es positivo. Por tanto, tenemos como $x \to \infty$ , $f (x) \to \infty$ y como $x \to - \infty$ , $f (x) \to - \infty$ .

Paso 4: Utiliza la información anterior para dibujar la gráfica.

Graficar polinomios, ejemplo, Geogebra

Ejemplo de graficación de polinomios, Jordan Madge- StudySmarter Originals

Funciones pares e impares

Una vez que hemos dibujado la gráfica de nuestra función polinómica, podemos querer determinar si se trata de una función par o impar. Una función par se da cuando tenemos simetría respecto al eje y. En otras palabras, una función es par cuando $f (x) = f (- x)$ para todos los valores de x. Una función impar se da cuando $- f (x) = f (- x)$ .

Funciones pares e impares, Ejemplo, Geogebra Ejemplo de funciones pares e impares, Jordan Madge- StudySmarter Originals

Arriba está la gráfica de $y = x^{4} - 3$ . Podemos ver que es una función par porque hay simetría respecto al eje y. Siempre que tenemos simetría respecto al eje y, tenemos que $f (x) = f (- x)$ .

Funciones pares e impares, Ejemplo, Geogebra

Ejemplo de Funciones Pares e Impares, Jordan Madge- StudySmarter Originals

Arriba está la gráfica de $y = \frac{1}{2} x^{5}$ . Podemos ver que es una función impar porque $- f (x) = f (x)$ para todos los valores de x.

Puntos de inflexión de las funciones polinómicas

Un punto de inflexión en un gráfico es un punto en el que el gráfico pasa de aumentar a disminuir. En otras palabras, la gráfica pasará de ir "hacia arriba" a ir "hacia abajo" o viceversa. Los máximos locales son específicamente cuando el gráfico pasa de creciente a decreciente. Los mínimos locales son, concretamente, cuando el gráfico pasa de decreciente a creciente.

El plural de máximo es máximos y el plural de mínimo es mínimos. El término que engloba las dos palabras es extremos.

Puntos de inflexión, Ejemplo, Geogebra

Ejemplo de puntos de inflexión, Jordan Madge- StudySmarter Originals

En el gráfico anterior, podemos ver un punto de inflexión que se produce en $(0, 0) .$ En este punto, la gráfica pasa de creciente a decreciente, por lo que se trata de un máximo local.

Análisis de gráficas de polinomios - Puntos clave

El comportamiento final de una función polinómica es lo que le ocurre a la gráfica cuando x se aproxima al infinito positivo o negativo.
Podemos determinar el comportamiento final de cualquier polinomio observando el coeficiente principal y el grado del polinomio.
El cero de una función polinómica es el punto en el que cruza el eje x. Se puede determinar igualando la función polinómica a cero y resolviendo para x.
Podemos utilizar el principio de localización para determinar los valores entre los que se encuentran los ceros.
Las funciones pares son funciones que tienen simetría respecto al eje x y $f (x) = f (- x)$
Las funciones impares son funciones en las que $f (- x) = - f (x)$
Un punto de inflexión es un punto en el que una función pasa de creciente a decreciente o viceversa.
Un mínimo local se produce cuando una función pasa de decreciente a creciente.
Un máximo local se produce cuando una función pasa de creciente a decreciente.

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Analizando Gráficas de Polinomios

¿Qué es un polinomio?

Un polinomio es una expresión algebraica compuesta de variables y coeficientes, combinados usando sumas, restas y multiplicaciones.

¿Cómo identificar las raíces de un polinomio en una gráfica?

Las raíces de un polinomio en una gráfica son los puntos donde la curva cruza el eje x, es decir, donde y = 0.

¿Qué represente el grado de un polinomio?

El grado de un polinomio indica el exponente más alto de su variable; determina el número de posibles raíces y la forma básica de la gráfica.

¿Cómo afecta el coeficiente principal la gráfica de un polinomio?

El coeficiente principal afecta la amplitud y orientación de la gráfica: si es positivo, la gráfica se abre hacia arriba; si es negativo, se abre hacia abajo.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 11 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Analizando Gráficas de Polinomios

Equipo editorial StudySmarter

Comportamiento final de las funciones polinómicas

¿Qué determina el comportamiento final de una función polinómica?