Ecuaciones de aproximación de ángulos pequeños
Hay tres ecuaciones que podemos utilizar para la aproximación de ángulos pequeños: una para \(\sin \theta\), otra para \(\cos \theta\) y otra para \(\tan \theta\).
\(\sin \theta \aprox \theta\)
\(el coseno de la teta, aproximado a 1 - fracción de la teta 2)
\(Tan \theta \aprox \theta)
Aproximación de ángulo pequeño para sen
La suposición de que \(\sin \theta \approx \theta\) puede entenderse mejor si observamos las gráficas de y = x e y = sen x.
 Gráfica de las rectas y=x (roja) e y=sin x (azul)
Gráfica de las rectas y=x (roja) e y=sin x (azul)
Ahora, como puedes ver alrededor de x = 0, las gráficas de y = x e y = sinx están muy próximas entre sí.
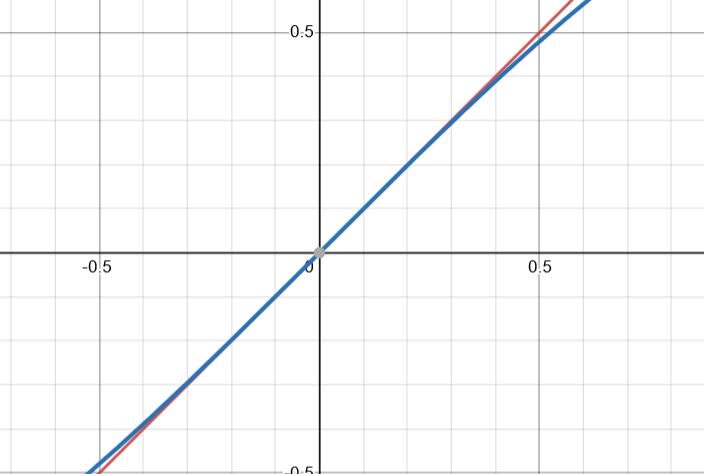
Gráfica de las rectas y=x (roja) e y=sin x (azul) alrededor de x=0
Por eso, para ángulos muy pequeños, podemos decir que \(\sin \theta \aprox \theta\).
Aproximación de ángulo pequeño para cos
La aproximación del coseno no es tan sencilla como la del seno. La aproximación del ángulo pequeño para el cos se obtiene utilizando el resultado de la aproximación del ángulo pequeño que obtuvimos para el sen, y una fórmula de ángulo doble. Utilizamos la fórmula del ángulo doble:
\(\cos 2x = 1 - 2 \sin^2 x\)
Ahora bien, si decimos que \(\cos 2x = \cos \theta\) entonces \(x = \frac{\theta}{2}\). Por tanto, \(\cos \theta = 1- 2 \sin^2\Big( \frac{\theta}{2} \Big)\)
Sabemos por nuestro cálculo anterior que para un valor pequeño de \(\theta\) suponemos que
\(\cos \theta = 1 - 2 \Big(\frac{\theta}{2} \Big)^2\)
Lo que, simplificado, nos da la aproximación de ángulo pequeño para cos:
\(\cos \theta \aprox 1 - \frac{\theta^2}{2}\)
Aproximación de ángulo pequeño para tan
Para la aproximación de ángulos pequeños de tan, utilizamos la misma lógica que para sen. Observando las gráficas de y = tanx e y = x,
 Gráfica de las rectas y=x (roja) e y=tan x (azul)
Gráfica de las rectas y=x (roja) e y=tan x (azul)
De nuevo, para valores próximos a x = 0, vemos que las dos funciones están muy próximas entre sí:
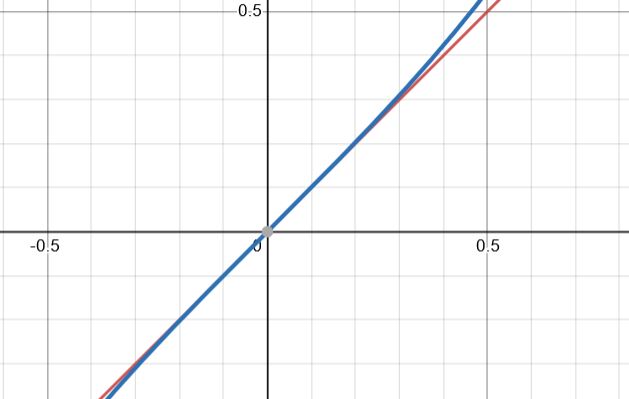
Gráfica de las rectas y=x (roja) e y=tan x (azul) en torno a x=0
Por tanto, suponemos que para valores pequeños de \(\theta, \espacio \tan \theta \aprox \theta\)
Cómo resolver preguntas utilizando la aproximación del ángulo pequeño
Las fórmulas derivadas anteriormente pueden utilizarse en preguntas y problemas para facilitar y agilizar su resolución. Veremos algunos ejemplos de cómo aplicarlas.
Cuando \(\theta\) es pequeño, demuestra que \(\frac{\cos \theta}{\sin \theta}\) puede aproximarse por \(\frac{2 - \theta^2}{2 \theta}\).
Para resolver esta cuestión, tendremos que utilizar las aproximaciones de ángulo pequeño para sen y cos: \(\sin \theta \approx \theta, \cos \theta \approx 1 -\frac{\theta^2}{2}\). Ahora podemos sustituir esto por \frac(\frac{cos \theta}{\sin \theta}\), lo que nos da \frac(\frac{1-\frac{\theta^2}{2}{\theta}\). Podemos simplificar esta expresión multiplicando arriba y abajo por 2: \frac(\frac{2-\frac{2\theta^2}{2}{2}{2\theta}\), que se simplifica a \frac(\frac{2-\theta^2}{2\theta}\), como exige la pregunta.
a) Cuando x es pequeño, demuestra que tan (3x) cos (2x) puede aproximarse por \(3x - 6x^3\)
b) Por tanto, aproxima el valor de tan (0,3) cos (0,2) a 3 sf
Esta pregunta debe responderse en dos partes: a y b. Empecemos por ver cómo resolveríamos a). Necesitaremos utilizar los hechos tan x≈ x y \(\cos x \approx 1 - \frac{x^2}{2}\). Sustituyendo esto en tan (3x) cos (2x), obtenemos \(3x \Big(1-\frac{(2x)^2}{2} \Big)\)o \(3x(1-2x^2)\). Multiplicando el paréntesis por 3x: \(3x-6x^3\) como es debido.
Para la parte b, tenemos que hallar el valor de tan para 0,3 y de cos para 0,2. Conocemos las expresiones para tan 3x y cos 2x, por tanto 3x = 0,3 y 2x = 0,2 nos da x = 0,1. Ahora podemos introducir 0,1 en la expresión que hemos encontrado antes: \(3 (0.1) - 6(0.1)^3 = 0.294\)
Si el ángulo se da en grados, tendrás que convertirlo primero a radianes para utilizar la aproximación del ángulo pequeño. Puedes utilizar la fórmula \(radián = grado \cdot \frac{\pi}{180}\)
Aproximación del ángulo pequeño - Puntos clave
La aproximación del ángulo pequeño puede utilizarse para facilitar el trabajo con funciones trigonométricas cuando se consideran ángulos cercanos a 0 rad.
La aproximación del ángulo pequeño debe calcularse en radianes.
Las tres fórmulas para la aproximación de ángulos pequeños son:
\(\sin \theta \approx \theta, \tan \theta \approx \theta ,\cos \theta \approx 1 - \frac{\theta^2}{2}\)











