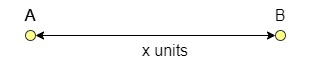Supongamos que quieres construir una valla alrededor de tu casa. Al montar esta valla de piquetes, sugieres que se construya a 6 pies del límite que rodea tu casa. A continuación se muestra un plano aproximado de este trazado.
Ejemplo 1, Aishah Amri - StudySmarter Originals
Éste es un ejemplo de locus. Observa cómo has planeado construir una valla que rodee tu casa exactamente a 1,8 m del perímetro de tu casa. Ésta es la medida estándar que deseas cumplir sobre este límite.
El locus
Para empezar este tema, establezcamos primero la definición de un lugar geométrico.
Un lugar geométrico es un conjunto de puntos que satisfacen una condición específica. El término plural para un lugar geométrico se denomina loci.
En dos dimensiones, un lugar geométrico de puntos puede representarse mediante una curva o una recta. Antes de entrar en los detalles de los tipos de loci y su construcción, definamos también el siguiente término.
Sea A un punto y B un conjunto de objetos. Si A está a distancias iguales de B, se dice que A es equidistante de B.
Tipos de loci y su construcción
En este apartado veremos cuatro tipos habituales de loci. Se enumeran a continuación.
El círculo (lugar alrededor de un punto).
La forma de salchicha (lugar alrededor de un segmento de recta).
Bisectriz perpendicular.
Bisectriz angular.
Aquí nos centraremos en dos elementos de cada uno de los locus mencionados. En primer lugar, identificaremos sus características y, en segundo lugar, aprenderemos a construirlos paso a paso.
El círculo
El círculo es un lugar geométrico de puntos que equidistan de un punto fijo, llamado centro.
La distancia fija desde el centro a cada punto del conjunto se llama radio. A continuación se muestra una representación gráfica de esta definición.
Representación gráfica de un círculo, Aishah Amri - StudySmarter Originals
Construcción
Para construir este lugar geométrico alrededor de un punto, o una circunferencia, necesitarás un compás, un lápiz y una regla. Para dibujar esta forma, también necesitarás la longitud del radio.
Paso 1: Abre el compás hasta la distancia del radio.
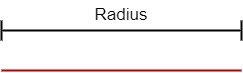
Paso 2: Coloca la punta del compás en el centro.
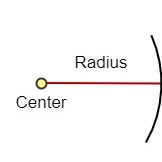
Paso 3: Dibuja un arco alrededor del centro hasta que los dos extremos se encuentren.
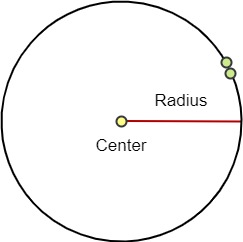
Veamos un ejemplo que aplica esta técnica.
Dado un punto, A, construye el lugar geométrico de todos los puntos que está a 2 cm de A.
Solución
Observa que aquí el radio es de 2 cm. Siguiendo los pasos anteriores, encontramos que el lugar geométrico de los puntos que están exactamente a 2 cm del punto A debe parecerse al diagrama siguiente.
Ejemplo 2, Aishah Amri - StudySmarter Originals
La forma de salchicha
Un lugar geométrico de puntos equidistantes de un segmento de recta tiene forma de salchicha. Podemos considerar este tipo de lugar geométrico como una pista que rodea a un segmento de recta.
A continuación se muestra una representación gráfica de esta definición.
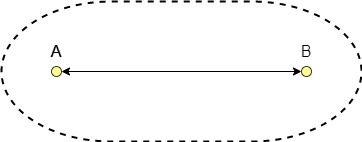
Representación gráfica de una forma de salchicha, Aishah Amri - StudySmarter Originals
Construcción
Para construir este lugar geométrico de un segmento de recta, o forma de salchicha, necesitarás un compás, un lápiz y una regla.
Paso 1: Dado un segmento de recta de longitud x unidades, marca los dos puntos extremos como A y B.
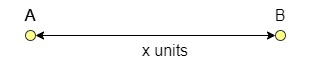
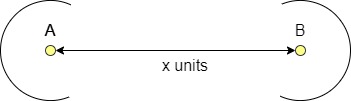
Paso 2: Abre tu compás basándote en la medida necesaria dada para formar este lugar geométrico. Dibuja un arco desde cada punto extremo A y B. Asegúrate de que esta marca forma una curva (como se muestra a continuación) que sea claramente visible.
Paso 3: Dibuja varios arcos (como se muestra a continuación) desde cualquier punto a lo largo del segmento de recta con esta medida de lugar dado. Debes hacer esto tanto para la parte superior como para la inferior del segmento de línea.
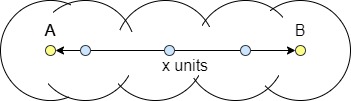
Paso 4: Utiliza tu regla para unir el punto superior de cada uno de tus arcos.
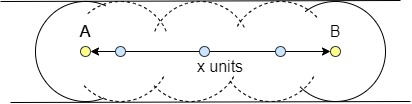
Paso5 : Al ordenar tu lugar geométrico, verás que forma una estructura parecida a una salchicha.
Veamos un ejemplo que utiliza esta técnica.
Dibuja una recta, AB, de 6 cm de longitud. Construye el lugar geométrico de todos los puntos que están a 3 cm de AB.
Solución
Empezaremos por formar la recta AB de 6 cm. Ahora, siguiendolos pasos anteriores, descubriremos que el lugar geométrico de los puntos que están exactamente a 3 cm de AB debe parecerse al siguiente esquema. Recuerda mantener el compás abierto a 3 cm en todo momento cuando construyas este lugar geométrico.
Ejemplo 3, Aishah Amri - StudySmarter Originals
La mediatriz
La mediatriz es un lugar geométrico de puntos que equidistan de dos puntos fijos. Una mediatriz divide el segmento de recta formado por esos dos puntos fijos en dos segmentos de recta menores iguales, como sugiere la palabra bisectriz.
El diagrama siguiente ilustra una mediatriz.
Representación gráfica de una bisectriz perpendicular, Aishah Amri - StudySmarter Originals
Los dos puntos fijos están representados por X e Y. La recta OM es la mediatriz del segmento de recta XY. Los puntos A, B, C y M se encuentran sobre la mediatriz y equidistan de X e Y. Por tanto, XM = YM, XA = YA, XB = YB y XC = YC. Además, OM es perpendicular a XY.
Construcción
Para construir una mediatriz, también necesitarás un compás, un lápiz y una regla.
Paso 1: Dados dos puntos A y B, traza un segmento de recta que una dichos puntos.
Paso 2: Abre el compás a más de la mitad del segmento de recta AB. Tomando A como centro, traza arcos por encima y por debajo del segmento de recta.
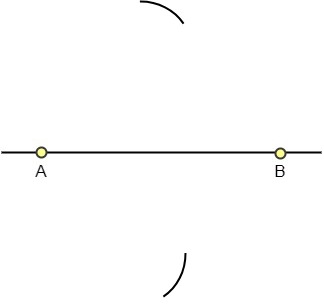
Paso 3: Repite el Paso 2, esta vez tomando B como centro. Marca los puntos de intersección como X e Y. Aquí, AX = BX y AY = BY.
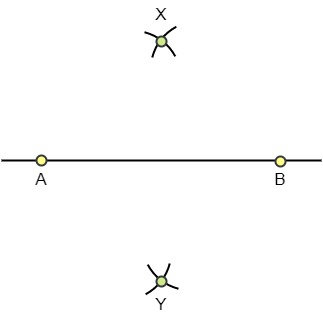
Paso4: Une los puntos X e Y. La recta XY es la mediatriz de AB.
A continuación se muestra un ejemplo que utiliza esta técnica.
Dado el rectángulo ABCD, traza una recta que corte el lado CD en dos mitades iguales.
Ejemplo 4 (1), Aishah Amri - StudySmarter Originals
Solución
Se nos dice que cortemos el lado CD en dos mitades iguales. Esto sugiere que necesitamos hallar la mediatriz de la recta CD. Siguiendo los pasos anteriores, encontramos que la mediatriz de CD divide este lado (que mide 7 cm) en dos longitudes iguales de medidas 3,5 cm cada una.
Ejemplo 4 (2), Aishah Amri - StudySmarter Originals
La bisectriz del ángulo
La bisectriz del ángulo es el lugar de los puntos que equidistan de los lados del ángulo. Como antes, el término bisectriz significa dividir un objeto en dos partes iguales. Así, la bisectriz de un ángulo da como resultado una recta que divide un ángulo en dos partes iguales.
La siguiente ilustración nos permite comprender mejor la bisectriz de un ángulo.
Representación gráfica de una bisectriz de ángulo, Aishah Amri - StudySmarter Originals
Las dos rectas fijas están representadas por los segmentos de recta AC y BC. La recta CD es la bisectriz del ángulo. La bisectriz del ángulo divide el ángulo C en dos medidas iguales, a saber, el ángulo ACD y el ángulo BCD. El punto D es equidistante de ambas rectas AC y BC. Por tanto, AD = BD. Además, AD es perpendicular a AC y BD es perpendicular a BC.
Construcción
Para construir una bisectriz de ángulo, necesitarás un compás, un lápiz y una regla.
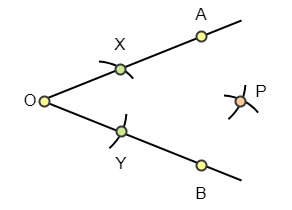
Paso 1: Dadas dos rectas OA y OB, toma O como centro y traza dos arcos tales que corten a OA y OB en los puntos X e Y respectivamente. La luz del compás debe ser menor que la distancia de OA y OB. Aquí, OX = OY.
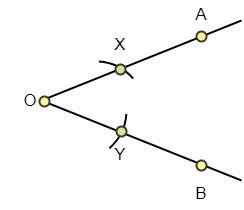
Paso2: Sin ajustar la distancia entre los catetos del compás, construye dos arcos con X e Y como centros, de forma que estos dos arcos se crucen en un punto P. Aquí, XP = YP.
Paso 3: Une los puntos OP. La recta OP es la bisectriz del ángulo O. Aquí, AP = BP y el ángulo O se divide en dos medidas iguales: Ángulo AOP y Ángulo BOP.
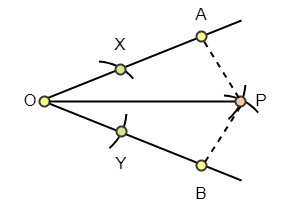
A continuación se muestra un ejemplo que aplica esta técnica.
Dado el triángulo equilátero ABC, construye la bisectriz de cada vértice e identifica el punto de intersección de las tres bisectrices.
Ejemplo 5 (1), Aishah Amri - StudySmarter Originals
Solución
En este caso, tenemos que construir la bisectriz del ángulo para cada vértice y extender la recta de modo que podamos observar dónde se cruzan estas rectas dentro del triángulo. Aplicando los pasos anteriores para cada vértice de este triángulo, encontramos que el punto en el que se cruzan las tres bisectrices de ángulos dentro del triángulo debe parecerse al dibujo de abajo. Este punto se denomina P.
Ejemplo 5(2), Aishah Amri - StudySmarter Originals
Nota: El ángulo de cada vértice de un triángulo equilátero es de 60o. Por tanto, construyendo una bisectriz de ángulo dividiremos este ángulo en dos ángulos iguales de 30o cada uno.
Ejemplo del mundo real
Terminaremos este tema con un problema del mundo real que implica la construcción de loci.
Un barco rema de modo que siempre está a la misma distancia de un puerto P y de un faro L. El puerto y el faro distan 4 km. Dibuja un diagrama a escala que muestre la distancia entre el puerto y el faro. Después, construye en el diagrama una posible trayectoria de este barco. Utiliza la escala 1 km: 1 cm.
Primero dibujaremos el segmento de recta PL. Éste representa la distancia entre el puerto y el faro.
Ejemplo 6 (1), Aishah Amri - StudySmarter Originals
Para construir una trayectoria posible para el barco, necesitamos crear una mediatriz entre el puerto y el faro. Esto se muestra a continuación.
Ejemplo 6 (2), Aishah Amri - StudySmarter Originals
El punto en el que se cruzan los dos arcos es un punto en el que el barco está a igual distancia del puerto y del faro. Lo llamaremos punto R. Une el punto P con el punto R. Haz lo mismo con los puntos L y R. El rumbo del barco seguirá una trayectoria triangular desde el puerto hasta este punto y hasta el faro. Así lo indican las flechas rojas. Esto se esboza en el diagrama siguiente.
Observa que cualquier punto de la mediatriz te da una trayectoria posible para el barco, ya que, por definición, cualquier punto de esa mediatriz es equidistante de los puntos P y R.
Ejemplo 6 (3), Aishah Amri - StudySmarter Originals
Construcción y loci - Puntos clave
Un lugar geométrico es un conjunto de puntos que siguen una regla distinta y se describe mediante una curva o una recta.
Para construir cualquier lugar geométrico, necesitarás un lápiz, una regla y un compás.
- Tipos de loci
Nombre de los loci Descripción El Círculo Locus de puntos que equidistan de un punto La forma de salchicha Lugar de los puntos que equidistan de un segmento de recta Bisectriz perpendicular Lugar de los puntos que equidistan de dos puntos Bisectriz angular Lugar de los puntos que equidistan de dos rectas
Aprende con 17 tarjetas de Construcción y Lugares Geométricos en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Construcción y Lugares Geométricos
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
