Ejemplo de señal de tráfico y papeles de colores, StudySmarter Originals
¿Ves algún parecido entre esta señal de tráfico y cada hoja de papel? De hecho, ¡hay dos semejanzas que podemos detectar aquí! En primer lugar, ambos objetos tienen exactamente cuatro lados. En segundo lugar, tienen exactamente cuatro esquinas en cada lado. Puede que ahora te estés preguntando qué tipo de forma puede tener esas propiedades y, si es así, cómo se llaman. Para responder a tu pregunta, ¡estas formas se llaman cuadriláteros!
En este debate, conoceremos un tipo concreto de polígono conocido como cuadrilátero. Veremos los distintos tipos de cuadriláteros y estudiaremos sus propiedades y las fórmulas de perímetro y área.
¿Qué es un cuadrilátero?
La abreviatura "quad" describe algo que está en términos de cuatro. Por ejemplo, una madre que lleva cuatro bebés en un embarazo estará esperando el nacimiento de cuatrillizos. En geometría, esta contracción se encuentra en el término cuadrilátero, que adopta la misma idea. Definámoslo a continuación.
Un cuadrilátero es un polígono con cuatro lados, cuatro vértices y cuatro ángulos.
Recordemos que un polígono es una figura geométrica bidimensional con un número finito de lados.
Los lados (o aristas) de un polígono están formados por segmentos de recta unidos entre sí. El punto de encuentro de un par de segmentos de recta se llama vértice (o esquina).
El término cuadrilátero procede de dos palabras latinas: quadri (una variante de cuatro) y latus (lado). Hay otros dos nombres que describen un cuadrilátero, a saber
- Un tetrágono que deriva de las palabras griegas tetra y gon que significan cuatro y ángulo (o esquina), respectivamente;
- Un cuadrilátero , ya que tiene cuatro ángulos.
Cómo nombrar un cuadrilátero
Es importante tener en cuenta el orden de los vértices de un determinado cuadrilátero a la hora de nombrarlo. He aquí un ejemplo.
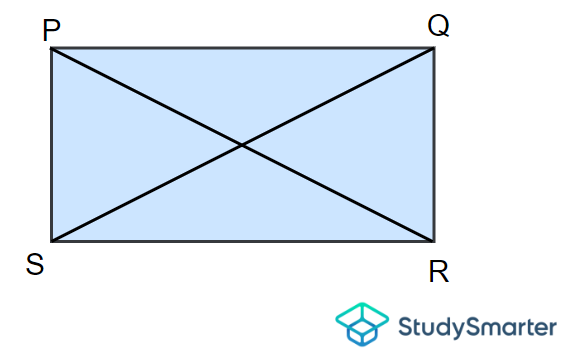
Nombrar un cuadrilátero, StudySmarter Originals
El cuadrilátero anterior tiene lados \(PQ\), \(QR\), \(RS\) y \(SP\) y vértices \(P\), \(Q\), \(R\) y \(S\). Las diagonales están descritas por \(PR\) y \(QS\).
Este cuadrilátero puede denominarse \(PQRS\), \(QRSP\), \(RSPQ\) o \(SPQR\). Sin embargo, no podemos llamarlo \(SQPR\) o \(RPQS\), por ejemplo, ya que aquí el orden de los vértices es incorrecto.
Tipos de cuadriláteros
Hay seis tipos de cuadriláteros con los que debemos familiarizarnos a lo largo de este tema. Se describen en la tabla siguiente.
Cuadrilátero | Representación visual |
Cuadrado |
Cuadrado, StudySmarter Originals |
Rectángulo, StudySmarter Originals | |
Paralelogramo |
Paralelogramo, StudySmarter Originales |
Trapecio |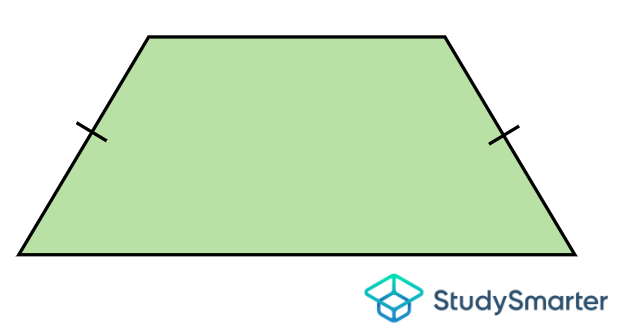
Trapecio, StudySmarter Originales |
Rombo |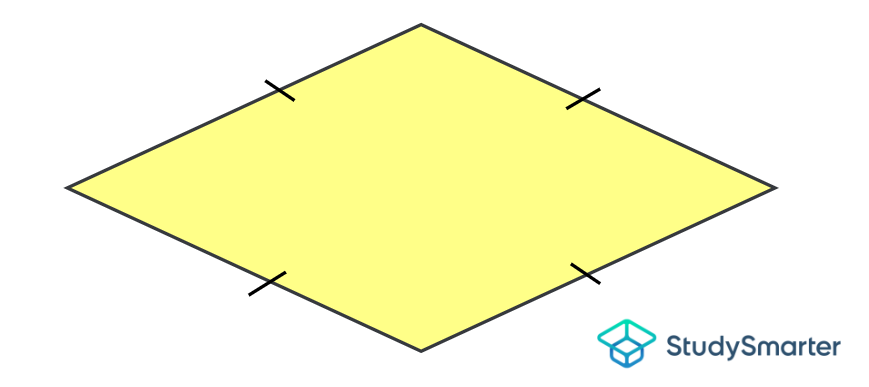
Rombo, StudySmarter Originales |
Cometa |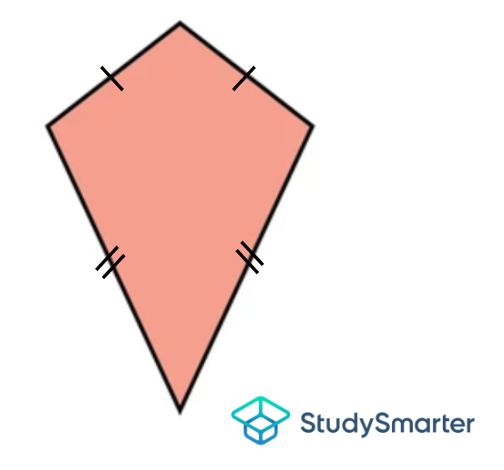
Cometa, StudySmarter Originals |
Propiedades de los cuadriláteros
Observando nuestra tabla anterior, hay cuatro características que todos los cuadriláteros tienen en común. Enumerándolas a continuación, podemos decir que todo cuadrilátero tiene
Cuatro lados;
Cuatro vértices;
Dos diagonales;
La suma de todos sus ángulos interiores es 360o.
Aunque todos los cuadriláteros tienen las mismas cualidades básicas, las medidas de sus lados y ángulos difieren entre sí. En la tabla siguiente describiremos las características distintivas de los seis cuadriláteros presentados anteriormente.
Cuadrilátero | Lados | Lados paralelos | Ángulos | Ángulos rectos | Diagonales |
Cuadrado
Cuadrado, StudySmarter Originals | Tiene 4 lados iguales | Tiene 2 pares de lados paralelos | Tiene 4 ángulos iguales | Tiene 4 ángulos rectos | Tiene 2 diagonales iguales que son perpendiculares y se bisecan entre sí |
Rectángulo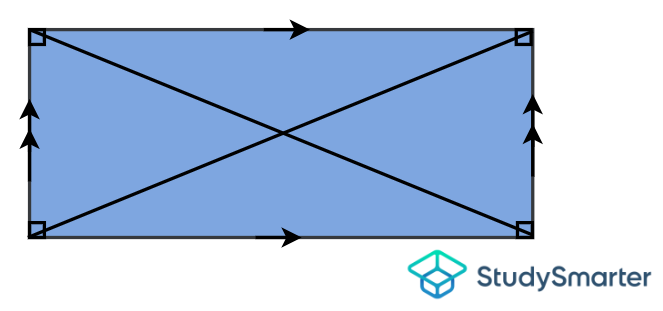
Rectángulo, StudySmarter Originals | Tiene lados opuestos de igual longitud | Tiene 2 pares de lados paralelos | Tiene 4 ángulos iguales | Tiene 4 ángulos rectos | Tiene 2 diagonales iguales que se bisecan entre sí |
Paralelogramo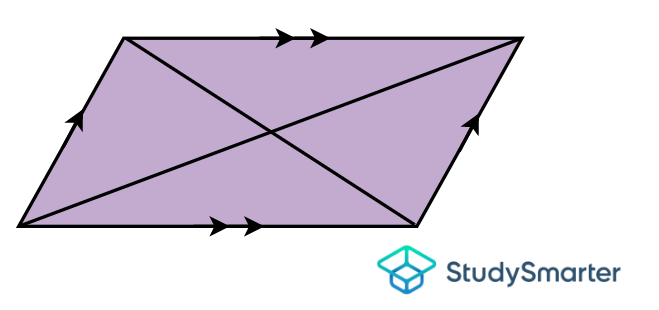
Paralelogramo, StudySmarter Originals | Tiene lados opuestos de igual longitud | Tiene 2 pares de lados paralelos | Tiene ángulos opuestos de igual medida | Ninguno | Tiene 2 diagonales no iguales que se bisecan entre sí |
Trapecio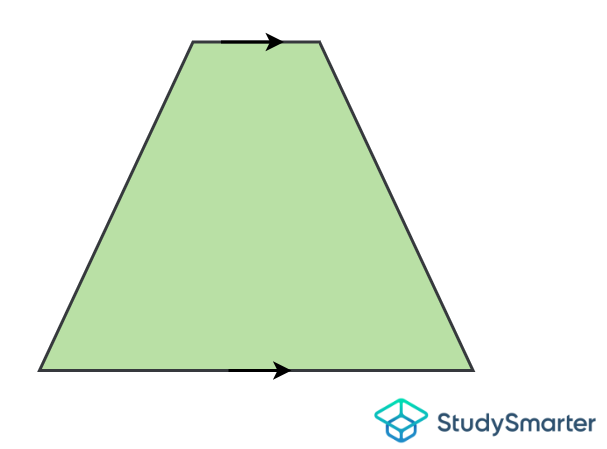
Trapecio, StudySmarter Originals |
|
|
| Si hay dos ángulos rectos adyacentes, se llama trapecio rectángulo.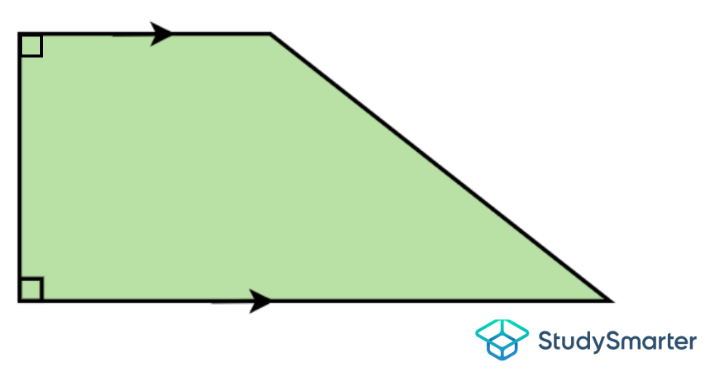
Trapecio rectángulo, StudySmarter Originals | Si las diagonales tienen la misma longitud, es un trapecio isósceles.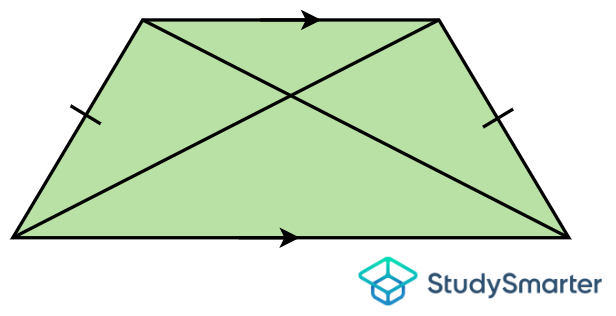
Trapecio isósceles, StudySmarter Originals |
Rombo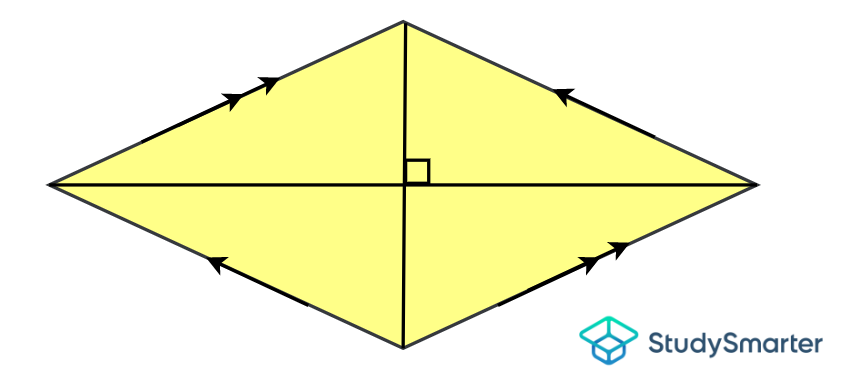
Rombo, StudySmarter Originals | Tiene 4 lados iguales | Tiene 2 pares de lados paralelos | Tiene ángulos opuestos de igual medida | Ninguno | Tiene 2 diagonales no iguales que son perpendiculares y se bisecan entre sí |
Cometa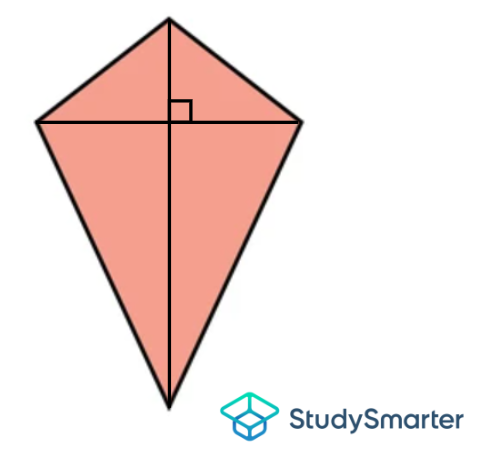
Cometa, StudySmarter Originals | Tiene dos pares de lados adyacentes iguales | Ninguno | Tiene un par de ángulos opuestos iguales que son obtusos | Ninguno | Tiene 2 diagonales no iguales que son perpendiculares y se bisecan entre sí |
Ángulos de los cuadriláteros
En este segmento trataremos las características de los ángulos interiores y exteriores de un cuadrilátero. También observaremos algunas relaciones notables entre sus ángulos opuestos y adyacentes.
Ángulos interiores de un cuadrilátero
Antes habíamos mencionado que la suma de los ángulos interiores de un cuadrilátero es \(360º\). Como un cuadrilátero es un tipo de polígono, podemos demostrar esta afirmación mediante la siguiente fórmula.
Fórmula de la suma de ángulos interiores
Para un polígono con n número de lados, la suma de sus ángulos interiores, S es igual a
\[S=(n-2)\times 180º\]
Como un cuadrilátero tiene cuatro lados, entonces \(n = 4\) y por tanto
\[S=(4-2)\times 180º\\]
\[\Nimplica que S=2\Nveces 180º]
\[\implica S=360º\]
Así, hemos demostrado que todos los ángulos interiores de un cuadrilátero suman \(360º\).
Ángulos interiores de un cuadrilátero, StudySmarter Originals
En el rectángulo anterior, \(\ángulo SPQ + \ángulo PQR + \ángulo QRS + \ángulo RSP = 360º\).
Ángulos adyacentes de cuadriláteros
Dos ángulos que están uno al lado del otro se llaman ángulos adyacentes. Los ángulos adyacentes suelen utilizar dos conceptos importantes, a saber
Ángulos suplementarios: Dos ángulos adyacentes son suplementarios cuando la suma de sus medidas es igual a \(180º\).
Ángulos complementarios: Dos ángulosadyacentes son complementarios cuando la suma de sus medidas es igual a \(90º\).
Estas dos ideas pueden aplicarse también a los cuadriláteros. Observemos el rombo que aparece a continuación.
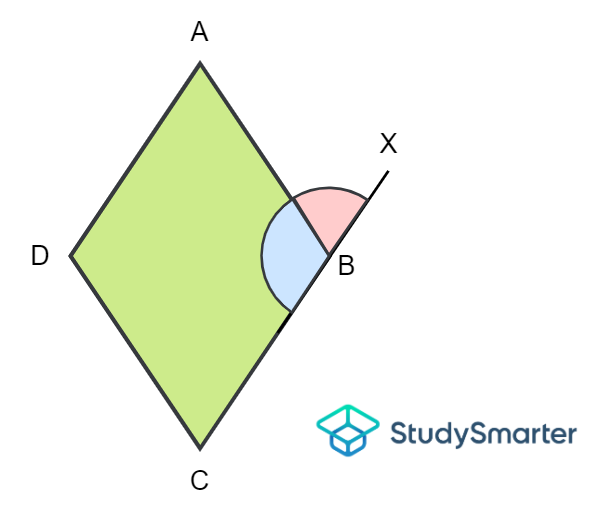
Ángulos complementarios de un cuadrilátero, StudySmarter Originals
El segmento de recta \(CBX\) está formado por \(\ángulo ABC\) (ángulo interior del rombo) y \(\ángulo ABX\) (ángulo exterior del rombo). El ángulo de una recta es siempre \(180º\). Como \(\ángulo ABC\) y \(\ángulo ABX\) se encuentran sobre esta recta y son adyacentes entre sí, son ángulos suplementarios. Supongamos que nos dan \(\ángulo CBA = 114º\). Para hallar \(\ángulo ABX\), podemos realizar el siguiente cálculo.
\[\ángulo ABC + \ángulo ABX=\ sobrelínea{CBX}\]
\[\implica \ángulo ABC+114º=180º\]
\[Implica que el ángulo ABC=180º-114º]
\[Implica que el ángulo ABC = 66º]
Por tanto, \(\ángulo ABX=66º\). Ahora, echemos un vistazo al rectángulo de abajo.
Ángulos complementarios de un cuadrilátero, StudySmarter Originals
Dadas las propiedades de un rectángulo, sabemos que cada ángulo interior es \(90º\). Digamos que \(\ángulo RSQ = 22º\). Ahora debemos hallar \(\ángulo PSQ\). Para ello, basta con observar que la suma de \(\ángulo RSQ) y \(\ángulo PSQ) es igual a \(90º\), ya que son adyacentes y forman un ángulo recto. Por tanto, \(\ángulo PSQ\) es \(68º\) ya que
\[\ángulo PSQ + \ángulo RSQ=\ángulo PSR\]
\[\implica \ángulo PSQ+22º=180º\\]
\[\implica \ángulo PSQ=180º-22º\]
\[\implica \ángulo PSQ=68º\]
Ángulos exteriores de un cuadrilátero
La suma de los ángulos exteriores de cualquier polígono es igual a \(360º\). Esto significa que la suma de los ángulos exteriores de un cuadrilátero también es \(360º\). Para demostrarlo, volvamos a nuestro rectángulo anterior y tracemos una recta prolongada en cada vértice.
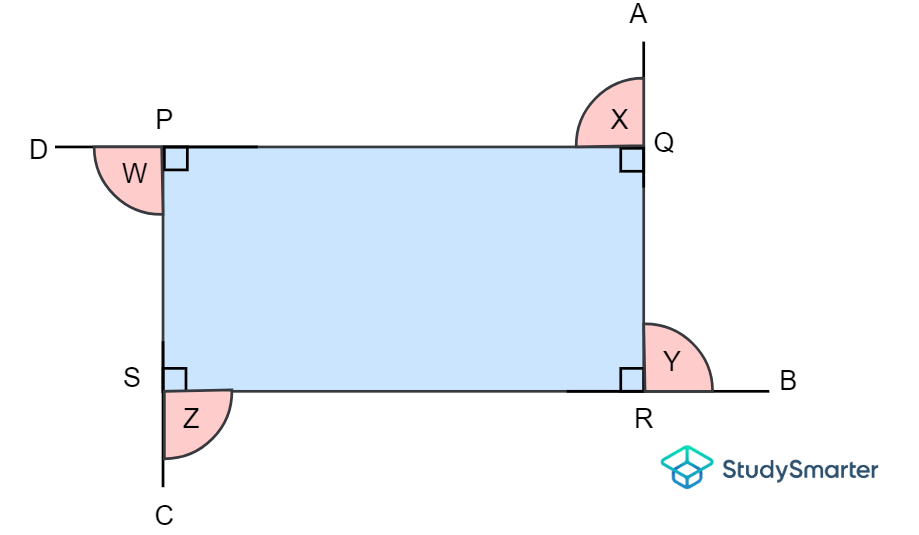
Ángulos exteriores de un cuadrilátero, StudySmarter Originals
Los ángulos interiores de este rectángulo son \(\ángulo SPQ\), \(ángulo PQR\), \(\ángulo QRS\) y \(\ángulo RSP\), mientras que los ángulos exteriores son \(\ángulo W\), \(\ángulo X\), \(\ángulo Y\) y \(\ángulo Z\). Observa que a cada ángulo interior le corresponde un ángulo exterior que es adyacente a ellos y se encuentra en una recta. Recuerda que el ángulo de una recta es \(180º\). Así pues, tenemos cuatro conjuntos de ángulos suplementarios. En este caso, los ángulos exteriores también son iguales, ya que los interiores son todos iguales. Resolvamos uno de estos ángulos exteriores para demostrar nuestra afirmación.
\[\ángulo PQR=\ángulo X=\línea superior{RQA}\]
\[\implica \ángulo PQR+90º=180º\]
\[\implica \ángulo PQR=180º-90º\]
\[\implica \ángulo PQR=90º\]
Como \(\ángulo X = \ángulo Y = \ángulo Z = \ángulo W= 90º\), entonces \(\ángulo X + \ángulo Y + \ángulo Z + \ángulo W = 9(90º)= 360º\), como es debido.
Ángulos verticalmente opuestos de cuadriláteros
Losángulosverticalmente opuestos son dos ángulos (opuestos) construidos por dos rectas que se cruzan y salen de un par de vértices distintos. Los ángulos verticalmente opuestos son siempre iguales entre sí. Volvamos a nuestro rectángulo anterior, en el que O es el punto de intersección entre las dos diagonales.
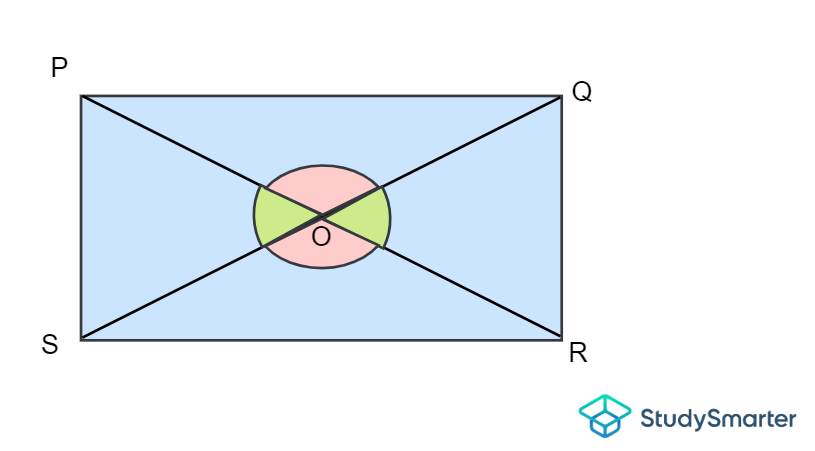
Ángulos verticalmente opuestos de un cuadrilátero, StudySmarter Originals
Aquí, \(\ángulo POQ\) y \(\ángulo SOR\) son ángulos verticalmente opuestos. Por tanto, \(\ángulo POQ = \ángulo SOR\). Del mismo modo, \(\ángulo POS\) y \(\ángulo QOR\) son ángulos verticalmente opuestos, por lo que \(\ángulo POS =\ángulo QOR\). El mismo concepto se aplica a cuadrados, rectángulos, paralelogramos, rombos y cometas (¡pruébalo tú mismo!).
Ángulos correspondientes de los cuadriláteros
Losángulos correspondientes se forman cuando dos rectas paralelas son intersecadas por la recta transversal. Una recta transversal es una recta que cruza un par de rectas en el mismo plano en dos puntos concretos. Los ángulos correspondientes son siempre iguales entre sí. Mostrémoslo con el paralelogramo siguiente.
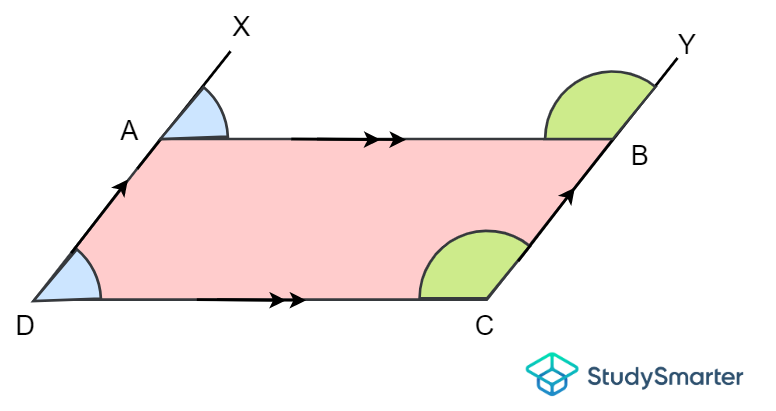
Ángulos correspondientes de un cuadrilátero, StudySmarter Originals
Aquí, \(\ángulo ADC\) (ángulo interior del paralelogramo) y \(\ángulo XAB\) (ángulo exterior del paralelogramo) son ángulos correspondientes, ya que la recta \(DAX\) pasa por los lados paralelos \(AB\) y \(DC\). Por tanto, \(\ángulo ADC = \ángulo XAB\).
Análogamente, \(\ángulo BCD\) y \(\ángulo YBA\) son ángulos correspondientes, ya que la recta \(CBY\) atraviesa los lados paralelos \(AD\) y \(BC\). Por tanto, \(\ángulo BCD = \ángulo YBA\). Este concepto se aplica también a cuadrados, rectángulos y rombos (¡haz la prueba!).
Perímetro de los cuadriláteros
El perímetro de un cuadrilátero se define como la longitud total de sus límites. En otras palabras, es la suma de todos sus lados. Por tanto, para un cuadrilátero \(ABCD\)
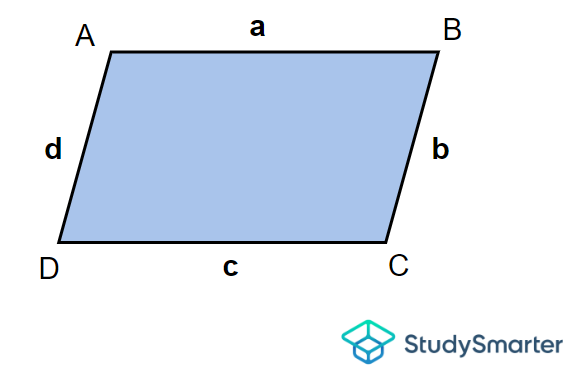
El perímetro de los cuadriláteros, StudySmarter Originals
con lados \(AB\), \(BC\), \(CD\) y \(DA\), el perímetro, \(P\) es
\[P=\overline{AB}+\overline{BC}+\overline{CD}+\overline{DA}\]
o
\[P=a+b+c+d\]
He aquí dos ejemplos.
Halla el perímetro del paralelogramo siguiente.
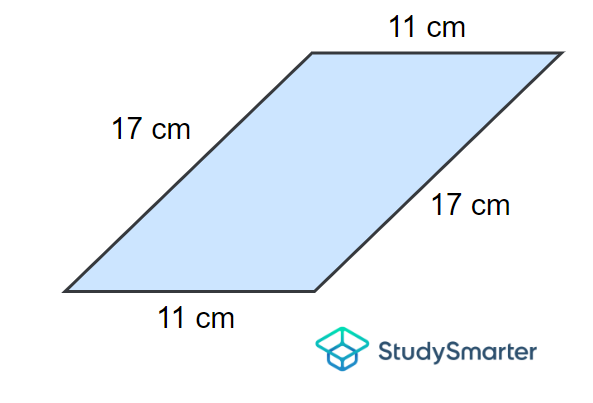
Ejemplo 1, StudySmarter Originals
Solución
Para resolverlo, simplemente sumaremos las dimensiones de los cuatro lados de este paralelogramo.
\[P=17+17+11+11\]
\[\implica P=2(17)+2(11)\]
\[\implica P=34+22\]
\[implica que P = 56 cm].
Por tanto, su perímetro es \(56 \mathrm{cm}).
Calcula la longitud del lado que falta, \(x\) del trapezoide de abajo, dado que el perímetro es \(51\,\mathrm{cm}).
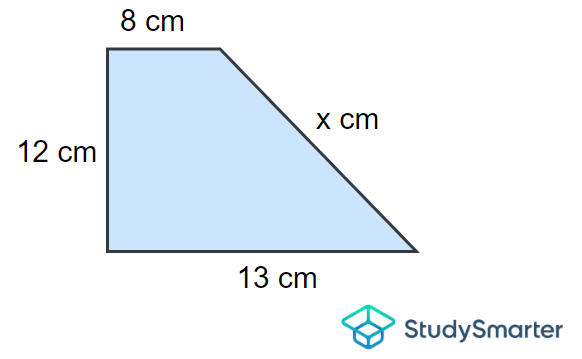
Ejemplo 2, StudySmarter Originals
Solución
Utilizando la fórmula del perímetro de un cuadrilátero, hallamos que
\[P=8+12+13+x\\]
\[\implica 51=8+12+13+x\]
\[\implica 8+12+13+x=51\]
Llevando ahora \(8\), \(12\) y \(13\) al lado derecho de esta ecuación, convirtiendo así \(x\) en sujeto, obtenemos
\[x=51-8-12-13\]
\[\implica x=18\,\mathrm{cm}]
Por tanto, la longitud del lado que falta, \(x\) es \(18\, \mathrm{cm}\).
Área de los cuadriláteros
El área de un cuadrilátero viene descrita por el espacio comprendido dentro de sus límites. Cada uno de los seis tipos de cuadriláteros que hemos visto anteriormente tiene su propia fórmula de área. La tabla siguiente presenta sus respectivas fórmulas de área.
Cuadrilátero | Área |
Cuadrado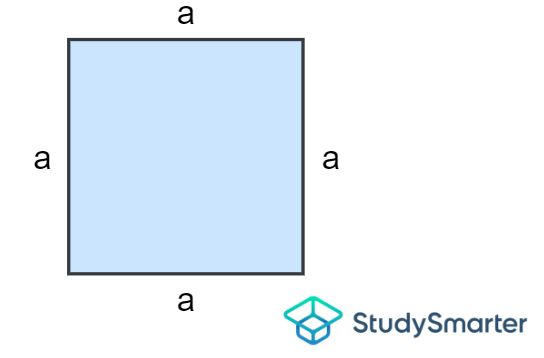
Área de un cuadrado, StudySmarter Originals | \[A=a\times a=a^2\] donde \(a\) es la longitud de cada lado. |
Rectángulo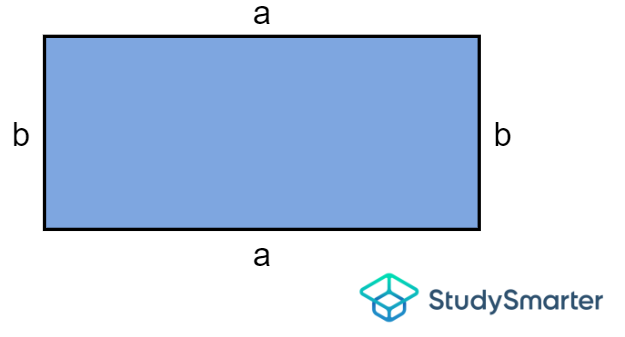
Área de un rectángulo, StudySmarter Originals | \[A=a\times b\] donde \(a\) y \(b\) son las longitudes de la anchura y la altura, respectivamente. |
Paralelogramo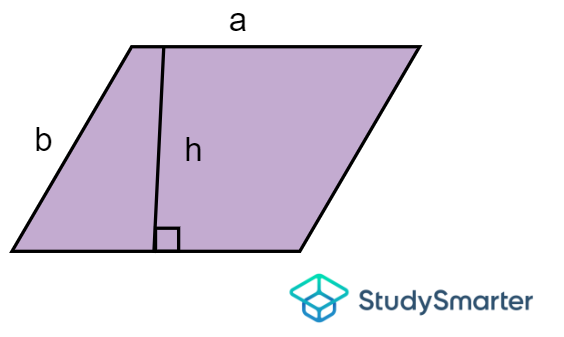
Área de un paralelogramo, StudySmarter Originals | \[A=a\times h\] donde \(a\) y \(h\) son las longitudes de anchura y altura, respectivamente. |
Trapecio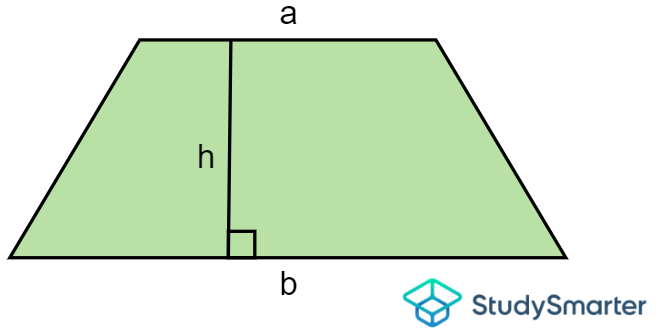
Área de un trapecio, StudySmarter Originals | \[A=\dfrac{1}{2} veces (a+b)\ veces h\] donde \(a\) y \(b\) son las longitudes de las bases (lados paralelos superior e inferior) y h es la altura. |
Rombo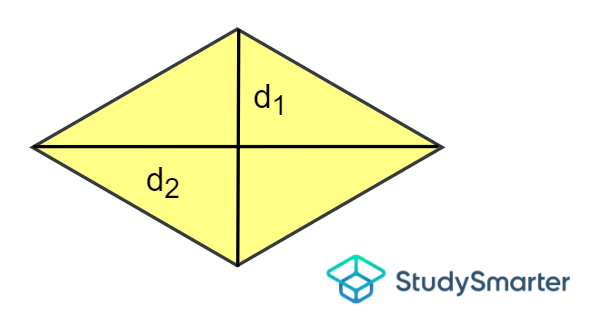
Área de un rombo, StudySmarter Originals | \[A=\dfrac{1}{2} veces d_1\ veces d_2\] donde \(d_1\) y \(d_2\) son las longitudes de la diagonal vertical y la diagonal horizontal, respectivamente. |
Cometa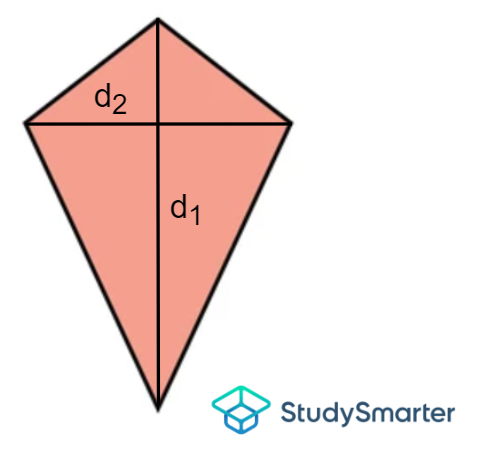
Área de una cometa, StudySmarter Originals | \[A=\dfrac{1}{2} veces d_1\ veces d_2\] donde d1 y d2 son las longitudes de la diagonal vertical y la diagonal horizontal, respectivamente. |
Veamos dos ejemplos trabajados.
Halla el área del trapecio siguiente.
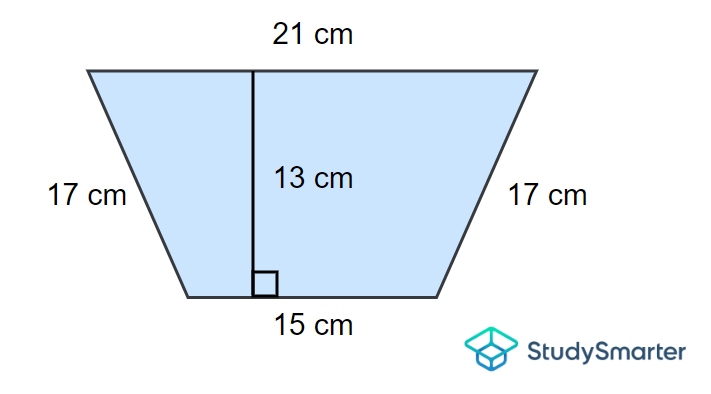
Ejemplo 3, StudySmarter Originals
Solución
Del diagrama anterior podemos deducir que
\[a = 21\, \mathrm{cm}\]
\[b = 15\, \mathrm{cm}\]
\[h = 13\, \mathrm{cm}]
Utilizando ahora la fórmula del área de un trapecio, obtenemos
\A=dfrac{1}{2}veces (21+15)|veces 13\].
\A=dfrac1/2 veces (36)13 veces].
\A = veces 468]
\[\implies A=234\,\mathrm{cm}^2\]
Nota importante: ¡no te dejes confundir por la longitud de las bases y los catetos! Los lados paralelos son las bases, que son las que utilizaremos en nuestra fórmula.
Por tanto, el área es \(234\, \mathrm{cm}^2\).
Halla la longitud de la diagonal horizontal, d, del rombo de abajo, dado que el área es \(123,5, \mathrm{cm}).
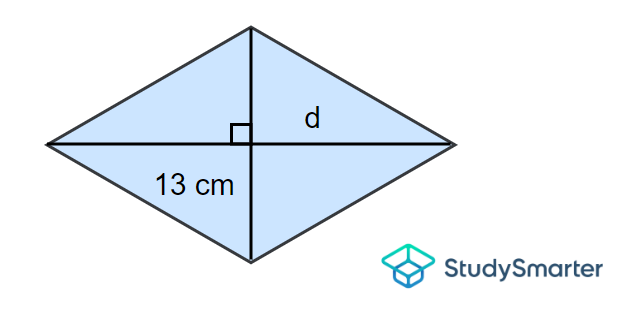
Ejemplo 4, StudySmarter Originals
Solución
Aquí, la diagonal vertical es \(13\,\mathrm{cm}\). Utilizando la fórmula del área de un rombo, hallamos que
\[A=\dfrac{1}{2}veces 13\veces d\}]
\[Aplica 123,5=\dfrac{1}{2}veces 13veces d\]
\[Implica que 123,5=123,5]
Multiplicando ahora ambos lados por \(2\), obtenemos
\[\cancel{2}\left(\dfrac{13\times d}{\cancel{2}}\right)=2(123.5)\]
\[|implica 13d=247\]
Entonces, dividiendo ambos lados por \(13\), obtenemos
\[\dfrac{\cancel{13}d}{\cancel{13}}=\dfrac{247}{13}\]
\[\implica d=19\,\mathrm{cm}]
Por tanto, la longitud de la diagonal horizontal, \(d\) es \(19\, \mathrm{cm}\).
Ejemplos de cuadriláteros
Terminaremos este tema con varios ejemplos trabajados de cuadriláteros que hacen uso de los conceptos que hemos establecido a lo largo de esta discusión.
Dada la cometa \(ABCD\) que aparece a continuación, responde a las siguientes preguntas:
Halla los lados que faltan \(AD\) y \(AB\), dado que el perímetro es \(88\,\mathrm{cm}).
Calcula los ángulos que faltan \(M\) y \(N\).
¿Alguno de estos lados es paralelo?
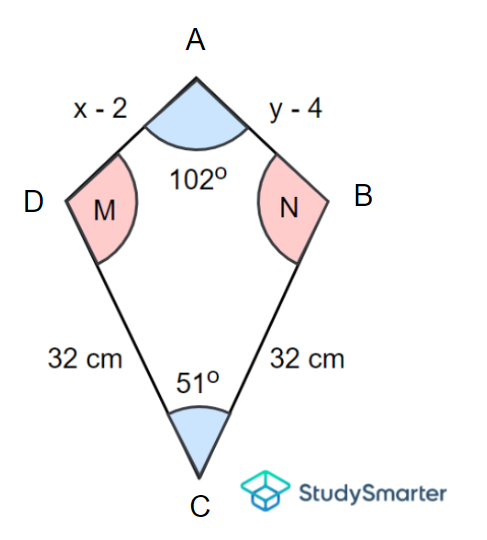
Ejemplo 5, StudySmarter Originals
Pregunta 1
En primer lugar, observa que \(AD = AB\) ya que una cometa tiene dos pares de lados adyacentes iguales (el otro es \(CB = CD\)).
\[AD=AB\]
\[\implica x-2=y-4\]
\[\implica y=x-2+4\]
\[|implica y=x+2\]
Ahora, dado el perímetro y la suma de todos sus lados, obtenemos
\P=AB+AD+CD+CD\]
\[\implies 88=(y-4)+(x-2)+32+32\]
\[\implica 88=y+x-6+64\]
Sustituyendo ahora por \(y\) y resolviendo esta ecuación para \(x\), obtenemos
\[88=(x+2)+x-6+64\]
\[\implica (x+2)+x-6+64=88\]
\[|implica 2x+60=88\]
\[Implica 2x=88-60]
|[|implica 2x=28\]
Dividiendo ahora ambos lados por \(2\), tenemos
\x=dfrac{28}{2}]
|[|implica x=14\]
Por tanto, las longitudes de \(AB\) y \(AD\) son
\[AB=y-4\]
\[implica AB=(x+2)-4]
\[implica que AB=(14+2)-4]
\[\implies AB=12\,\mathrm{cm}\]
Como \(AB = AD\), entonces \(AD\) es también \(12\, \mathrm{cm}\).
Pregunta 2
Recuerda que una cometa tiene un par de ángulos opuestos iguales que son obtusos. Esto significa que \(M = N\). Además, que las medidas de los otros dos ángulos están dadas y la suma de todos los ángulos interiores de cualquier cuadrilátero es \(360º\). A partir de aquí, encontramos que
\[\ángulo DAB+ángulo BCD+ángulo M+ángulo N=360º\]
\[\implica 102º+51+\ángulo M+\ángulo N=360º\]
\implica 153º+2\ángulo M=360º\]
Resolviendo ahora para \(M\), obtenemos
\[2\ángulo M=360º-153º\]
\[\implica 2\ángulo M=207º\]
\[\implica \ángulo M=\dfrac{207º}{2}\]
\[Implica el ángulo M=103,5º]
Por tanto, tanto \(M\) como \(N\) son iguales a \(103,5º) (ya que \(M = N\)).
Pregunta 3
Por las propiedades de una cometa, no hay lados que sean paralelos entre sí.
Dado el paralelogramo \(ABCD\) que aparece a continuación, responde a las siguientes preguntas:
Halla la longitud de \(AB\) dado que el perímetro es \(40\, \mathrm{cm}\).
Calcula el área de \(ABCD\).
Deduce el ángulo \(Y\).
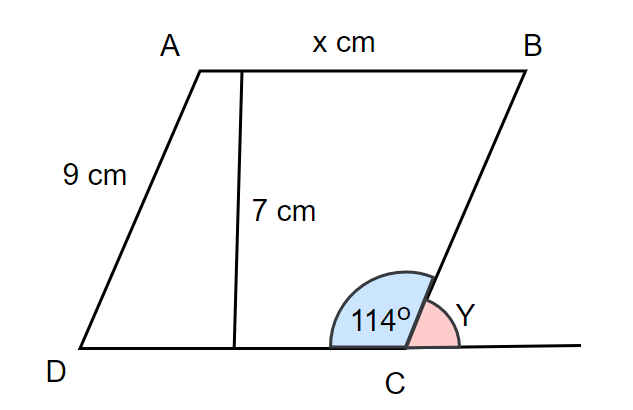
Ejemplo 6, StudySmarter Originals
Pregunta 1
En primer lugar, observa que \(AB = DC\) y \(AD = BC\) ya que un paralelogramo tiene dos pares de lados opuestos iguales. Dado el perímetro y la suma de todos sus lados, obtenemos
\[P=AB+AD+CD+CD\]
\[\implica 40=x+9+x+9\]
\[\implica 40=2x+18\]
Resolviendo ahora esta ecuación para \(x\), obtenemos
\[2x=40-18\]
\[|implica 2x=22\]
\[|implica x=\dfrac{22}{2}]
\[Supone x=11,5cm]
Por tanto, la longitud de \(AB\) es \(11\, \mathrm{cm}\).
Pregunta 2
Aquí, la altura es \(7\, \mathrm{cm}) y la anchura es la longitud del lado \(AB\). Sabemos que \(AB\\) es igual a \(11\, \mathrm{cm}\). Así, por la fórmula del área de un paralelogramo, tenemos
\A = 11 veces 7].
\[|implica 77\,\mathrm{cm}^2]
Por tanto, el área de (ABCD) es (77).
Pregunta 3
En este caso, \(\ángulo BCD\) y \(\ángulo Y\) son suplementarios, ya que ambos ángulos están sobre una recta. Recuerda que dos ángulos son suplementarios cuando la suma de sus medidas es igual a \(180º\). Utilizando esta idea, encontramos que
\[\ángulo BCD+\ángulo Y=180º\\]
\[\implica 114º+\ángulo Y=180º\]
Ahora, reordenando esta ecuación y resolviendo para nuestro ángulo que falta, obtenemos
\[\ángulo Y=180º-114º\]
\[\implica \ángulo Y=66º\]
Así pues, \(Y\) es igual a \(66º\).
Dado el rectángulo \(PQRS\) que aparece a continuación, responde a las siguientes preguntas:
Halla el perímetro y el área de \(PQRS\).
Calcula la longitud de la diagonal \(QS\).
¿Cuánto mide \(\ángulo QSR\)?
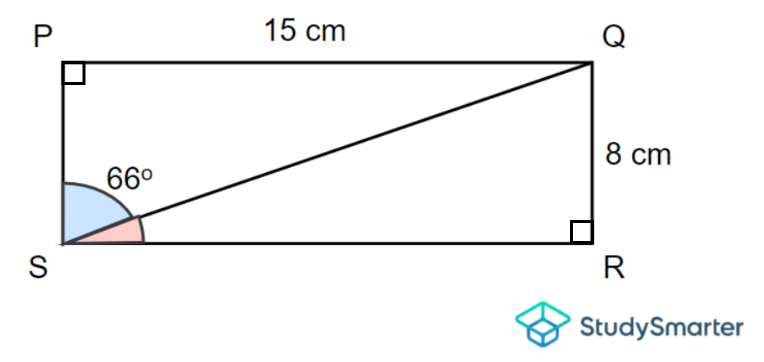
Ejemplo 7, StudySmarter Originals
Pregunta 1
En primer lugar, observa que \(PQ = SR\) y \(PS = QR\) ya que un rectángulo tiene dos pares de lados opuestos iguales. Ahora, sumando las longitudes de todos sus lados, obtenemos
\[P=PQ+QR+SR+PS\]
\[\implica P=15+8+15+8\]
\[\implica P=46\,\mathrm{cm}]
Aquí, la longitud es \(15,\mathrm{cm}) y la altura es \(8,\mathrm{cm}). Por tanto, según la fórmula del área de un rectángulo, resulta que
\[A=15\tiempos 8\]
\[\implies A=120\,\mathrm{cm}^2\]
Por tanto, el perímetro es \(46\,\mathrm{cm}) y el área es \(120\,\mathrm{cm}^2).
Pregunta 2
Por las propiedades de un rectángulo, recuerda que tiene 4 ángulos rectos. Observa que la diagonal \(QS\) crea un triángulo rectángulo \(QRS\) donde \(\ángulo QRS\) es igual a \(90º\). Por tanto, podemos utilizar el Teorema de Pitágoras para hallar la longitud de \(QS\). Aquí, \(QS\) es la hipotenusa y los dos lados son \(QR = 8 \,\mathrm{cm}\) y \(SR = 15\,\mathrm{cm}\). Al hacerlo, obtenemos
\[QS^2=QR^2+SR^2\]
\[\implica QS^2=8^2+15^2\2]
\[\implica QS^2=64+225\]
\[|implica QS^2=289\]
Sólo consideraremos la raíz positiva, ya que se trata de medidas. Entonces
\[QS=\sqrt{289}\]
\[\implies QS=17\,\mathrm{cm}\]
Por tanto, la diagonal, \(QS\) es igual a \(17\,\mathrm{cm}\).
Pregunta 3
Aquí, \(\ángulo PSQ\) y \(\ángulo QSR\) son complementarios, ya que estos dos ángulos se encuentran en un ángulo recto. Recordemos que dos ángulos son complementarios cuando la suma de sus medidas es igual a \(90º\). Por tanto, tenemos
\[\ángulo PSQ+\ángulo QSR=90º\]
\[\implica 66º+\ángulo QSR=90º\]
Ahora, reordenando esta ecuación y resolviendo el ángulo que nos falta, obtenemos
\[\ángulo QSR=90º-66º\]
\[\implica \ángulo QSR=24º\]
Así pues, \(\ángulo QSR\) es igual a \(24º\).
Cuadriláteros - Puntos clave
- Un cuadrilátero es un polígono con cuatro lados, cuatro vértices y cuatro ángulos.
- Un cuadrilátero tiene dos diagonales.
- La suma de todos los ángulos interiores de un cuadrilátero es \(360º\).
- Hay seis tipos de cuadriláteros: cuadrado, rectángulo, paralelogramo, trapecio, rombo y cometa.
- El perímetro de un cuadrilátero es la suma de todos sus lados, es decir, \(P = a + b + c + d\)
- Fórmula del área de los cuadriláteros
Cuadrilátero
Área
Cuadrado
\(A=a\times a=a^2\)
Rectángulo
\(A = a = veces b)
Paralelogramo
\(A = a veces h)
Trapecio
\Trapecio (A=drac1/2 veces (a+b)veces h)
Rombo
\(A = d_1 veces d_2 veces d_2)
Cometa
\(A=dfrac12veces d1veces d2)
Aprende con 0 tarjetas de Cuadriláteros en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Cuadriláteros
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
