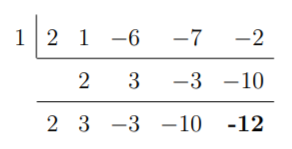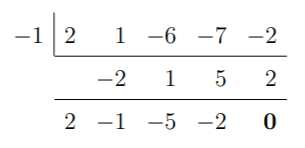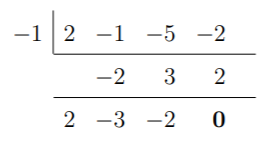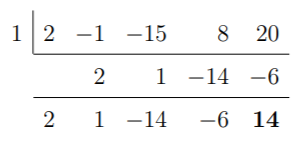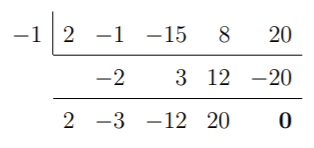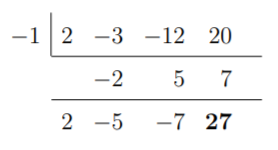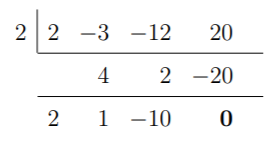Encontrar ceros racionales: Métodos, Ejemplos

Saltar a un capítulo clave

$2 x y^{4} - 14 x^{3} y^{2} + 8 x y - 6 x^{2} y^{3} = 0$

Esta expresión parece bastante complicada, ¿verdad? Tratar con polinomios largos puede ser bastante engorroso y puede dar lugar a algunos errores por descuido no deseados. Sin embargo, existe una solución para este problema. ¿Adivinas cuál puede ser? Déjame darte una pista: ¡es la factorización!

Hasta ahora hemos estudiado varios métodos para factorizar polinomios, como la agrupación, el reconocimiento de productos especiales y la identificación del máximo común divisor. En este artículo hablaremos de otra técnica de factorización de polinomios llamada búsqueda de ceros racionales.

Ceros racionales

En este apartado nos proponemos encontrar los ceros racionales de los polinomios introduciendo el Teorema de los Ceros Racionales. El objetivo de este tema es establecer otro método de factorización y resolución de polinomios mediante el reconocimiento de las raíces de una ecuación dada. Definamos primero los términos que aparecen a continuación.

Un cero de un polinomio está definido por todos los valores x que hacen que el polinomio sea igual a cero. También se conoce como raíz de un polinomio.

Un ceroracional es un número racional que es raíz de un polinomio que puede escribirse como fracción de dos enteros.

Para mayor claridad, definiremos también un cero irracional como un número que no es racional y se representa mediante un decimal infinito no repetido.

Además, recuerda la definición de la forma estándar de un polinomio.

Sea f un polinomio de la forma

$f (x) = a_{n} x^{n} + \dots + a_{1} x + a_{0}$ ,

donde $a_{n}, . . ., a_{0}$ son los coeficientes de las variables $x^{n}, . . ., x^{0}$ respectivamente.

Teorema de los ceros racionales

Si el polinomio f tiene coeficientes enteros, entonces todo cero racional de f, f(x) = 0, puede expresarse de la forma $\frac{p}{q}$ con q ≠ 0, donde

p es el factor del término constante de f, _a0;
q es el factor del coeficiente principal de f,_an.

Es importante factorizar el máximo común divisor (MCC) del polinomio antes de identificar las posibles raíces racionales.

Es importante tener en cuenta que el Teorema del Cero Racional sólo se aplica a los ceros racionales. No todas las raíces de un polinomio se encuentran utilizando la divisibilidad de sus coeficientes.

Aplicación del Teorema de los Ceros Racionales

En este apartado aplicaremos el Teorema de los Ceros Racionales. Demostraremos varios ejemplos prácticos que ejercitan este concepto.

Encontrar los posibles ceros racionales de un polinomio

Aquí sólo vamos a enumerar todas las posibles raíces racionales de un polinomio dado. No es necesario identificar el conjunto correcto de ceros racionales que satisfacen un polinomio. Esto se hará en el siguiente apartado. El objetivo aquí es proporcionar una idea general del Teorema de los Ceros Racionales.

Utiliza el Teorema de los Ceros Racionales para determinar todos los posibles ceros racionales del siguiente polinomio

$f (x) = 3 x^{4} + 7 x^{3} - 6$ .

Solución

Paso 1: Empezamos identificando todos los valores posibles de p, que son todos los factores de $a_{0} = 6$ .

Por tanto, p puede ser $\pm 1, \pm 2, \pm 3 o r \pm 6$ .

Paso 2 : A continuación, identificaremos todos los valores posibles de q, que son todos los factores de $a_{n} = 3$ .

Por tanto, q puede ser $\pm 1 o r \pm 3$ .

Paso 3: Encuentra los posibles valores de $\frac{p}{q}$ enumerando las combinaciones de los valores encontrados en el Paso 1 y en el Paso 2. De ello se deduce que $\frac{p}{q}$ es de la forma $\frac{f a c t o r s o f p}{f a c t o r s o f q}$ .

Por tanto $\frac{p}{q}$ puede adoptar las formas :

\pm \frac{1}{1}, \pm \frac{2}{1}, \pm \frac{3}{1}, \pm \frac{6}{1}, \pm \frac{1}{3}, \pm \frac{2}{3}, \pm \frac{3}{3}, \pm \frac{6}{3}

Paso 4: Simplificando la lista anterior y eliminando los resultados duplicados, obtenemos los siguientes posibles ceros racionales de f:

\frac{p}{q} = \pm 1, \pm 2, \pm 3, \pm 6, \pm \frac{1}{3}, \pm \frac{2}{3}

Los números anteriores son sólo los posibles ceros racionales de f.

Utiliza el Teorema de los Ceros Racionales para encontrar todas las raíces racionales posibles del siguiente polinomio

$f (x) = 15 x^{5} + 6 x^{3} - 21 x^{3} + 12$ .

Solución

Paso 1: Primero observa que podemos factorizar 3 a partir de f. Por tanto,

$f (x) = 3 (5 x^{5} + 2 x^{3} - 7 x^{3} + 4)$ .

Paso 2: A continuación, identifica todos los valores posibles de p, que son todos los factores de $a_{0} = 4$ .

Por tanto, p puede ser $\pm 1, \pm 2, o r \pm 4$ .

Paso 3 : A continuación, identificaremos todos los valores posibles de q, que son todos los factores de $a_{n} = 5$ .

Por tanto, q puede ser $\pm 1 o r \pm 5$ .

Paso 4 : Encuentra los posibles valores de $\frac{p}{q}$ enumerando las combinaciones de los valores encontrados en el Paso 1 y el Paso 2.

Así $\frac{p}{q}$ puede adoptar las formas:

$\pm \frac{1}{1}, \pm \frac{2}{1}, \pm \frac{4}{1}, \pm \frac{1}{5}, \pm \frac{2}{5}, \pm \frac{4}{5}$

Paso5: Simplificando la lista anterior y eliminando los resultados duplicados, obtenemos los siguientes posibles ceros racionales de f:

$\frac{p}{q} = \pm 1, \pm 2, \pm 4, \pm \frac{1}{5}, \pm \frac{2}{5}, \pm \frac{4}{5}$

Encontrar los ceros racionales de un polinomio

Aquí determinaremos el conjunto de ceros racionales que satisfacen el polinomio dado. Al hacerlo, podremos factorizar el polinomio y resolver la expresión en consecuencia. A continuación se indican los pasos principales para llevar a cabo este proceso:

Paso1 : Enumera todos los ceros posibles utilizando el Teorema de los Ceros Racionales.

Paso2: Aplica la división sintética para calcular el polinomio en cada valor de los ceros racionales hallados en el Paso 1. Asegúrate de anotar el cociente obtenido si el resto es 0.

Paso 3: Repite los Pasos 1 y 2 para el cociente obtenido. Detente cuando hayas obtenido un cociente que sea cuadrático (polinomio de grado 2) o que se pueda factorizar fácilmente.

Paso 4: Establece todos los factores iguales a cero y resuelve o utiliza la fórmula cuadrática para evaluar las soluciones restantes.

Veámoslo con algunos ejemplos prácticos.

Encuentra todos los ceros racionales del polinomio

$f (x) = 2 x^{4} + x^{3} - 6 x^{2} - 7 x - 2$ .

Paso 1: Utilizando el Teorema de los Ceros Racionales, enumeraremos todos los posibles ceros racionales de la forma $\frac{p}{q}$ .

Aquí, p debe ser un factor de $a_{0} = 2$ y q debe ser un factor de $a_{n} = 2$ .

Por tanto, los posibles ceros racionales de f son: $\pm 1, \pm 2 o r \pm \frac{1}{2}$ .

Paso 2: Aplicando la división sintética, debes calcular el polinomio en cada valor de los ceros racionales encontrados en el Paso 1. Si obtenemos un resto de 0, entonces se ha encontrado una solución. Empezaremos con +1.

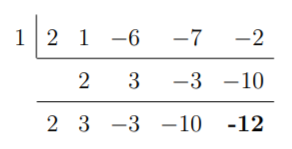
Aquí, vemos que +1 da un resto de -12. Por tanto, no es una raíz de f(x). Probemos con -1.

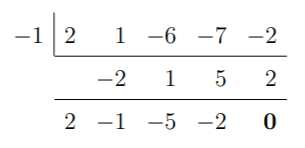
En este caso, -1 da un resto de 0. Por tanto, -1 es una solución de f. El resultado de esta división sintética también nos dice que podemos factorizar f como:

$f (x) = (x + 1) (2 x^{3} - x^{2} - 5 x - 2)$

Paso 3: A continuación, repite este proceso en el cociente:

2 x^{3} - x^{2} - 5 x - 2

Utilizando el Teorema de los Ceros Racionales, los posibles, los posibles ceros racionales de este cociente son:

$\pm 1, \pm 2 o r \pm \frac{1}{2}$

Como hemos demostrado que +1 no es una solución de f, no necesitamos volver a comprobarlo. Sin embargo, debemos aplicar de nuevo la división sintética a -1 para este cociente. Esto mostrará si hay alguna multiplicidad de una raíz dada.

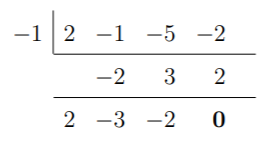
De nuevo, vemos que -1 da un resto de 0 y, por tanto, es una raíz del cociente. Esto demuestra que la raíz -1 tiene una multiplicidad de 2. Por tanto, f se factoriza además como

$f (x) = (x + 1) (x + 1) (2 x^{2} - 3 x - 2) = {(x + 1)}^{2} (2 x^{2} - 3 x - 2)$

Paso 4: Obtenemos el cociente:

$2 x^{2} - 3 x - 2$

que es, efectivamente, una ecuación cuadrática que podemos factorizar como:

$(2 x + 1) (x - 2)$

Esto demuestra que las soluciones restantes son:

$x = - \frac{1}{2} a n d x = 2$

La expresión totalmente factorizada de f(x) es, pues,

$f (x) = {(x + 1)}^{2} (2 x + 1) (x - 2)$

Si fijamos f(x) = 0 y resolvemos esto, obtenemos que las raíces de f son,

$x = - 1, x = - \frac{1}{2} a n d x = 2$

Determina todos los ceros racionales del polinomio

$f (x) = 2 x^{4} - x^{3} - 15 x^{2} + 8 x + 20$ .

Paso 1: Utilizando el Teorema de los Ceros Racionales, enumeraremos todos los posibles ceros racionales de la forma $\frac{p}{q}$ .

Aquí, p debe ser un factor de $a_{0} = 20$ y q debe ser un factor de $a_{n} = 2$ .

Por tanto, los posibles ceros racionales de f son:

$\pm 1, \pm 2, \pm 4, \pm 5, \pm 10, \pm 20, \pm \frac{1}{2} o r \pm \frac{5}{2}$

Paso 2: Ahora aplicaremos la división sintética como antes. Empezaremos con +1.

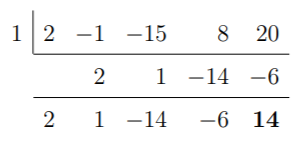
Aquí vemos que +1 da un resto de -14. Por tanto, no es una raíz de f. Probemos con +1. Por tanto, no es una raíz de f. Probemos con -1.

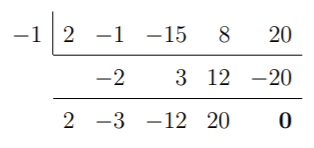
En este caso, -1 da un resto de 0. Por tanto, -1 es una solución de f. El resultado de esta división sintética también nos dice que podemos factorizar f como:

$f (x) = (x + 1) (2 x^{3} - 3 x^{2} - 12 x + 20)$

Paso 3: Ahora, repite este proceso en el cociente

$2 x^{3} - 3 x^{2} - 12 x + 20$

Por el Teorema de los Ceros Racionales, los posibles ceros racionales de este cociente son:

$\pm 1, \pm 2, \pm 4, \pm 5, \pm 10, \pm 20, \pm \frac{1}{2} o r \pm \frac{5}{2}$

Como +1 no es una solución de f, no necesitamos volver a comprobarlo. Sin embargo, debemos aplicar de nuevo la división sintética a -1 para este cociente.

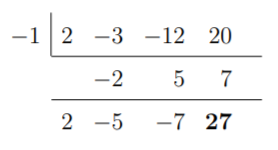
Aquí vemos que -1 da un resto de 27. Por tanto, no es una raíz del cociente. En otras palabras, no hay multiplicidades de la raíz -1. Probemos ahora con +2.

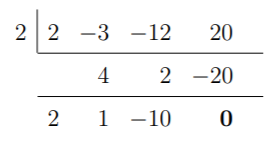
En este caso, +2 da un resto de 0. Así pues, +2 es una solución de f. Por lo tanto, f se factoriza además como:

$f (x) = (x + 1) (x - 2) (2 x^{2} + x - 10)$

Paso 4: Observa que tenemos el cociente

$2 x^{2} + x - 10$

que es efectivamente una ecuación cuadrática que podemos factorizar como:

$(2 x + 5) (x - 2)$

Esto demuestra que las soluciones restantes son:

$x = - \frac{5}{2} a n d x = 2$

La expresión totalmente factorizada de f(x) es, pues,

$f (x) = (x + 1) (x - 2) (2 x + 5) (x - 2)$

Simplificando, tenemos

$f (x) = (x + 1) (2 x + 5) {(x - 2)}^{2}$

Observa que la raíz 2 tiene una multiplicidad de 2. Si establecemos f(x) = 0 y resolvemos esto, obtenemos que las raíces de f son:

$x = - \frac{5}{2}, x = - 1 a n d x = 2$

La geometría y el teorema de los ceros racionales

En este apartado veremos un ejemplo en el que podemos aplicar el Teorema de los Ceros Racionales a un contexto de geometría.

Amy necesita una caja de 24 cm3 de volumen^paraguardar su colección de canicas. Sabe que necesitará una caja con las siguientes características: la anchura es 2 centímetros mayor que la altura, y la longitud es 3 centímetros menor que la altura. A partir de estas características, Amy quiere averiguar las dimensiones reales de este sólido. ¿Cómo resolvería este problema?

Antes de empezar, recordemos la Regla de los Signos de Descartes.

Regla de los signos de Descartes

Sea p un polinomio con coeficientes reales.

El número de ceros reales positivos de p es igual al número de variaciones de signo en p(x) o es menor que éste en un número entero par.
El número de ceros reales negativos de p es igual al número de variaciones de signo de p(-x) o menor que éste en un número entero par.

Volvamos ahora a nuestro ejemplo. La solución se explica a continuación.

Paso 1: Asignar variables

Sean las dimensiones desconocidas del sólido anterior

$h e i g h t = x w i d t h = x + 2 l e n g t h = x - 3$

Esbozando esto, observamos que el bloque tridimensional que necesita Annie debería parecerse al diagrama siguiente.

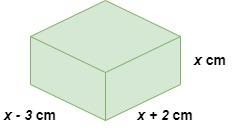
Ejemplo geométrico, Aishah Amri - StudySmarter Originals

Escribiendo la ecuación del volumen y sustituyendo las dimensiones desconocidas anteriores, obtenemos

$h e i g h t \times w i d t h \times l e n g t h = v o l u m e \Rightarrow x (x + 2) (x - 3) = 24$

Expandiendo esto y llevando 24 al lado izquierdo, obtenemos

$x^{3} - x^{2} - 6 x - 24 = 0$

Paso 2: Aplicar el Teorema de los Ceros Racionales

Aquí, el coeficiente principal es 1 y el coeficiente de los términos constantes es 24. Según el Teorema de los Ceros Racionales, los posibles ceros racionales son factores de 24:

$\pm 1, \pm 2, \pm 3, \pm 4, \pm 6, \pm 8, \pm 12 o r \pm 24$

Como la longitud sólo puede ser positiva, sólo consideraremos los ceros positivos, Observando el primer caso de la Regla de los Signos de Descartes, sólo hay un cero real posible. Esto se debe a que sólo hay una variación del signo "+" en el polinomio

$(+) x^{3} - x^{2} - 6 x - 24$

Paso 3: Realizar la división sintética

Utilizando la división sintética, ahora debemos comprobar cada uno de los ceros enumerados anteriormente. Para simplificar, hacemos una tabla para expresar la división sintética para comprobar los posibles ceros reales. La fila de arriba representa los coeficientes del polinomio

$x^{3} - x^{2} - 6 x - 24 = 0$

y la columna del extremo izquierdo representa las raíces probadas. La columna del extremo derecho muestra el resto de la división sintética realizada.

p	1	-1	-6	-24
1	1	0	-6	-30
2	1	1	-4	-32
3	1	2	0	-24
4	1	3	6	0

De esta tabla se deduce que 4 da un resto de 0. Por tanto, 4 es una solución del polinomio

$x^{3} - x^{2} - 6 x - 24 = 0$

Como hemos establecido que sólo hay un cero real positivo, no tenemos que comprobar los demás números.

Paso 4: Evaluar las dimensiones y confirmar los resultados

Así pues, las dimensiones verdaderas son

$h e i g h t = 4 c m w i d t h = 4 - 3 c m = 1 c m l e n g t h = 4 + 2 c m = 6 c m$

Para comprobarlo, observamos que

$4 c m \times 1 c m \times 6 c m = 24 c m^{3}$

que es efectivamente el volumen inicial del sólido rectangular.

Encontrar ceros racionales - Puntos clave

Un cero racional es un número racional escrito como fracción de dos enteros.
El Teorema de los Ceros Racionales afirma que si un polinomio, f(x) tiene coeficientes enteros, entonces cada cero racional de f(x) = 0 puede escribirse de la forma $\frac{p}{q}$ .
El Teorema de los Ceros Racionales sólo nos dice todos los posibles ceros racionales de un polinomio dado.
Identificar los ceros de un polinomio puede ayudarnos a factorizar y resolver un polinomio dado.
Hay 4 pasos para encontrar las soluciones de un polinomio dado:
1. Enumera todos los ceros posibles utilizando el Teorema de los Ceros Racionales.
2. Aplica la división sintética para calcular el polinomio en cada valor de los ceros racionales hallados en el Paso 1.
3. Repite el Paso 1 y el Paso 2 para el cociente obtenido. Detente cuando hayas obtenido un cociente que sea cuadrático (polinomio de grado 2) o que se pueda factorizar fácilmente.
4. Pon todos los factores a cero y resuelve el polinomio.

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Encontrar ceros racionales

¿Qué son los ceros racionales?

Los ceros racionales son las raíces de un polinomio que pueden expresarse como una fracción de dos enteros.

¿Cómo se encuentran los ceros racionales de un polinomio?

Para encontrar los ceros racionales, usa el teorema del factor racional y prueba los posibles ceros en el polinomio.

¿Cuál es el teorema del factor racional?

El teorema del factor racional establece que cualquier cero racional de un polinomio es un factor del término constante dividido por un factor del coeficiente principal.

¿Se puede usar la factorización para encontrar los ceros racionales?

Sí, al factorizar el polinomio en productos de binomios, los ceros racionales pueden determinarse.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 13 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Encontrar ceros racionales

Equipo editorial StudySmarter

Ceros racionales

Teorema de los ceros racionales

Aplicación del Teorema de los Ceros Racionales

Encontrar los posibles ceros racionales de un polinomio

Encontrar los ceros racionales de un polinomio

La geometría y el teorema de los ceros racionales

Regla de los signos de Descartes

Encontrar ceros racionales - Puntos clave

Aprende más rápido con las 0 tarjetas sobre Encontrar ceros racionales

Preguntas frecuentes sobre Encontrar ceros racionales

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Empresa

Nuestros productos

Ponte en contacto

Encontrar ceros racionales

Equipo editorial StudySmarter

Ceros racionales

Teorema de los ceros racionales

Aplicación del Teorema de los Ceros Racionales

Encontrar los posibles ceros racionales de un polinomio

Encontrar los ceros racionales de un polinomio

La geometría y el teorema de los ceros racionales

Regla de los signos de Descartes

Encontrar ceros racionales - Puntos clave

Aprende más rápido con las 0 tarjetas sobre Encontrar ceros racionales

Preguntas frecuentes sobre Encontrar ceros racionales

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Crea una cuenta gratuita para guardar esta explicación.

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.