Funciones inversas: Ejemplos, Explicación

Saltar a un capítulo clave

Sólo las Funciones uno a uno (en las que un valor del dominio va a un único valor del intervalo) pueden tener inversas.

Las funciones uno a uno son aquellas en las que un valor del dominio corresponde a un único valor del intervalo. A diferencia de las funciones uno a muchos, en las que un valor del dominio puede ir a varios valores del intervalo.

Encontrar la inversa de una función

Para hallar la inversa de una función, tienes que

Sustituir la notación de la función por y (por ejemplo, f (x) se convierte en y)
Reordenar la función para que x sea el sujeto
Sustituir la x por la notación de la función inversa (por ejemplo, x se convierte en $f^{- 1} (x)$ e y con x

Encuentra la función inversa de f (x) = 5x + 6

Sustituye la notación de la función por y: y = 5x + 6
Reorganiza la función de modo que x sea el sujeto: $y - 6 = 5 x$ entonces $\frac{(y - 6)}{5} = x$
Sustituye la x por la notación de la función inversa e y por x: $g^{- 1} (x) = \frac{x - 6}{5}$

Encuentra la función inversa de $j (x) = x^{2} - 6$

Sustituye la notación de la función por y: $y = x^{2} - 6$
Reorganiza la función de modo que x sea el sujeto: $y + 6 = x^{2}$ entonces $\sqrt{y + 6} = x$
Sustituye x por la notación de la función inversa e y por x: $j^{- 1} (x) = \sqrt{x + 6}$

Responder a las preguntas sobre funciones inversas

Hay varios tipos de preguntas que te pueden hacer sobre funciones inversas. Las preguntas pueden pedirte que utilices uno o varios métodos.

Resolver la función cuando se conoce x

Este tipo de pregunta se muestra mediante $f^{- 1} (x)$ donde x se sustituye por una constante como , $f^{- 1} (4)$ . Para resolver estas preguntas, se sustituyen todas las x por el Número de la función.

Resolver $f^{- 1} (4) = 6 x - 2$

f^{- 1} (4) = 6 (4) - 2 = 24 - 2 = 22

$f^{- 1} (4) = 22$

Resolver la función cuando se fija en un valor

Este tipo de pregunta se muestra a través de $g^{- 1} (x) = y$ . Para resolver este tipo de pregunta, estableces la función igual a y y luego reordenas la pregunta para obtener x por sí sola.

Cuando $g^{- 1} (x) = 6 x + 4$ encuentra x cuando $g^{- 1} (x) = 58$

$58 = 6 x + 4$

$6 x = 54$

$x = 9$

Trabajar con dominios y rangos

Se te puede pedir que encuentres dominios y rangos de funciones inversas. El dominio (conjunto de valores de entrada) de la función original será el rango (conjunto de posibles valores de salida) de la función inversa. El dominio de la función inversa será el rango de la función original.

dominio

(Conjunto de valores de entrada)

Rango

(Conjunto de posibles valores de salida)

Función original

Función inversa

Función original

Halla la inversa de $h (x) = 3 x^{2} + 4$ con un dominio de $x \geq 5$ . Indica el dominio y el rango de $h^{- 1} (x)$ .

Parte 1) Encontrar la inversa.

$y = 3 x^{2} + 4$
$y - 4 = 3 x^{2}$ entonces $\frac{y - 4}{3} = x^{2}$ entonces $x = \sqrt{\frac{y - 4}{3}}$
$h^{- 1} (x) = \sqrt{\frac{y - 4}{3}}$

Parte 2) Encontrar el dominio y el rango de la inversa Como ya se ha dicho, el dominio de las funciones originales es el rango de la inversa. Por tanto, el rango de

h^{- 1} (x)

x \geq 5

. Para hallar el dominio de

h^{- 1} (x)

puedes hallar el rango de la función original, así que vamos a sustituir el valor por el dominio.

h (5) = 3 (5^{2}) + 4

= 3 (25) + 4

= 79

$x \geq 79$

Rango:

x \geq 5

Dominio:

x \geq 79

Representación gráfica de funciones inversas

Hay dos formas de dibujar una función inversa:

1) Reflejando directamente la función original en la recta y = x utilizando tus habilidades de transformación de una gráfica.

2) Hallando la función inversa y trazando después las coordenadas x e y.

Reflejar directamente la función original en la recta y = x

Una función inversa es la reflexión de la función original en la recta y = x, por tanto podemos utilizar la recta original y la recta y = x como recta de reflexión.

Representa gráficamente la inversa de f (x) = 2x + 4

1) La función original (rojo) representada gráficamente

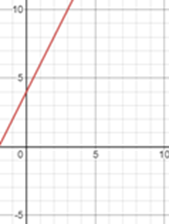
2) La función original (rojo) y la recta de reflexión, y = x (azul)

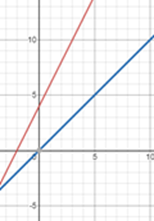
3) La función inversa (verde) se obtiene reflejando la función original (roja) en la recta de reflexión (x = y) (azul).

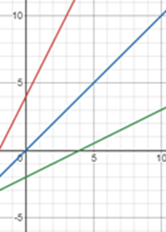
Este método puede ser un poco más difícil cuando la función original tiene una variable elevada a una potencia distinta de 1; por ejemplo, las cuadráticas $(x^{2})$

Trazar las coordenadas de las funciones inversas

Tras hallar la función inversa, puedes trazar el dominio y el rango (es decir, las coordenadas x e y)

Traza la función inversa $g^{- 1} (x) = {(x - 2)}^{2} - 4$ con el dominio $0 \leq x \leq 6$

En primer lugar, halla las coordenadas y utilizando la función inversa y el dominio y, a continuación, introduce los valores en una tabla.
x 0 1 2 3 $4$ 5 $6$
y 0 -3 -4 -3 0 5 $12$
A continuación, traza las coordenadas en la gráfica

Pie de foto

A continuación, dibuja la función inversa trazando una recta que pase por todos los puntos y se extienda a través de ellos.

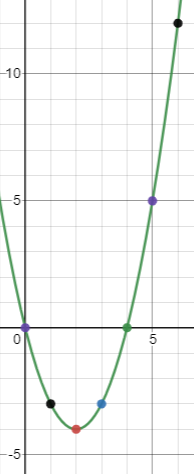
Funciones inversas - Puntos clave

Las funciones inversas son lo contrario de la función original. Su notación difiere de la de las funciones normales debido a la $^{- 1}$ . Sólo las funciones uno a uno pueden tener funciones inversas.
Las funciones inversas pueden formarse 1) sustituyendo la notación de la función por y; 2) reordenando la función original para que x sea el sujeto; 3) sustituyendo x por la notación de la función inversa e y por x.
Cuando se forma la función inversa, el dominio es el rango de la función original y el rango es el dominio de la función original.

Aprende con 0 tarjetas de Funciones inversas en la aplicación StudySmarter gratis

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Funciones inversas

¿Qué es una función inversa?

Una función inversa es aquella que deshace la operación de la función original. Si f(x) lleva x a y, la inversa f⁻¹(y) lleva y de vuelta a x.

¿Cómo encontrar la función inversa de una función?

Para encontrar la inversa, intercambia x e y en la ecuación y luego despeja y. La nueva ecuación es f⁻¹(x).

¿Cuándo una función tiene una inversa?

Una función tiene una inversa si es biyectiva, es decir, es inyectiva (ningún valor de salida se repite) y sobreyectiva (cubre todos los valores de salida posibles).

¿Cuál es el propósito de las funciones inversas?

Las funciones inversas se utilizan para deshacer operaciones y resolver ecuaciones donde necesitamos revertir el proceso original de la función.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 6 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Funciones inversas

Equipo editorial StudySmarter

Encontrar la inversa de una función