La Fórmula Cuadrática y el Discriminante: Método, Ejemplos

Q: ¿Qué es la fórmula cuadrática?

La fórmula cuadrática es una herramienta matemática que soluciona ecuaciones cuadráticas y es: x = [-b ± √(b²-4ac)] / 2a.

Q: ¿Qué es el discriminante en una ecuación cuadrática?

El discriminante es la parte de la fórmula cuadrática b²-4ac y determina la cantidad y el tipo de soluciones de la ecuación.

Q: ¿Cómo se interpreta el valor del discriminante?

El discriminante indica: si es positivo, hay dos soluciones reales; si es cero, hay una solución real; si es negativo, no hay soluciones reales.

Q: ¿Para qué se usa la fórmula cuadrática?

La fórmula cuadrática se usa para encontrar las soluciones de ecuaciones cuadráticas de la forma ax² + bx + c = 0.

Saltar a un capítulo clave

Aunque algunos de estos métodos parecen ser la mejor opción para resolver cualquier tipo de ecuación cuadrática, pueden resultar bastante difíciles si en la ecuación cuadrática dada intervienen fracciones o decimales. Sin embargo, ¡no temas! Resulta que existe una solución para resolver cualquier forma de ecuación cuadrática expresada como la definición anterior. Se conoce como Fórmula Cuadrática.

La Fórmula Cuadrática es una herramienta importante que se utiliza para determinar las soluciones de cualquier ecuación cuadrática dada. Podemos aplicar este concepto al resolver ecuaciones cuadráticas que no pueden factorizarse mediante métodos de factorización estándar.

Ten en cuenta que, de hecho, podemos utilizar la Fórmula Cuadrática para hallar las soluciones de cualquier forma de ecuación cuadrática, incluso de las que se pueden factorizar.

La fórmula cuadrática

Antes de sumergirnos en este tema, recordemos primero la forma estándar de una ecuación cuadrática.

La forma estándar de una ecuación cuadrática es $a x^{2} + b x + c = 0,$ donde $a \neq 0 .$

Teniendo esto en cuenta, introduzcamos ahora la Fórmula Cuadrática.

Para una ecuación cuadrática de la forma donde las soluciones vienen dadas por la Fórmula Cuadrática,

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

Observa que la Fórmula Cuadrática tiene el signo"± ". Esto significa que la fórmula produce dos soluciones, a saber

$x = \frac{- b - \sqrt{b^{2} - 4 a c}}{2 a} a n d x = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}$ .

Dado que la Fórmula Cuadrática nos indica las raíces de una ecuación cuadrática dada, podemos localizar fácilmente estos puntos y trazar la gráfica con mayor precisión.

Derivación de la fórmula cuadrática

La fórmula cuadrática se obtiene completando el cuadrado. En esta sección se explica su derivación paso a paso, como se indica a continuación.

Dada la forma general de una ecuación cuadrática $a x^{2} + b x + c = 0$ :

Paso 1: Divide la expresión por a

$x^{2} + \frac{b}{a} x + \frac{c}{a} = 0$

Paso 2 : Resta $\frac{c}{a}$ de cada lado

$x^{2} + \frac{b}{a} x = - \frac{c}{a}$

Paso3 : Completa el cuadrado

$x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} = - \frac{c}{a} + {(\frac{b}{2 a})}^{2} \Rightarrow x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} = - \frac{c}{a} + \frac{b^{2}}{4 a^{2}}$

Paso4 : Factoriza el lado izquierdo y simplifica el lado derecho

${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$

Paso5 : Raíz cuadrada de cada lado

¡No olvides el signo "±"!

$x + \frac{b}{2 a} = \pm \sqrt{\frac{b^{2} - 4 a c}{4 a^{2}}} \Rightarrow x + \frac{b}{2 a} = \pm \frac{\sqrt{b^{2} - 4 a c}}{2 a}$

Paso 6: Resta $\frac{b}{2 a}$ a cada lado

$x = \pm \frac{\sqrt{b^{2} - 4 a c}}{2 a} - \frac{b}{2 a}$

Paso 7: Simplifica la expresión

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Nota: este método de completar el cuadrado se explica detalladamente en el tema Completar los cuadrados. Este tema contiene ejemplos claramente trabajados que muestran cómo se aplica esta derivación a una ecuación cuadrática dada. Échale un vistazo si quieres profundizar en este tema.

El discriminante

En los siguientes apartados, veremos las propiedades de las raíces para ecuaciones cuadráticas dadas. Conoceremos un nuevo concepto llamado discriminante. El discriminante desempeña un papel crucial en la comprensión de la naturaleza de las raíces de una ecuación cuadrática.

Antes de examinar la idea de discriminante, debemos familiarizarnos con varios términos importantes que nos ayudarán a comprender mejor este tema. Empecemos por definir una raíz racional y una irracional.

Una raíz racional es una solución que puede expresarse como cociente de dos números enteros.

Se representan de la forma $\frac{p}{q}$ donde p y q son números enteros en los que p es la constante del polinomio y q es el coeficiente principal.

Una raíz irracional es una solución que no puede expresarse como cociente de dos enteros. A menudo se representan mediante decimales infinitos no repetidos o surds.

A continuación, definiremos lo que significa ser un cuadrado perfecto. Este concepto es crucial cuando empecemos a utilizar la Fórmula Cuadrática, ya que determina si las raíces de nuestra ecuación cuadrática dada son racionales o irracionales, ¡como pronto veremos!

Un cuadrado perfecto es un número entero que es el cuadrado de un número entero, es decir, el producto de algún número entero por sí mismo. Tiene la forma $p \times p = p^{2}$ donde p es un número entero. Esencialmente, $\sqrt{p^{2}} = p$ .

Algunos ejemplos son 9 (³²), 16 (⁴²), 25 (⁵²), etc.

Ahora que ya tenemos ordenadas las definiciones clave, pasemos al concepto de discriminante y su relación con las propiedades de las raíces.

El discriminante y las propiedades de las raíces

Para hallar el número de raíces de una ecuación cuadrática dada, utilizaremos el discriminante. También podemos determinar el tipo de raíces que tiene la expresión.

El discriminante de un polinomio cuadrático sirve para hallar el número y tipo de soluciones que tiene una ecuación cuadrática. Se describe mediante la fórmula

$D = b^{2} - 4 a c .$

Observa que se trata de la componente dentro de la raíz cuadrada en la Fórmula Cuadrática.

La condición de un discriminante tiene tres casos.

Caso 1: D > 0

Cuando el determinante es mayor que cero, o dicho de otro modo, b2^-4ac > 0, obtenemos dos raíces reales distintas. Esto se puede clasificar como sigue.

Si b2 ^- 4ac es un cuadrado perfecto, tenemos dos raíces racionales reales;
Si b2 ^- 4ac no es un cuadrado perfecto, tenemos dos raíces irracionales reales.

A continuación se muestra la gráfica de este caso.

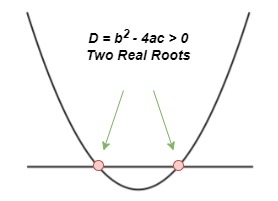
Discriminant case when D > 0, StudySmarter Originals

Caso discriminante cuando D > 0, StudySmarter Originals

Caso 2: D = 0

Cuando el determinante es igual a cero, o lo que es lo mismo, b2^- 4ac = 0, obtenemos una raíz real. Esto también se conoce como raíz repetida. La gráfica de este caso se muestra a continuación.

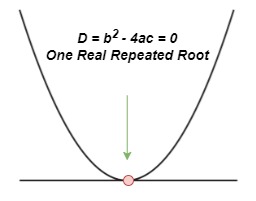
Caso discriminante cuando D = 0, StudySmarter Originals

Caso del determinante cuando D = 0, StudySmarter Originals

Caso 3: D < 0

Cuando el determinante es menor que cero, o dicho de otro modo, b2^-4ac < 0, obtenemos dos raíces complejas conjugadas. Esto significa que nuestra solución es de la forma a + bi, donde a es la parte real y b es la parte imaginaria. A continuación se muestra la gráfica de este caso.

Discriminant case when D < 0, StudySmarter Originals Caso discriminante cuando D < 0, StudySmarter Originals

Recuerda que la unidad imaginaria es $i = \sqrt{- 1} o r i^{2} = - 1$

Utilizar la fórmula cuadrática y el discriminante para hallar raíces

En este apartado veremos algunos ejemplos trabajados que demuestran la aplicación de la Fórmula Cuadrática y el discriminante para buscar soluciones a una ecuación cuadrática dada.

Dos raíces racionales reales

Resuelve la siguiente ecuación cuadrática.

$x^{2} - 12 x - 28 = 0$

Calcula el discriminante e identifica el número y tipo de raíces que tiene esta expresión. Después, utiliza la Fórmula Cuadrática para evaluar sus soluciones.

Solución

Paso1: Identifica a, b y c

a = 1, b = - 12 a n d c = - 28

Paso2: Calcula el discriminante

$D = b^{2} - 4 a c = {(- 12)}^{2} - 4 (1) (- 28) \Rightarrow D = 144 + 112 \Rightarrow D = 256$

Como D > 0, hay dos raíces reales distintas.

Paso3: Hallar las soluciones

Utilizando la Fórmula Cuadrática obtenemos

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} = \frac{- (- 12) \pm \sqrt{256}}{2 (1)}$

Observa que la componente dentro de la raíz cuadrada es D, o lo que es lo mismo $\sqrt{b^{2} - 4 a c} = \sqrt{D}$

$\Rightarrow x = \frac{12 \pm 16}{2}$

Aquí $b^{2} - 4 a c = D = 256$ es un cuadrado perfecto, por lo que obtenemos un par de raíces racionales

$x = \frac{12 - 16}{2} = \frac{- 4}{2} = - 2 a n d x = \frac{12 + 16}{2} = \frac{28}{2} = 14$

Por tanto, las soluciones son $x = - 2 a n d x = 14$ .

A continuación se representa la gráfica de esta ecuación cuadrática. Los puntos verdes representan las soluciones de la expresión.

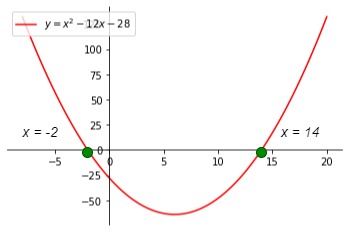
Ejemplo 1, Originales de StudySmarter

Ejemplo 1, StudySmarter Originals

Dos Raíces Irracionales Reales

Resuelve la siguiente ecuación cuadrática.

$2 x^{2} + 4 x - 5 = 0$

Calcula el discriminante e identifica el número y tipo de raíces que tiene esta expresión. Después, utiliza la Fórmula Cuadrática para evaluar sus soluciones.

Solución

Paso1: Identifica a, b y c

a = 2, b = 4 a n d c = - 5

Paso2: Calcula el discriminante

$D = {(4)}^{2} - 4 (2) (- 5) \Rightarrow D = 16 + 40 \Rightarrow D = 56$

Como D > 0, hay dos raíces reales distintas.

Paso3: Hallar las soluciones

Utilizando la Fórmula Cuadrática obtenemos

$x = \frac{- (4) \pm \sqrt{56}}{2 (2)} \Rightarrow x = \frac{- 4 \pm 2 \sqrt{14}}{4}$

Aquí $b^{2} - 4 a c = D = 56$ no es un cuadrado perfecto, por lo que obtenemos un par de raíces irracionales

$x = \frac{- 4 - 2 \sqrt{14}}{4} = - 1 - \frac{\sqrt{14}}{2} = - 2.87 (c o r r e c t t o t w o d e c i m a l p l a c e s) a n d x = \frac{- 4 + 2 \sqrt{14}}{4} = - 1 + \frac{\sqrt{14}}{2} = 0.87 (c o r r e c t t o t w o d e c i m a l p l a c e s)$

Por tanto, las soluciones son $x = - 2.87 a n d x = 0.87$ .

A continuación se representa la gráfica de esta ecuación cuadrática. Los puntos verdes representan las soluciones de la expresión.

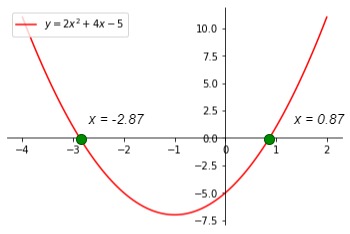
Ejemplo 2, Originales de StudySmarter

Ejemplo 2, StudySmarter Originals

Observa que puedes mantener las raíces en la forma exacta y que los decimales son una respuesta aproximada.

Una raíz real repetida

Resuelve la siguiente ecuación cuadrática.

$x^{2} + 22 x + 121 = 0$

Calcula el discriminante e identifica el número y tipo de raíces que tiene esta expresión. Después, utiliza la Fórmula Cuadrática para evaluar sus soluciones.

Solución

Paso1: Identifica a, b y c

a = 1, b = 22 a n d c = 121

Paso 2: Calcula el discriminante

$D = {(22)}^{2} - 4 (1) (121) \Rightarrow D = 484 - 484 \Rightarrow D = 0$

Como D = 0, hay una raíz real distinta.

Paso3: Hallar las soluciones

Utilizando la Fórmula Cuadrática obtenemos

$x = \frac{- (22) \pm \sqrt{0}}{2 (1)}$

Observando que $\sqrt{0} = 0$

$\Rightarrow x = \frac{- 22}{2} \Rightarrow x = - 11$

Por tanto, la solución es $x = - 11$ .

A continuación se representa la gráfica de esta ecuación cuadrática. Los puntos verdes representan las soluciones de la expresión.

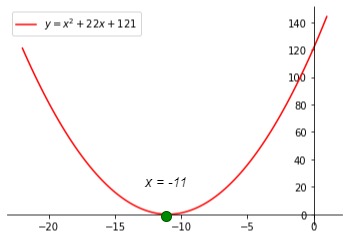
Ejemplo 3, Originales de StudySmarter

Ejemplo 3, StudySmarter Originals

Dos raíces complejas

Resuelve la siguiente ecuación cuadrática.

$x^{2} - 4 x + 13 = 0$

Calcula el discriminante e identifica el número y tipo de raíces que tiene esta expresión. Después, utiliza la Fórmula Cuadrática para evaluar sus soluciones.

Solución

Paso1: Identifica a, b y c

$a = 1, b = - 4 a n d c = 13$

Paso2: Calcula el discriminante

$D = {(- 4)}^{2} - 4 (1) (13) \Rightarrow D = 16 - 52 \Rightarrow D = - 36$

Como D < 0, hay dos raíces complejas conjugadas.

Paso3: Hallar las soluciones

Utilizando la Fórmula Cuadrática obtenemos

$x = \frac{- (- 4) \pm \sqrt{- 36}}{2 (1)}$

Observando que $\sqrt{- 1} = i$

$\Rightarrow x = \frac{4 \pm i \sqrt{36}}{2} \Rightarrow x = \frac{4 \pm 6 i}{2}$

Simplificando, obtenemos

$\Rightarrow x = 2 \pm 3 i$

Por tanto, las soluciones son $x = 2 - 3 i a n d x = 2 + 3 i$ .

A continuación se representa la gráfica de esta ecuación cuadrática. Los puntos verdes representan las soluciones de la expresión.

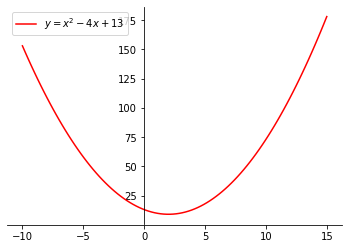
Ejemplo 4, Originales de StudySmarter

Ejemplo 4, StudySmarter Originals

Observa que en esta gráfica no hay soluciones marcadas. Esto se debe a que las soluciones son imaginarias y no pueden representarse en el plano cartesiano estándar. El plano cartesiano se representa con números reales, ¡no con números imaginarios! En este caso, podemos "suponer" la forma de la gráfica basándonos en el coeficiente del término ^x2 y en que la intersección y viene dada por la ecuación cuadrática inicial.

Discriminante de una ecuación cúbica

En este apartado estudiaremos el discriminante de una ecuación cúbica e identificaremos los tipos de raíces que tiene la expresión, dado el valor de su discriminante.

Para una ecuación cúbica de la forma (general)

$a x^{3} + b x^{2} + c x + d = 0$ ,

donde a ≠ 0, el discriminante se describe mediante la fórmula

$D = 18 a b c d + b^{2} c^{2} - 4 b^{3} d - 4 a c^{3} - 27 a^{2} d^{2}$ .

La fórmula para evaluar el discriminante de las ecuaciones cúbicas puede ser bastante larga. Las preguntas en las que se puede aplicar esta fórmula suelen ser poco frecuentes en este temario. Sin embargo, puede ser útil saber cómo se hace para mayor claridad.

Al igual que en el caso cuadrático, el discriminante de las ecuaciones cúbicas tiene tres condiciones.

Caso 1: D > 0

Cuando el discriminante es mayor que cero, obtenemos tres raíces reales (distintas).

Digamos que tenemos la ecuación cúbica $x^{3} - 6 x^{2} + 11 x - 6 = 0$ .

Aquí, el discriminante es $D = 4 > 0$ .

Por tanto, tenemos tres raíces reales distintas. Factorizando esta expresión obtenemos

$(x - 1) (x - 2) (x - 3) = 0$

Por tanto, las raíces son $x = 1, x = 2 a n d x = 3$ .

La gráfica se muestra a continuación.

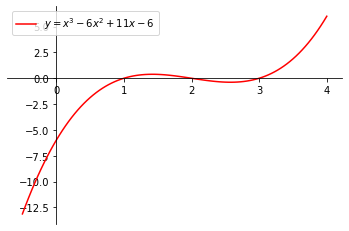
Ejemplo 5, Originales de StudySmarter

Ejemplo 5, StudySmarter Originals

Caso 2: D = 0

Caso 2(a): Si el discriminante es igual a cero y ^b2 = 3ac, obtenemos tres raíces reales repetidas (raíz triple distinta).

Digamos que tenemos la ecuación cúbica $x^{3} - 3 x^{2} + 3 x - 1 = 0$ .

Aquí, el discriminante es $D = 0$ .

Además , ${(- 3)}^{2} = 9 = 3 (1) (3) = 9$ .

Por tanto, tenemos tres raíces reales repetidas. Factorizando esta expresión se obtiene

${(x - 1)}^{3} = 0$

Por tanto, las raíces son $x = 1$ .

La gráfica se muestra a continuación.

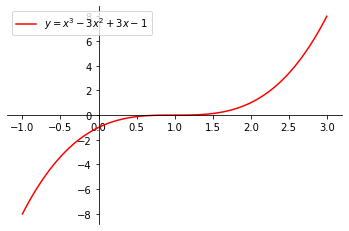
Ejemplo 6, Originales de StudySmarter

Ejemplo 6, StudySmarter Originals

Caso 2(b): Si el discriminante es igual a cero y ^b2 ≠ 3ac, obtenemos dos raíces reales repetidas (raíz doble distinta) y una raíz real (distinta).

Digamos que tenemos la ecuación cúbica $x^{3} - 4 x^{2} + 5 x - 2 = 0$ .

Aquí, el discriminante es $D = 0$ .

Además , ${(- 4)}^{2} = 16 \neq 3 (1) (5) = 15$ .

Por tanto, tenemos dos raíces reales repetidas y una raíz real. Factorizando esta expresión se obtiene

${(x - 1)}^{2} (x - 2) = 0$

Por tanto, las raíces son $x = 1 a n d x = 2$ .

La gráfica se muestra a continuación.

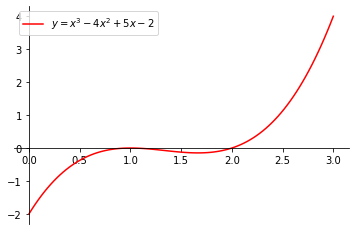
Ejemplo 7, Originales de StudySmarter

Ejemplo 7, StudySmarter Originals

Caso 3: D < 0

Cuando el discriminante es menor que cero, obtenemos una raíz real (distinta) y un par de raíces complejas conjugadas.

Digamos que tenemos la ecuación cúbica $x^{3} - x^{2} + 16 x - 16 = 0$ .

Aquí, el discriminante es $D = - 18496 < 0$ .

Por tanto, tenemos una raíz real y dos raíces complejas conjugadas. Factorizando esta expresión obtenemos

$(x - 1) (x^{2} + 16) = 0$

Por tanto, las raíces son $x = 1, x = 4 i a n d x = - 4 i$ .

La gráfica se muestra a continuación.

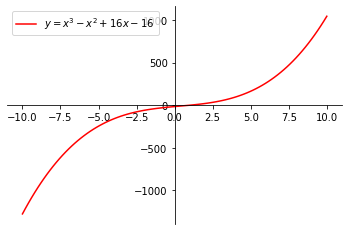
Ejemplo 8, Originales de StudySmarter

Ejemplo 8, StudySmarter Originals

La fórmula cuadrática y el discriminante - Puntos clave

La Fórmula Cuadrática se utiliza para determinar las soluciones de una ecuación cuadrática dada.
Para una ecuación cuadrática de la forma $a x^{2} + b x + c = 0,$ la fórmula cuadrática de es $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$
El Discriminante se utiliza para hallar el número y tipo de soluciones que tiene una ecuación cuadrática. Viene dado por la fórmula D = ^b2 - 4ac.
Las condiciones del discriminante se resumen en la tabla siguiente.

Valor del discriminante	Tipo y número de raíces	Gráfica
D > 0, D es un cuadrado perfecto	2 Raíces racionales reales	Gráfica cuando D > 0, Aishah Amri - StudySmarter Originals
D > 0, D no es un cuadrado perfecto	2 Raíces reales irracionales	Gráfica cuando D > 0, Aishah Amri - StudySmarter Originals
D = 0	1 Raíz Real Repetida	Gráfica cuando D = 0, Aishah Amri, StudySmarter Originals
D < 0	2 Raíces complejas conjugadas	Gráfico cuando D = 0, Aishah Amri, StudySmarter Originals

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre La Fórmula Cuadrática y el Discriminante

¿Qué es la fórmula cuadrática?

La fórmula cuadrática es una herramienta matemática que soluciona ecuaciones cuadráticas y es: x = [-b ± √(b²-4ac)] / 2a.

¿Qué es el discriminante en una ecuación cuadrática?

El discriminante es la parte de la fórmula cuadrática b²-4ac y determina la cantidad y el tipo de soluciones de la ecuación.

¿Cómo se interpreta el valor del discriminante?

El discriminante indica: si es positivo, hay dos soluciones reales; si es cero, hay una solución real; si es negativo, no hay soluciones reales.

¿Para qué se usa la fórmula cuadrática?

La fórmula cuadrática se usa para encontrar las soluciones de ecuaciones cuadráticas de la forma ax² + bx + c = 0.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 14 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

La Fórmula Cuadrática y el Discriminante

Equipo editorial StudySmarter

La fórmula cuadrática

Derivación de la fórmula cuadrática

El discriminante

El discriminante y las propiedades de las raíces

Caso 1: D > 0

Caso 2: D = 0

Caso 3: D < 0

Utilizar la fórmula cuadrática y el discriminante para hallar raíces

Dos raíces racionales reales

Dos Raíces Irracionales Reales

Una raíz real repetida

Dos raíces complejas

Discriminante de una ecuación cúbica

Caso 1: D > 0

Caso 2: D = 0

Caso 3: D < 0

La fórmula cuadrática y el discriminante - Puntos clave

Aprende más rápido con las 0 tarjetas sobre La Fórmula Cuadrática y el Discriminante

Preguntas frecuentes sobre La Fórmula Cuadrática y el Discriminante

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Empresa

Nuestros productos

Ponte en contacto

La Fórmula Cuadrática y el Discriminante

Equipo editorial StudySmarter

La fórmula cuadrática

Derivación de la fórmula cuadrática

El discriminante

El discriminante y las propiedades de las raíces

Caso 1: D > 0

Caso 2: D = 0

Caso 3: D < 0

Utilizar la fórmula cuadrática y el discriminante para hallar raíces

Dos raíces racionales reales

Dos Raíces Irracionales Reales

Una raíz real repetida

Dos raíces complejas

Discriminante de una ecuación cúbica

Caso 1: D > 0

Caso 2: D = 0

Caso 3: D < 0

La fórmula cuadrática y el discriminante - Puntos clave

Aprende más rápido con las 0 tarjetas sobre La Fórmula Cuadrática y el Discriminante

Preguntas frecuentes sobre La Fórmula Cuadrática y el Discriminante

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Acerca de StudySmarter

Equipo editorial StudySmarter

Guardar explicación

Crea una cuenta gratuita para guardar esta explicación.

Únete a más de 22 millones de estudiantes que aprenden con nuestra app StudySmarter.