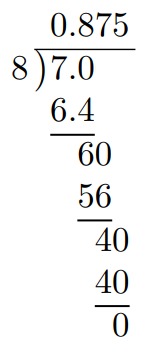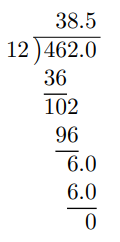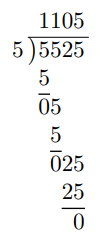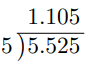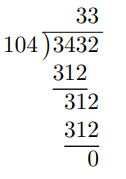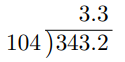
Ejemplo 1, Aishah Amri - StudySmarter Originals
A primera vista, sin duda podríamos representar este número como una fracción. Como hemos visto en artículos anteriores, las fracciones expresan números que no son enteros. En este caso, tendríamos la fracción . ¿Y si te dijera que hay otra forma de escribir números que no son enteros? Pues sí. Se llaman decimales.
En este artículo vamos a explorar los decimales, su definición, las operaciones con decimales, las operaciones mixtas y muchos ejemplos.
Decimales
Empecemos por la definición de decimal.
Un decimal es un número que contiene una coma.
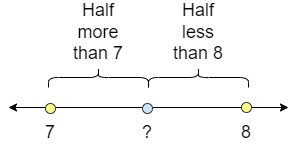
La coma decimal se representa mediante un punto y separa un número entero de su parte fraccionaria. El valor de la parte fraccionaria es siempre menor que uno. El número de cifras formadas por la parte fraccionaria determina el número de decimales. Demostremos la posición de los decimales en una recta numérica para tener una idea más clara de este concepto. Se muestra a continuación.
Ejemplo 2, Aishah Amri - StudySmarter Originals
Otra forma de ver los decimales es representándolos en una tabla de valor posicional. Esto nos ayudará a identificar el número de posiciones decimales para cada valor decimal dado, lo que es importante tener en cuenta al realizar operaciones con decimales. Construyamos esta tabla de valor posicional a continuación.
| Miles | Centenas | Decenas | Unos | Punto decimal (.) | Décimas | Centésimas | Milésimas | |
| 1000 | 100 | 10 | 1 | . | 0.1 | 0.01 | 0.001 | |
Los dígitos antes del punto decimal representan la parte entera del número, mientras que los dígitos después del punto decimal representan la parte decimal del número.
Dado el decimal 12,45, la posición de cada número se define a continuación.
| Dígito | 1 | 2 | . | 4 | 5 |
| Valor posicional | Decenas | Unos | Decimal | Décimas | Centésimas |
| El número asociado al valor posicional | 10 | 2 | . | 0.4 | 0.05 |
En algunos libros de texto, la parte fraccionaria también se denomina parte decimal.
El número decimal 3,4512 tiene 3 como componente de número entero y 0,4512 como parte fraccionaria.
Aquí hay cuatro decimales, ya que hay cuatro dígitos después de la coma.
Recapitula: Conversión de fracciones a decimales
Método 1: Con una calculadora
La forma más sencilla de convertir una fracción en decimal es utilizando una calculadora. Simplemente divide el numerador por el denominador. Si introduces estos dígitos en la calculadora, obtendrás la respuesta.
Método 2: División larga
Utiliza la división larga para convertir en un decimal.
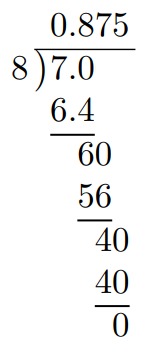
Por tanto,
Recapitula: Conversión de porcentajes a decimales
Recuerda que un porcentaje tiene la forma . Para convertir un porcentaje en decimal, basta con eliminar el signo % y dividir el dígito restante por 100. Esto se hace moviendo el punto decimal dos espacios a la izquierda.
Convertir el 45% en un decimal.
Desplazando dos espacios a la izquierda, obtenemos 45% = 0,45
Convierte el 3,67% en un decimal.
Desplazando dos espacios a la izquierda del punto decimal, obtenemos 3,67% = 0,0367
Orden de las operaciones
Al realizar operaciones aritméticas básicas con decimales, como sumas, restas, multiplicaciones y divisiones, debemos tener en cuenta el orden de las operaciones. Esto es especialmente importante cuando se trata de operaciones mixtas con decimales. El orden de las operaciones con decimales se abrevia con las siglas PEMDAS, que se describen en la tabla siguiente.
| Encargar | Carta | Concepto | Explicación |
| 1 | P | Paréntesis | Son expresiones dentro de un par de paréntesis o corchetes como (x + y) y [x + y] o en forma de agrupación como |
| 2 | E | Exponente | Son expresiones de la forma xy |
| 3 | M | Multiplicación | Estas dos operaciones tienen la misma precedencia, por lo que simplemente ejecutamos el orden de operación de izquierda a derecha |
| 4 | D | División | |
| 5 | A | Suma | Estas dos operaciones tienen la misma precedencia, por lo que simplemente ejecutamos el orden de operación de izquierda a derecha |
| 6 | S | Resta |
Recuerda siempre PEMDAS: Paréntesis, Exponente, Multiplicación/División, Suma/Resta.
Suma y resta de decimales
La suma y resta de decimales es similar a la suma y resta de enteros. Siempre empezamos por la derecha y aplicamos el método de la columna. El método de la columna ayuda a mantener claramente los valores de posición y los decimales para conseguir una suma o resta exacta entre decimales.
Escribe los números en forma de columna de modo que sus decimales queden alineados verticalmente;
Pon ceros como marcadores de posición (si es necesario) para que los números tengan la misma longitud;
Suma o resta utilizando la suma en columna o la resta en columna;
Vuelve a colocar el punto decimal en la suma o diferencia de forma que quede alineado verticalmente con los números que se suman o restan.
Vamos a demostrar este método con algunos ejemplos prácticos.
¡No olvides añadir el punto decimal al final de tu respuesta!
Suma 5,7 y 8,9
Resta 2,3 de 4,8
Suma y resta de decimales con números enteros
Recuerda añadir ceros como marcadores de posición para que los números tengan la misma longitud. A continuación encontrarás algunos ejemplos prácticos que lo demuestran.
Suma 6 y 4,3
Restar 5 a 9.2
Suma y resta de dos decimales distintos
Como antes, asegúrate de que los decimales tienen la misma longitud añadiendo ceros como marcadores de posición. Aquí tienes dos ejemplos prácticos que lo demuestran.
Suma 5,43 y 6,678
Resta 2,3456 de 4,1
Multiplicar decimales
Para multiplicar decimales, debemos tener en cuenta las reglas de multiplicación de decimales.
Elimina el punto decimal de los números dados y realiza la multiplicación como de costumbre;
Cuenta el número de decimales de cada uno de los números originales y halla su suma;
El valor posicional de la respuesta final es la suma de los decimales hallados en el Paso 2;
Coloca el punto decimal en el producto calculado en el Paso 1.
Demostremos esta técnica con los siguientes ejemplos prácticos.
Multiplicar 3,6 por 2,3
Ignorando los decimales, obtenemos 36 × 23 = 826.
Ambos decimales, 3,6 y 2,3 tienen un decimal cada uno.
La suma de estos decimales es dos.
Por tanto, el producto de 36 × 23 = 826 debe tener dos decimales.
Colocando la coma decimal, obtenemos 3,6 × 2,3 = 8,26.
Multiplicación de decimales por números enteros
Multiplica 5,7 por 8
Ignorando los decimales, obtenemos 57 × 8 = 456.
El decimal 5,7 tiene un decimal, mientras que el número entero 8 no tiene decimales.
La suma de estos decimales es uno.
Por tanto, el producto de 57 × 8 = 456 debe tener un decimal.
Colocando la coma decimal, obtenemos 5,7 × 8 = 45,6.
Multiplicación de dos decimales distintos
Multiplica 2,165 por 9,1
Ignorando los decimales, obtenemos 2165 × 91 = 197015.
Los decimales 2,165 y 9,1 tienen 3 cifras decimales y una cifra decimal respectivamente.
La suma de estos decimales es 4.
Por tanto, el producto de 2165 × 91 = 197015 debe tener cuatro decimales.
Colocando la coma decimal, obtenemos 2,165 × 9,1 = 19,7015.
Multiplicación de decimales por potencias de 10
Al multiplicar decimales por potencias de 10, simplemente desplazamos el punto decimal hacia la derecha en función del número de ceros presentes en la potencia de 10. A continuación se muestran dos ejemplos prácticos.
Multiplica 3,87 por 100
Hay dos ceros en el número 100, por lo que debemos desplazar la coma decimal de 3,87 dos posiciones a la derecha.
3.87 × 100 = 387
Multiplica 7,3956 por 1000
Hay tres ceros en el número 1000, por lo que debemos desplazar la coma decimal de 7,3956 tres posiciones a la derecha.
7.3956 × 1000 = 7395.6
Dividir decimales
Al dividir números en general, siempre es más fácil dividir por un número entero.
El divisor es el número por el que dividimos. Por ejemplo, en la expresión 32 ÷ 2,3, 32 es el dividendo y 2,3 es el divisor.
A continuación se indican los pasos esenciales para dividir decimales.
Convierte el divisor en un número entero multiplicándolo por una potencia de 10;
Multiplica el dividendo por la misma potencia de 10 hallada en el paso 1;
Divide estos números utilizando la división larga.
Los siguientes ejemplos prácticos muestran la aplicación de este método.
La respuesta del Paso 3 nos da el mismo rendimiento que si hubiéramos dividido los decimales.
Divide 4,62 entre 0,12
Aquí tenemos 4,62 ÷ 0,12, donde el dividendo es 4,62 y el divisor es 0,12.
Para convertir el divisor en un número entero, lo multiplicamos por 100. El resultado es 0,12 × 100 = 12.
Multiplicando este mismo valor por el dividendo, obtenemos 4,62 × 100 = 462.
Así, tenemos 462 ÷ 12 que es lo mismo que 4,62 ÷ 0,12.
Realizando la división larga, obtenemos
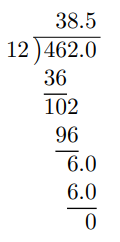
Por tanto, 4,62 ÷ 0,12 = 38,5.
División de decimales con números enteros
Divide 5,525 entre 5
Aquí tenemos 5,525 ÷ 5, donde el dividendo es 5,525 y el divisor es 5.
El divisor ya tiene forma de número entero. Sin embargo, el dividendo sigue teniendo forma decimal.
Para resolver este problema, realizaremos la división larga ignorando el punto decimal del dividendo.
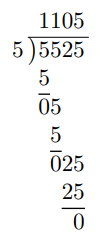
Colocaremos el punto decimal de la respuesta justo encima del punto decimal del dividendo, como se indica a continuación.
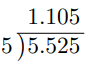
Así, 5,525 ÷ 5 = 1,105.
División de dos decimales distintos
Divide 3,432 entre 1,04
Aquí tenemos 3,432 ÷ 1,04, donde el dividendo es 3,432 y el divisor es 1,04.
Para convertir el divisor en un número entero, lo multiplicamos por 100. El resultado es 1,04 × 100 = 104.
Multiplicando este mismo valor por el dividendo, obtenemos 3,432 × 100 = 343,2.
Por tanto, tenemos 343,2 ÷ 104, que es lo mismo que 3,432 ÷ 1,04.
Aunque el divisor ya está en forma de número entero, el dividendo sigue estando en forma de decimal.
Como antes, realizaremos la división larga ignorando el punto decimal del dividendo.
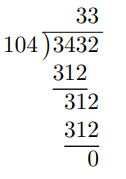
Ahora colocaremos el punto decimal de la respuesta justo encima del punto decimal del dividendo, como se indica a continuación.
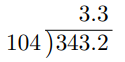
Así, 3,432 ÷ 1,04 = 3,3.
División de decimales por potencias de 10
Cuando dividimos decimales por potencias de 10, simplemente desplazamos el punto decimal hacia la izquierda en función del número de ceros presentes en la potencia de 10. A continuación se muestran dos ejemplos prácticos.
Divide 2,34 entre 10
Hay un cero en el número 10, por lo que debemos desplazar el punto decimal de 2,34 un lugar a la izquierda.
2.34 ÷ 10 = 0.234.
Divide 17635,6 entre 1000
Hay tres ceros en el número 1000, así que debemos desplazar el punto decimal de 17635,6 tres posiciones a la izquierda.
17635.6 ÷ 1000 = 17.6356
Operaciones mixtas con decimales
En este apartado, utilizaremos el orden de operaciones PEMDAS para decimales. A continuación encontrarás algunos ejemplos trabajados.
Evalúa.
Solución
Empezamos convirtiendo el término porcentual
4.5% = 4.5 ÷ 100 = 0.045
Ahora podemos realizar la resta como de costumbre
Así, la respuesta final es 0,078
Evalúa .
Solución
Empezamos convirtiendo el término de la fracción
Ahora podemos sumar como de costumbre
Así, la respuesta final es 1,32
Evalúa.
Solución
Primero calcularemos la expresión dentro del paréntesis
A continuación, realizaremos la multiplicación
Por último, realizaremos la resta
Así, la respuesta final es 7,9004.
Evalúa.
Solución
Primero calcularemos la expresión en forma de agrupación
Para una expresión en forma de agrupación, recuerda siempre resolver el numerador antes que el denominador
A continuación, realizaremos la suma
Por último, realizaremos la resta
Así, la respuesta final es 3,8.
Evalúa .
Solución
Primero calcularemos la expresión dentro del paréntesis
A continuación, obtendremos el exponente
A continuación, realizaremos la división
Por último, sumaremos
Así, la respuesta final es 0,9025.
Operaciones con decimales - Puntos clave
- El orden de las operaciones con decimales obedece al PEMDAS: Paréntesis, Exponente, Multiplicación/División, Suma/Resta
- Pasos para sumar y restar decimales
Escribe los números en forma de columna. Asegúrate de que los decimales están alineados
Pon ceros para que los números tengan la misma longitud
Suma o resta utilizando la suma en columna o la resta en columna
- Pasos para multiplicar decimales
Quita los decimales y multiplica los números
Cuenta el número de decimales de cada número dado. Halla su suma
El valor posicional de la respuesta final es la suma de los decimales obtenidos en el Paso 2
- Pasos para dividir decimales
Convierte el divisor en un número entero multiplicándolo por una potencia de 10
Multiplica el dividendo por la misma potencia de 10 hallada en el Paso 1
Divide estos números utilizando la división larga
Al multiplicar decimales por potencias de 10, simplemente desplazamos el punto decimal hacia la derecha según el número de ceros de la potencia de 10.
Al dividir decimales por potencias de 10, basta con desplazar el punto decimal hacia la izquierda según el número de ceros de la potencia de 10.
Aprende con 16 tarjetas de Operaciones con decimales en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Operaciones con decimales
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
