Productos Notables: Binomios, Trinomios

Saltar a un capítulo clave

Un producto especial es un producto de dos binomios que siguen un patrón predecible.

Antes de sumergirnos en este tema, hagamos una rápida recapitulación sobre el método FOIL y su aplicación a la multiplicación de binomios.

Recapitulación sobre el método FOIL

Como hemos visto antes, podemos utilizar el método FOIL para multiplicar binomios. Ahora vamos a refrescar la memoria. La fórmula del método FOIL es la siguiente:

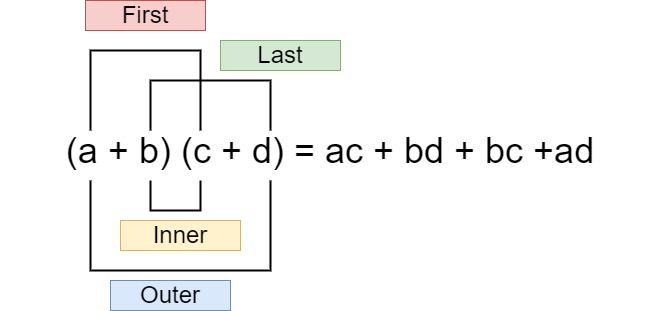
Considera ahora los siguientes ejemplos.

Utiliza el método FOIL para hallar los productos de las expresiones siguientes.

$\begin{array}{ll} 1 . (x - 1) (x + 1) & 2 . (2 x + 4) (2 x - 4) \\ 3 . {(3 x + 2)}^{2} & 4 . {(x + 9)}^{2} \\ 5 . {(x - 4)}^{2} & 6 . {(4 x - 5)}^{2} \end{array}$

¿Ves algún patrón cuando expandes estas expresiones?

Observa que en las Preguntas 1 y 2, el término medio desaparece cuando tenemos el producto de la suma y la diferencia de los dos términos. En las Preguntas 3, 4, 5 y 6, el término medio es el doble del producto de los términos del binomio.

Estos patrones son ejemplos de productos especiales. Este tipo de productos no requieren largos trabajos a la hora de resolverlos, ya que tienen reglas específicas que podemos seguir. ¡Los atajos de este tipo siempre son útiles! Utilizar productos especiales puede ayudarnos a expandir y factorizar polinomios de un modo más eficaz, reconociendo el patrón que tiene cada método. Éstos son nuestros objetivos de aprendizaje para este tema.

Identificar los patrones que se encuentran en los productos especiales
Utilizar estos patrones para expandir y factorizar polinomios
Resolver polinomios mediante estos métodos de factorización

En el siguiente segmento, veremos cada tipo de patrón por separado. Conoceremos tres tipos, a saber

Diferencia entre dos cuadrados
Trinomios cuadrados perfectos
Suma y diferencia de dos cubos

A partir de ahí, utilizaremos estos métodos para resolver polinomios como hicimos en el apartado anterior.

Fórmula de la suma y la diferencia

La fórmula general para la suma y la diferencia de dos términos es

$(a + b) (a - b) = a^{2} - b^{2}$ .

El patrón nos da la diferencia entre los dos cuadrados.

Representación geométrica

Ahora bien, la afirmación anterior puede parecer algo confusa. Para ayudarnos a entender lo que significa, intentemos visualizar este patrón geométricamente. Observa el cuadrado de abajo.

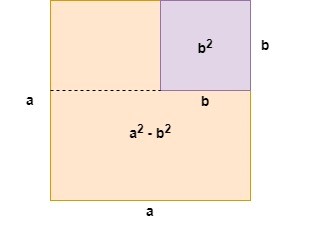
Aquí, el cuadrado grande tiene un área de $a^{2}$ y el cuadrado morado tiene un área de $b^{2}$ . Por tanto , el área de la región naranja es el área del cuadrado grande menos el área del cuadrado morado, $a^{2} - b^{2}$ . Hemos demostrado así el lado derecho de la fórmula de la suma y la diferencia.

Para mostrar el resultado del lado izquierdo, trazamos primero una línea horizontal discontinua como se muestra en el diagrama anterior. Esto crea un segmento que separa la región naranja en dos rectángulos. A continuación, desplazaremos este nuevo segmento hacia el lado izquierdo, como se muestra a continuación. Para verlo más claramente, este nuevo segmento se representa con el color rojo.

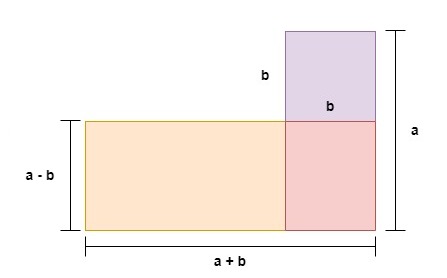
Ahora tenemos que hallar el área de la región naranja y el área de la región roja. Aquí vemos que la longitud horizontal de estas dos regiones es $a + b$ mientras que la longitud vertical es $a - b$ . Por tanto, el área combinada de los rectángulos naranja y rojo es $(a + b) (a - b)$ que satisface el lado izquierdo de la fórmula de la suma y la diferencia.

Ejemplos prácticos

Veamos los siguientes ejemplos prácticos.

Expande los siguientes términos.

$1 . (5 x + 4) (5 x - 4) 2 . (3 x + 7) (3 x - 7)$

Soluciones

1. Aquí, a = 5x y b = 4, por lo que

(5 x + 4) (5 x - 4) = {(5 x)}^{2} - {(4)}^{2} = 25 x^{2} - 16

2. Aquí, a = 3x y b = 7, por tanto

(3 x + 7) (3 x - 7) = {(3 x)}^{2} - {(7)}^{2} = 9 x^{2} - 49

Factoriza las siguientes expresiones.

$1 . x^{2} - 4 2 . 4 x^{2} - 36$

Soluciones

1. Puesto que

{(a)}^{2} = {(x)}^{2} = x^{2} a n d {(b)}^{2} = {(2)}^{2} = 4

Entonces

x^{2} - 4 = (x + 2) (x - 2)

2. Puesto que

{(a)}^{2} = {(2 x)}^{2} = 4 x^{2} a n d {(b)}^{2} = {(6)}^{2} = 36

Entonces

4 x^{2} - 36 = (2 x + 6) (2 x - 6)

Observa que no puedes factorizar la suma de dos cuadrados, es decir, ^a2 + ^b2. Puedes intentar hacerlo con el siguiente ejemplo: ^9x2 + 16. Observarás que es imposible factorizar esta expresión.

Por tanto, la diferencia entre dos cuadrados puede factorizarse como la suma y la diferencia de dos términos. Ahora, utilicemos este patrón para resolver polinomios. Para hallar las soluciones de un polinomio, pondremos la ecuación a cero y aplicaremos la Propiedad del Producto Cero, como vimos en la lección Factorización de polinomios.

Recuerda que la Propiedad del Producto Cero establece que si a x b = 0, entonces a = 0 o b = 0 (o ambos a = 0, b = 0).

Volveremos a los dos últimos ejemplos para demostrarlo.

Resuelve

$1 . x^{2} - 4 = (x + 2) (x - 2) = 0 2 . 4 x^{2} - 36 = (2 x + 6) (2 x - 6) = 0$

Soluciones

1. Hemos obtenido que $x + 2 = 0$ y $x - 2 = 0$ . Por tanto, tenemos dos raíces reales distintas:

x = - 2 a n d x = 2

2. Encontramos que $2 x + 6 = 0$ y $2 x - 6 = 0$ . Por tanto, tenemos dos raíces reales distintas:

x = - 3 a n d x = 3

Patrón del cuadrado de un binomio

El cuadrado de un binomio puede darse en dos casos

$C a s e 1 : {(a + b)}^{2} = a^{2} + 2 a b + b^{2} C a s e 2 : {(a - b)}^{2} = a^{2} - 2 a b + b^{2}$

En ambos casos, el término medio es el doble del producto de los términos del binomio. Sin embargo, en el caso 1, tenemos un término positivo, mientras que en el caso 2, tenemos un término negativo. Para estos casos, el patrón da un trinomio cuadrado perfecto.

Representación geométrica

¿Qué significa esto geométricamente hablando? Para mayor claridad, definamos los siguientes términos.

Un cuadrado perfecto es un número entero que es cuadrado de un número entero. Por ejemplo, $2^{2} = 4, 3^{2} = 9, 4^{2} = 16$ y así sucesivamente.

Un trinomio es un polinomio de tres términos.

Un binomio es un polinomio de dos términos.

Un trinomio cuadrado perfecto es un trinomio que puede escribirse como el cuadrado de un binomio, como en los dos casos anteriores.

Observa ahora el siguiente cuadrado.

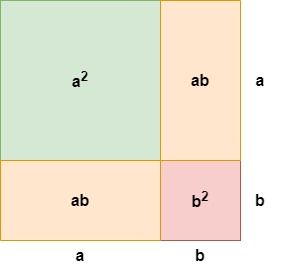
Observando el diagrama anterior, podemos ver que el cuadrado grande tiene un área de $(a + b) (a + b) = {(a + b)}^{2}$ . Está formado por el área de los cuadrados rojo y verde y el área de los dos rectángulos idénticos de color naranja. Sumándolos, obtenemos $a^{2} + a b + a b + b^{2} = a^{2} + 2 a b + b^{2}$ . Así, hemos deducido el primer caso.

El mismo concepto se sigue en el segundo caso. En este caso, sólo queremos el área del cuadrado verde y el área del cuadrado rojo, que es $a^{2} + b^{2}$ . Aquí, esencialmente estamos restando el área de los dos rectángulos naranjas idénticos del área de los cuadrados verde y rojo como $a^{2} - a b - a b + b^{2} = a^{2} - 2 a b + b^{2}$ . Factorizando el lado izquierdo de esta ecuación mediante agrupación, obtenemos

$a^{2} - a b - a b + b^{2} = a (a - b) - b (a - b) = (a - b) (a - b) = {(a - b)}^{2}$

como se requiere.

Ejemplos prácticos

Cuando factorices polinomios que puedan mostrar este patrón, recuerda comprobar el término medio para asegurarte de que cumple los criterios de los casos 1 ó 2. Aquí tienes algunos ejemplos prácticos de este patrón.

Expande los siguientes términos.

$1 . {(x + 2)}^{2} 2 . {(4 x - 3)}^{2}$

Soluciones

1. Aquí $a = x$ y $b = 2$ por tanto

{(x + 2)}^{2} = x^{2} + 2 (x) (2) + 2^{2} = x^{2} + 4 x + 4

2. aquí $a = 4 x$ y $b = 3$ por tanto

{(4 x - 3)}^{2} = {(4 x)}^{2} - 2 (4 x) (3) + 3^{2} = 16 x^{2} - 24 x + 9

Factoriza las siguientes expresiones.

$1 . x^{2} + 10 x + 25 2 . x^{2} - 14 x + 49$

Soluciones

1. Puesto que

{(a)}^{2} = {(x)}^{2} = x^{2} a n d {(b)}^{2} = {(5)}^{2} = 25

Así que

2 a b = 2 (x) (5) = 10 x

Por tanto

x^{2} + 10 x + 25 = {(x + 5)}^{2}

2. Puesto que

{(a)}^{2} = {(x)}^{2} = x^{2} a n d {(b)}^{2} = {(7)}^{2} = 49

Así que

2 a b = 2 (x) (7) = 14 x

por tanto,

x^{2} - 14 x + 49 = {(x - 7)}^{2}

Así, podemos factorizar un trinomio cuadrado perfecto por el cuadrado de un binomio. De nuevo, utilicemos este patrón para resolver algunos polinomios. Por simplicidad, volveremos a nuestros dos últimos ejemplos para demostrarlo.

Resuelve

$1 . x^{2} + 10 x + 25 = {(x + 5)}^{2} = 0 2 . x^{2} - 14 x + 49 = {(x - 7)}^{2} = 0$

Soluciones

1. Hemos obtenido que $x + 5 = 0$ . Por tanto, tenemos una solución que es una raíz real repetida:

$x = - 5$

2. Hemos obtenido que $x - 7 = 0$ . Por tanto, tenemos una solución que es una raíz real repetida:

x = 7

Suma y diferencia de dos cubos

Para factorizar la suma de dos cubos, podemos hacerlo aplicando la siguiente fórmula general:

$a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2})$ .

Aquí tienes algunos ejemplos prácticos para demostrarlo:

Factoriza las siguientes expresiones.

$1 . x^{3} + 125 2 . 8 x^{3} + 1$

Soluciones

1. Aquí

{(a)}^{3} = {(x)}^{3} = x^{3} a n d {(b)}^{3} = {(5)}^{3} = 125

Factorizando esto se obtiene

x^{3} + 125 = (x + 5) (x^{2} - (x) (5) + 5^{2}) = (x + 5) (x^{2} - 5 x + 25)

2. Aquí

{(a)}^{3} = {(2 x)}^{3} = 8 x^{3} a n d {(b)}^{3} = {(1)}^{3} = 1

Factorizando esto se obtiene

8 x^{3} + 1 = (2 x + 1) ({(2 x)}^{2} - (2 x) (1) + 1^{2}) = (2 x + 1) (4 x^{2} - 2 x + 1)

En cuanto a la factorización de la diferencia entre dos cubos, podemos utilizar la siguiente fórmula general:

$a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$ .

Veamos algunos ejemplos prácticos de este patrón:

Factoriza las siguientes expresiones.

$1 . 27 x^{3} - 8 2 . x^{3} - 64$

Soluciones

1. Aquí,

{(a)}^{3} = {(3 x)}^{3} = 27 x^{3} a n d {(b)}^{3} = {(2)}^{3} = 8

Por tanto, la forma factorizada es

27 x^{3} - 8 = (3 x - 2) ({(3 x)}^{2} + (3 x) (2) + 2^{2}) = (3 x - 2) (9 x^{2} + 6 x + 4)

2. Aquí

{(a)}^{3} = {(x)}^{3} = x^{3} a n d {(b)}^{3} = {(4)}^{3} = 64

Por tanto, la forma factorizada es

x^{3} - 64 = (x - 4) (x^{2} + (x) (4) + 4^{2}) = (x - 4) (x^{2} + 4 x + 16)

Consejo: Puede ser útil identificar los términos a y b antes de factorizar dichas expresiones para evitar confusiones.

Con esto, ya sabemos cómo factorizar la suma y la diferencia de dos cubos. Una vez más, intentaremos resolver polinomios utilizando este método. En este caso, observa que tenemos una expresión binómica y un trinomio cuadrático cuando factorizamos tanto la suma como la diferencia de cubos.

Determinar la solución a partir de la expresión binómica es, en efecto, sencillo. Sin embargo, no ocurre lo mismo con el trinomio cuadrático. Aquí, el trinomio cuadrático ya no se puede factorizar en productos de dos binomios, es decir, $(a + b) (c + d)$ . Por tanto, debemos utilizar la fórmula cuadrática para encontrar las dos soluciones restantes del polinomio.

Recapitula: La fórmula cuadrática

Para una ecuación cuadrática de la forma $a x^{2} + b x + c = 0$ donde a, b y c son coeficientes, la fórmula cuadrática es

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$ .

También es útil observar que las dos soluciones restantes sonsiempre un par de números complejos. Volveremos a nuestro último ejemplo para demostrarlo:

Recuerda que i = √-1 ya que ⁱ² = -1.

Resuelve

$x^{3} + 64 = = (x - 4) (x^{2} + 4 x + 16) = 0$

Solución

Tenemos que

x - 4 = 0 a n d x^{2} + 4 x + 16 = 0

Aquí tenemos una solución real, x = 4.

Adoptando la fórmula cuadrática, obtenemos las otras dos soluciones como

Aquí $a = 1, b = 4, c = 16$

x = \frac{- 4 \pm \sqrt{4^{2} - 4 (1) (16)}}{2 (1)} = \frac{- 4 \pm \sqrt{16 - 64}}{2} = \frac{- 4 \pm \sqrt{- 48}}{2} = \frac{- 4 \pm \sqrt{48} \sqrt{- 1}}{2} = \frac{- 4 \pm 4 i \sqrt{3}}{2} = - 2 \pm 2 i \sqrt{3}

Por tanto, tenemos un par de soluciones complejas

$x = - 2 - 2 i \sqrt{3} a n d x = - 2 + 2 i \sqrt{3}$

Productos especiales - Puntos clave

Los productos especiales nos permiten expandir expresiones sin utilizar el método FOIL.
Aplicar productos especiales nos permite factorizar polinomios de forma más eficaz.
La tabla siguiente resume las fórmulas importantes de los productos especiales. ¡Asegúrate de memorizarlas!

Tipo de factorización	Técnica
Diferencia de dos cuadrados	$(a + b) (a - b) = a^{2} - b^{2}$ Ten en cuenta que no puedes factorizar $a^{2} + b^{2}$
Trinomio cuadrado perfecto	${(a + b)}^{2} = a^{2} + 2 a b + b^{2} {(a - b)}^{2} = a^{2} - 2 a b + b^{2}$
Suma y diferencia de dos cubos	$a^{3} + b^{3} = (a + b) (a^{2} - a b + b^{2}) a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Productos Notables

¿Qué son los productos notables?

Los productos notables son fórmulas algebraicas que permiten simplificar y resolver ecuaciones de manera eficiente, como el cuadrado de la suma y el cubo de un binomio.

¿Cuál es la fórmula del cuadrado de un binomio?

La fórmula del cuadrado de un binomio es: (a + b)² = a² + 2ab + b².

¿Qué es la diferencia de cuadrados?

La diferencia de cuadrados es una fórmula notable que se expresa como: a² - b² = (a + b)(a - b).

¿Para qué se utilizan los productos notables?

Los productos notables se utilizan para simplificar la multiplicación de binomios y resolver ecuaciones algebraicas de manera más rápida y eficiente.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 11 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Productos Notables

Equipo editorial StudySmarter