Etiquetar un triángulo
Como vemos a continuación, siempre que rotulamos un triángulo, rotulamos los lados con minúsculas y los Ángulos con mayúsculas. Los ángulos y lados opuestos se etiquetan con la misma letra.
Ejemplo de triángulo etiquetado, Tom Maloy, StudySmarter Originals
La regla del seno
Para un triángulo con la forma anterior, la fórmula de la regla del seno se define como
También podemos escribirla como:
Podemos interpretar la regla del seno así: la Relación entre la longitud del lado y el ángulo opuesto es constante en cualquier triángulo. Utilizamos la regla del seno cuando intervienen dos ángulos y dos longitudes. Hay dos situaciones en las que utilizaremos la regla del seno:- Cuando hay dos ángulos y un lado dados, y necesitamos hallar la longitud de otro lado.
- Cuando hay dos longitudes y un ángulo dados, y necesitamos hallar otro ángulo.
Ejemplo 1
P: Halla x.
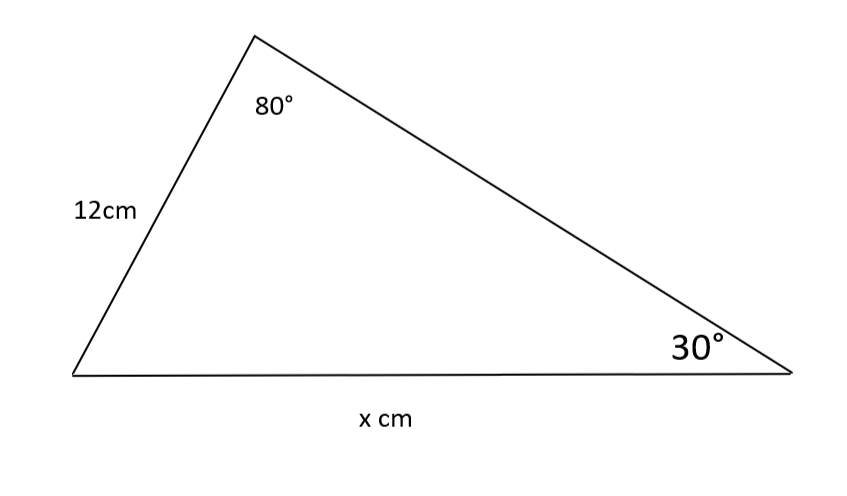
R: Usando la regla del seno, sabemos que y podemos reordenar x para obtener lo que da x = 23,6 (3 sf).
Ejemplo 2
P: Halla y.
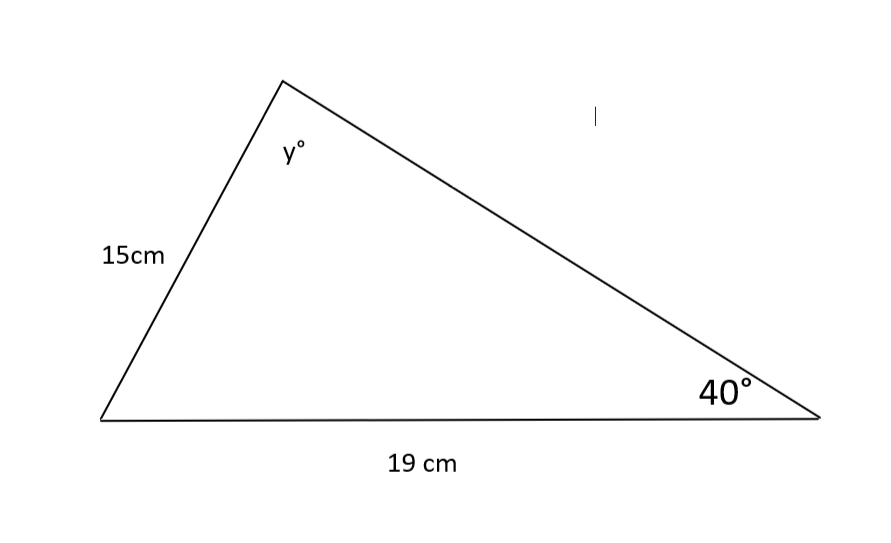
R: Utilizando la regla del seno, sabemos que que se reordena para dar dando y = = 54,5 ° (3.sf).
La regla del coseno
Utilizando el mismo ejemplo, la fórmula de la regla del coseno se define como: a² = b² + c²-2bc - cos (A)
Si reordenamos esto para dar A, obtenemos: Utilizamos la regla del coseno cuando intervienen tres longitudes y un ángulo. Las preguntas nos darán tres lados y tendremos que hallar un ángulo, o nos darán dos lados y un ángulo, y tendremos que hallar la longitud del lado.
Ejemplo 1
P: Halla x.
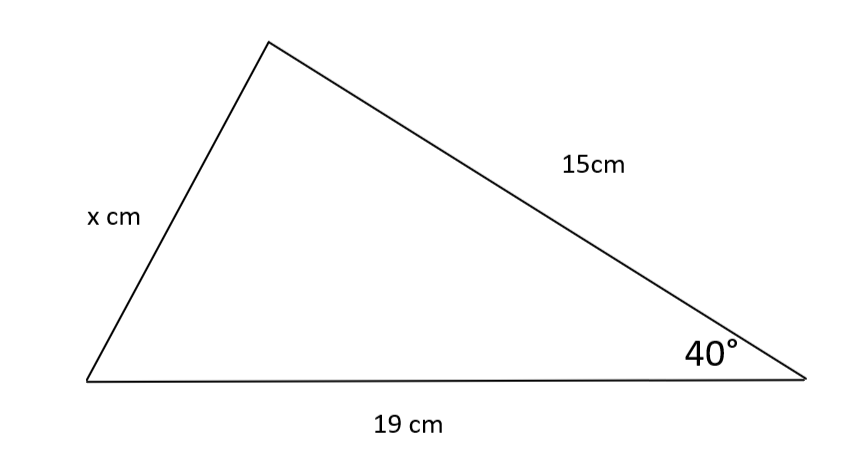
R: Utilizando la regla del coseno, obtenemos que x² = 15² + 19² -2 - 15 - 19 - cos (40) = 149,354667 ..., lo que da x = √149,354667 ... = 12,2 (3.sf)
Ejemplo 2
P: Halla y
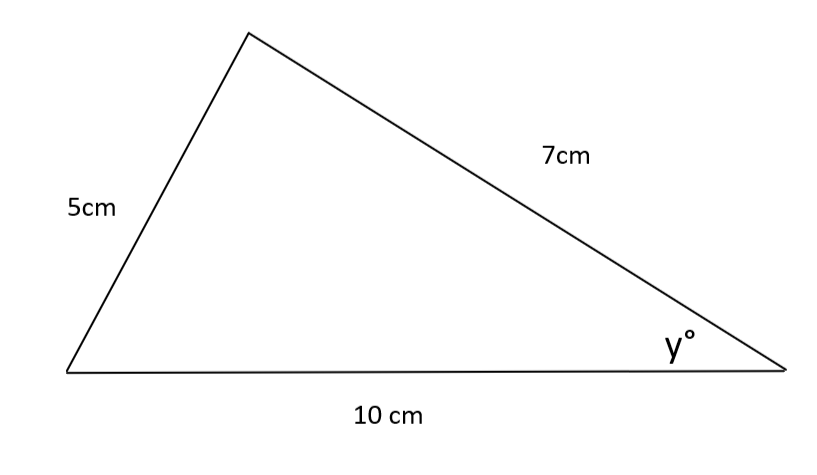
R: Utilizando la regla del coseno reordenada, obtenemos y = = 27,7 (3.sf)
¿Cómo se derivan las reglas del seno y del coseno?
Ahora que hemos visto qué es cada regla y cómo funcionan, veremos cómo llegamos a cada una de ellas derivándolas a partir de los primeros principios. Al principio pueden parecer complicadas, pero utilizaremos algo de trigonometría y el teorema de Pitágoras.
Derivación de la regla del seno
Empecemos con un triángulo como el anterior, pero tracemos una línea hacia abajo desde el ángulo superior, de modo que ahora tengamos dos triángulos rectángulos, y llamemos a esta línea h, como se muestra a continuación.
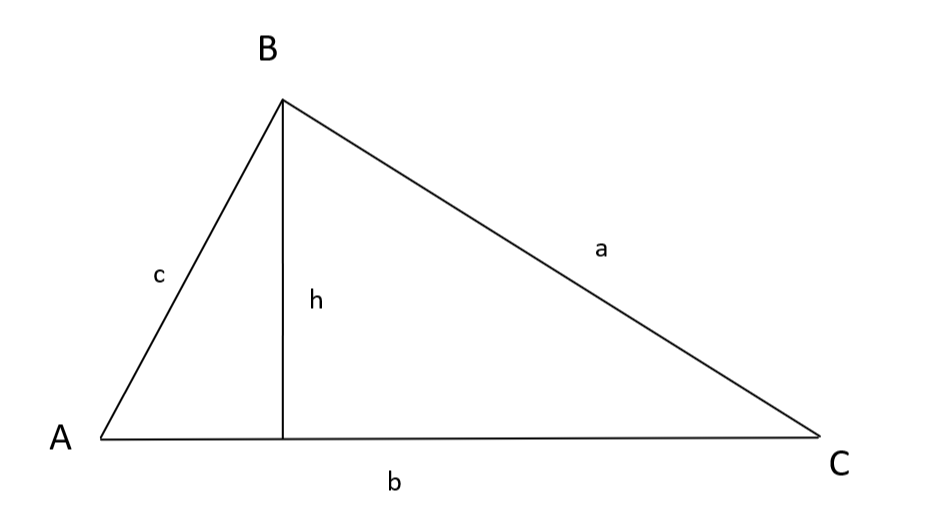
Utilizando la trigonometría, tenemos que sin (A) = h / c, y sin (C) = h / a. Ahora podemos reordenarlos para h y obtener h = c sin (A) y h = a sin (C). Hazlos iguales entre sí para obtener c sen (A) = a sen (C). Ahora se reordenan en o lo que es lo mismo . Podemos repetir este método con los otros dos ángulos para obtener los resultados. Así llegamos al resultado deseado de
Derivación de la regla del coseno
Ahora haremos lo mismo con la regla del coseno. Empezamos con el mismo triángulo, trazamos la misma recta hacia abajo para crear dos triángulos rectángulos, y llamamos a esta recta h. Llamamos D al punto que esta recta toca por abajo y afirmamos que un lado de la recta tiene longitud x, y el otro como se muestra a continuación.
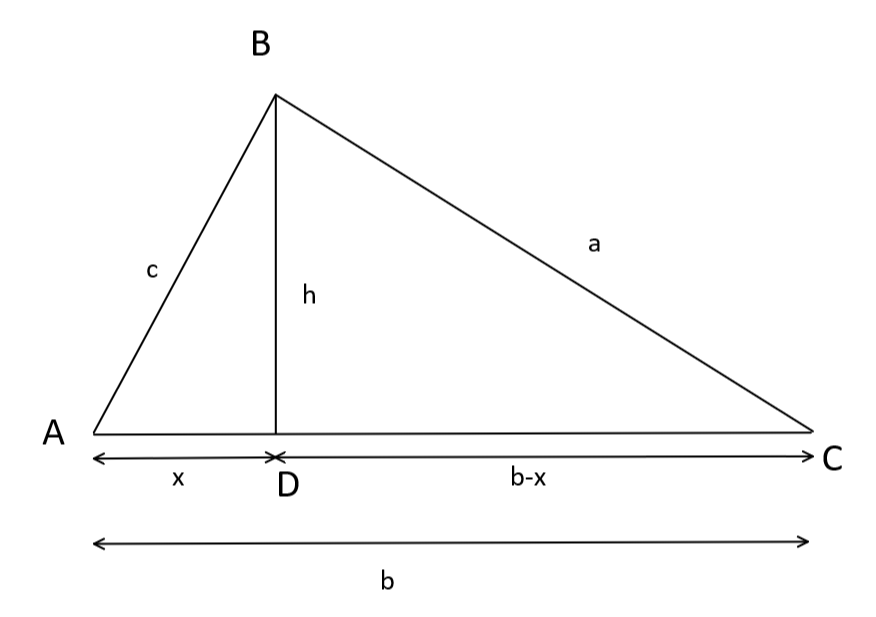
Por el teorema de Pitágoras sobre el triángulo de la izquierda, obtenemos x² + h² = c², y lo reordenaremos de la siguiente manera
x² = c²-h²......... (1) Haciendo lo mismo con el triángulo rectángulo, obtenemos y lo expandiremos a b²-2bx + x² + h² = a²....... ... (2) Si tomamos el coseno del ángulo A, obtenemos cos (A) = x / c, que se reordena a
..........(3). Ahora sustituiremos (1) y (3) en (2), utilizando (1) para deshacernos de la x², y (3) para sustituir la x en 2bx. Sustituyendo en: b² -2b (c - cos (A)) + c²-h² + h² = a². Podemos simplificarlo a a² = b² + c²-2bc - cos (A), que es nuestro resultado deseado.
Reglas del seno y el coseno - Puntos clave
- Utilizamos las reglas del seno y el coseno para calcular los lados y ángulos de triángulos no rectángulos.
- Usamos la regla del seno cuando tenemos un valor desconocido y tres valores conocidos de dos ángulos y dos lados.
- Usamos la regla del coseno cuando tenemos un valor desconocido y tres valores conocidos de un ángulo y tres lados.
- Tanto la regla del seno como la del coseno pueden deducirse de los primeros principios.
Aprende con 9 tarjetas de Reglas del Seno y del Coseno en la aplicación StudySmarter gratis
Tenemos 14,000 tarjetas de estudio sobre paisajes dinámicos.
¿Ya tienes una cuenta? Iniciar sesión
Preguntas frecuentes sobre Reglas del Seno y del Coseno
Acerca de StudySmarter
StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.
Aprende más
