Relación Multiplicativa

Halla las constantes de las relaciones multiplicativas siguientes.

1. 4 y 16
2. 2 y 6

Solución

a. 4 y 16

4 es la entrada y 16 es la salida. Puedes escribirlo en forma de ecuación de relación multiplicativa.

$$\begin{gathered} y=ax \\ 16=4a \end{gathered}$$

Dividiendo ambos lados de la ecuación por 4 para aislar $a$ obtenemos, $$\begin{gathered} \frac{16}{4}=\frac{4a}{4} \\ a=\frac{16}{4}=4 \end{gathered}$$

La constante es 4.

b. 2 y 6

2 es la entrada y 6 es la salida. Puedes escribir esto en forma de ecuación de relación multiplicativa para obtener la constante.

$$\begin{gathered} y=ax \\ 6=2a \end{gathered}$$

Dividiendo ambos lados de la ecuación por 2 para aislar $a$ obtenemos

$$\begin{gathered} \frac{6}{2}=\frac{2a}{2} \\ a=\frac{6}{2}=3 \end{gathered}$$

La constante es 3.

Determina qué conjunto de la tabla siguiente tiene una relación multiplicativa.

Veamos qué tendremos si los números del conjunto A se sustituyen en nuestra ecuación.

El primer par de números son 6 y 12. Nuestra ecuación sugiere que 6 multiplicado por un número dará 12. La sustitución en la ecuación da

$12=6a$

Simplifiquemos aún más para obtener la constante $a$,

$$\begin{gathered} 12=6a \\ \frac{12}{6}=\frac{6a}{6} \\ a=2 \end{gathered}$$

Ahora no podemos concluir que el conjunto A tiene una relación multiplicativa porque todavía hay otros pares de números que considerar y la constante $a$ tiene que ser la misma para todos ellos.

Los siguientes pares de números son 8 y 13. 13 es la salida $y$ y 8 es la entrada $x$. Sustituyamos la fórmula para ver qué constante $a$ sería.

$$\begin{gathered} y=ax \\ 13=8a \end{gathered}$$

Dividiendo ambos lados por 8 para aislar $a$obtenemos

$$\begin{gathered} \frac{13}{8}=\frac{8a}{8} \\ a=1.63 \end{gathered}$$

La constante que obtuvimos aquí es distinta de la que obtuvimos antes, lo que significa que los números del Conjunto A no tienen una relación multiplicativa.

Divide ambos lados por 3 para aislar $a$ para obtener

$$\begin{gathered} \frac{12}{3}=\frac{3a}{3} \\ a=4 \end{gathered}$$

La constante $a$ es 4. Veamos si será la misma para los demás números del conjunto.

El siguiente par de números son 5 y 20. Sustituyendo en la ecuación obtendremos,

$$\begin{gathered} y=ax \\ 20=5a \end{gathered}$$

La constante aquí es 4.

Muestra la relación multiplicativa entre los pares siguientes.

1. 15 y 17
2. 35 y 27

Solución

a. 15 y 17

Aquí, 15 es la entrada y 17 es la salida. Para mostrar la relación multiplicativa entre 15 y 17, tenemos que multiplicar 15 por una fracción. El numerador de la fracción debe ser 17 y el denominador debe ser 15, de modo que podamos cancelarlo para obtener 17 como respuesta.

Recordemos la ecuación de la relación multiplicativa.

$y=ax$

donde $y$ es 17

$x$ es 15

$a$ es la constante

$$\begin{gathered} y=15a \\ y=15\times \frac{17}{15} \\ y=\cancel{15}\times \frac{17}{\cancel{15}} \\ y=17 \end{gathered}$$

$y$ es 17 como se desee y $a$ es $\frac{17}{15}$.

b. 35 y 27

Aquí, 35 es la entrada y 27 es la salida. Para mostrar la relación multiplicativa entre 25 y 27, tenemos que multiplicar 35 por una fracción. El numerador de la fracción debe ser 27 y el denominador debe ser 35, de modo que podamos anular para obtener 27 como respuesta.

Recuerda, la ecuación de la relación multiplicativa.

$y=ax$

donde $y$ es 27

$x$ es 35

$a$ es la constante

$$\begin{gathered} y=35a \\ y=35\times \frac{27}{35} \\ y=\cancel{35}\times \frac{27}{\cancel{35}} \\ y=27 \end{gathered}$$

$yis27$ como se desea y $ais\frac{27}{35}$.

Determina qué conjunto de la tabla tiene una relación multiplicativa.

Solución

Queremos saber qué conjunto de números tiene una relación multiplicativa. Empecemos por el conjunto A.

El primer par de números del conjunto A son 3 y 7, donde 3 es la entrada y 7 la salida.

Recordemos la ecuación de la relación multiplicativa,

$y=ax$

Sustituiremos en la ecuación para obtener la constante,

$$\begin{gathered} 7=3a \\ \frac{7}{3}=\frac{3a}{3} \\ a=\frac{7}{3} \end{gathered}$$

La constante es $\frac{7}{3}$.

Averigüemos si el siguiente par dará la misma constante.

El siguiente par es 4 y 5, donde 4 es la entrada y 5 la salida.

Sustituyamos en la fórmula de la relación multiplicativa.

$$\begin{gathered} y=ax \\ 5=4a \\ \frac{5}{4}=\frac{4a}{4} \\ a=\frac{5}{4} \end{gathered}$$

Aquí la constante es distinta de la primera. Esto significa que los números del conjunto A no tienen relación multiplicativa.

Echemos un vistazo al conjunto B.

El primer par de números son 5 y 2, donde 5 es la entrada y 2 la salida.

Introduzcamos la fórmula de la relación multiplicativa.

$$\begin{gathered} y=ax \\ 2=5a \\ \frac{2}{5}=\frac{5a}{5} \\ a=\frac{2}{5} \end{gathered}$$

La constante es $\frac{2}{5}$. Si el resto del par tiene $\frac{2}{5}$ como constante, entonces existe una relación multiplicativa.

El siguiente par es 10 y 4, donde 10 es la entrada y 4 la salida.

Sustituyamos la fórmula de la relación multiplicativa.

$$\begin{gathered} y=ax \\ 4=10a \\ \frac{4}{10}=\frac{10a}{10} \\ a=\frac{4}{10}=\frac{2}{5} \end{gathered}$$

Tenemos una constante de $\frac{2}{5}$ que es la misma que la primera. Probemos con los dos últimos pares.

El tercer par es 20 y 8, donde 20 es la entrada y 8 la salida.

Sustituyendo en la fórmula obtendremos

$$\begin{gathered} y=ax \\ 8=20a \\ \frac{8}{20}=\frac{20a}{20} \\ a=\frac{8}{20}=\frac{2}{5} \end{gathered}$$

La constante es $\frac{2}{5}$ de nuevo.

El último par es 15 y 6, donde 15 es la entrada y 6 la salida.

Sustituyamos en la fórmula de la relación multiplicativa.

$$\begin{gathered} y=ax \\ 6=15a \\ \frac{6}{15}=\frac{15a}{15} \\ a=\frac{6}{15}=\frac{2}{5} \end{gathered}$$

De nuevo, tenemos que la constante es $\frac{2}{5}$. Esto significa que los números del conjunto B tienen una relación multiplicativa.

Si $y=4x$ completa la tabla siguiente y traza la gráfica.

Solución

La ecuación dada es $y=4x$ y observarás que tiene la forma de la ecuación de relación multiplicativa

$y=ax$

Lo que tenemos que hacer es sustituir los valores de $x$ en la ecuación dada para obtener $y$.

Cuando $x=0$,

$$\begin{gathered} y=4\times 0 \\ y=0 \end{gathered}$$

Cuando $x=1$,

$$\begin{gathered} y=4\times 1 \\ y=4 \end{gathered}$$

Cuando $x=2$,

$$\begin{gathered} y=4\times 2 \\ y=8 \end{gathered}$$

Cuando $x=3$,

$$\begin{gathered} y=4\times 3 \\ y=12 \end{gathered}$$

Ahora pongamos los resultados que hemos obtenido en la tabla.

Ahora que hemos completado la tabla, vamos a trazar la gráfica.

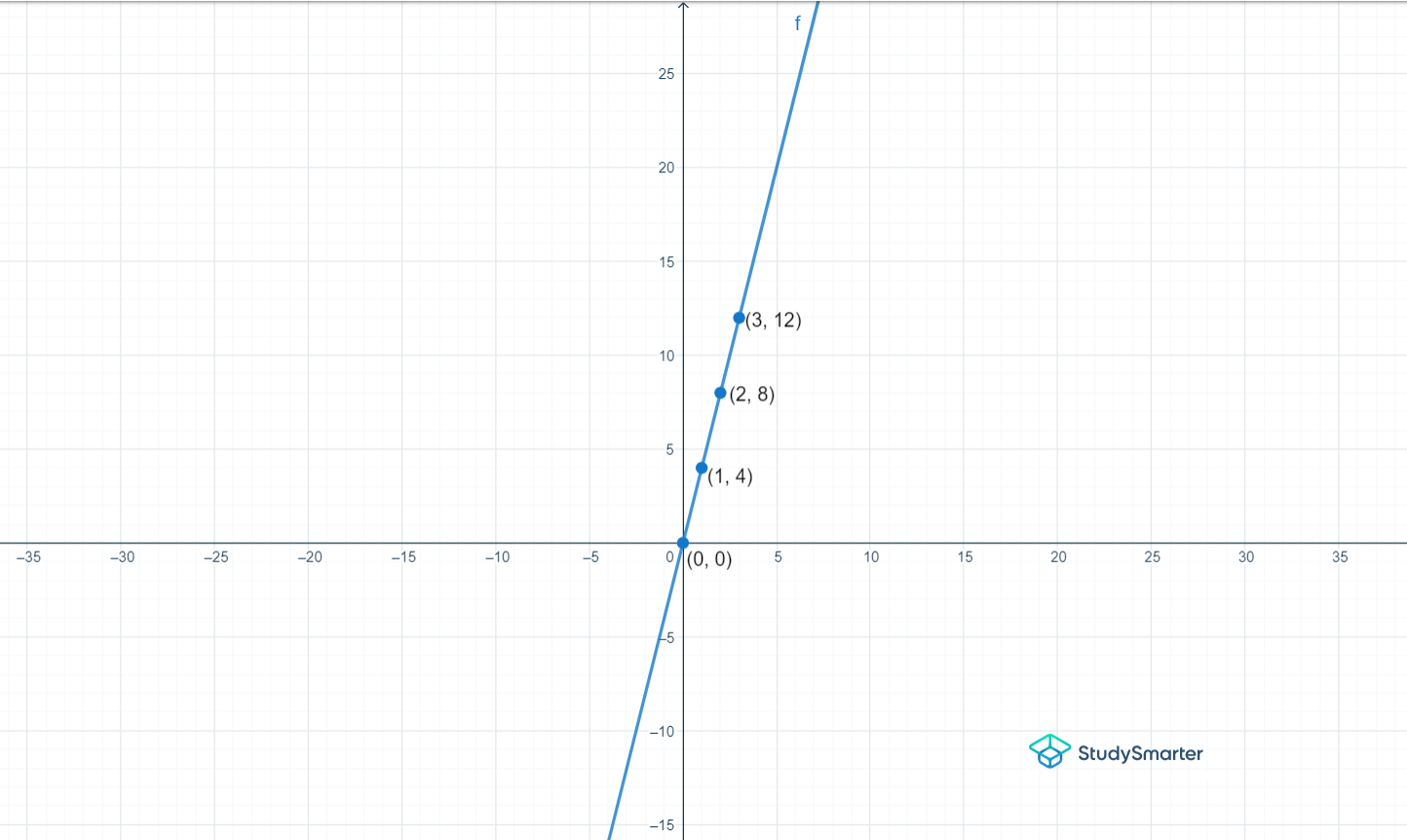
Podemos ver que la gráfica tiene las características de una gráfica de relación multiplicativa, es decir, es lineal y parte del origen (0, 0).

Una empresa paga a sus trabajadores 13€ por hora. Muestra aquí la relación multiplicativa, crea una tabla y traza un gráfico a partir de la información de la tabla.

Solución

La pregunta dice que una empresa paga 13 ¤ por hora. Lo creas o no, aquí hay que considerar dos cantidades. Hay que considerar el dinero ganado y las horas trabajadas.

Ahora, tenemos que averiguar qué son x e y.

Recuerda que x es la cantidad de entrada o independiente e y es la cantidad de salida o dependiente.

La cantidad independiente aquí son las horas trabajadas. Esto se debe a que el trabajador tiene control sobre ella. El trabajador decide cuántas horas puede trabajar. La cantidad dependiente es el dinero ganado, porque depende de cuántas horas se trabajen.

Recuerda la ecuación de la relación multiplicativa

$y=ax$

Un trabajador ganará 13€ por hora, lo que significa que $y=13$ y $x=1$. Podemos sustituir esto en la ecuación para obtener la constante,

$$\begin{gathered} y=ax \\ 13=1\times a \\ a=13 \end{gathered}$$

Para una pregunta como ésta, puede que no necesites dar este paso para hallar la constante, porque está bastante claro que tendrás que multiplicar 13 por el número de horas trabajadas para obtener el dinero total ganado.

Ahora pasemos a crear una tabla. La tabla contendrá el número de horas trabajadas y el dinero ganado. El número de horas se multiplicará por la constante 13 para obtener el dinero ganado.

Tenemos

$y=ax$

cuando $x=1$,

$$\begin{gathered} y=13\times 1 \\ y=13 \end{gathered}$$

cuando $x=2$,

$$\begin{gathered} y=13\times 2 \\ y=26 \end{gathered}$$

cuando $x=5$,

$$\begin{gathered} y=13\times 5 \\ y=65 \end{gathered}$$

cuando $x=6,$

$$\begin{gathered} y=13\times 6 \\ y=78 \end{gathered}$$

Por tanto, utilizaremos los valores que tenemos para rellenar la tabla.

Con esta información, ahora podemos trazar una gráfica.

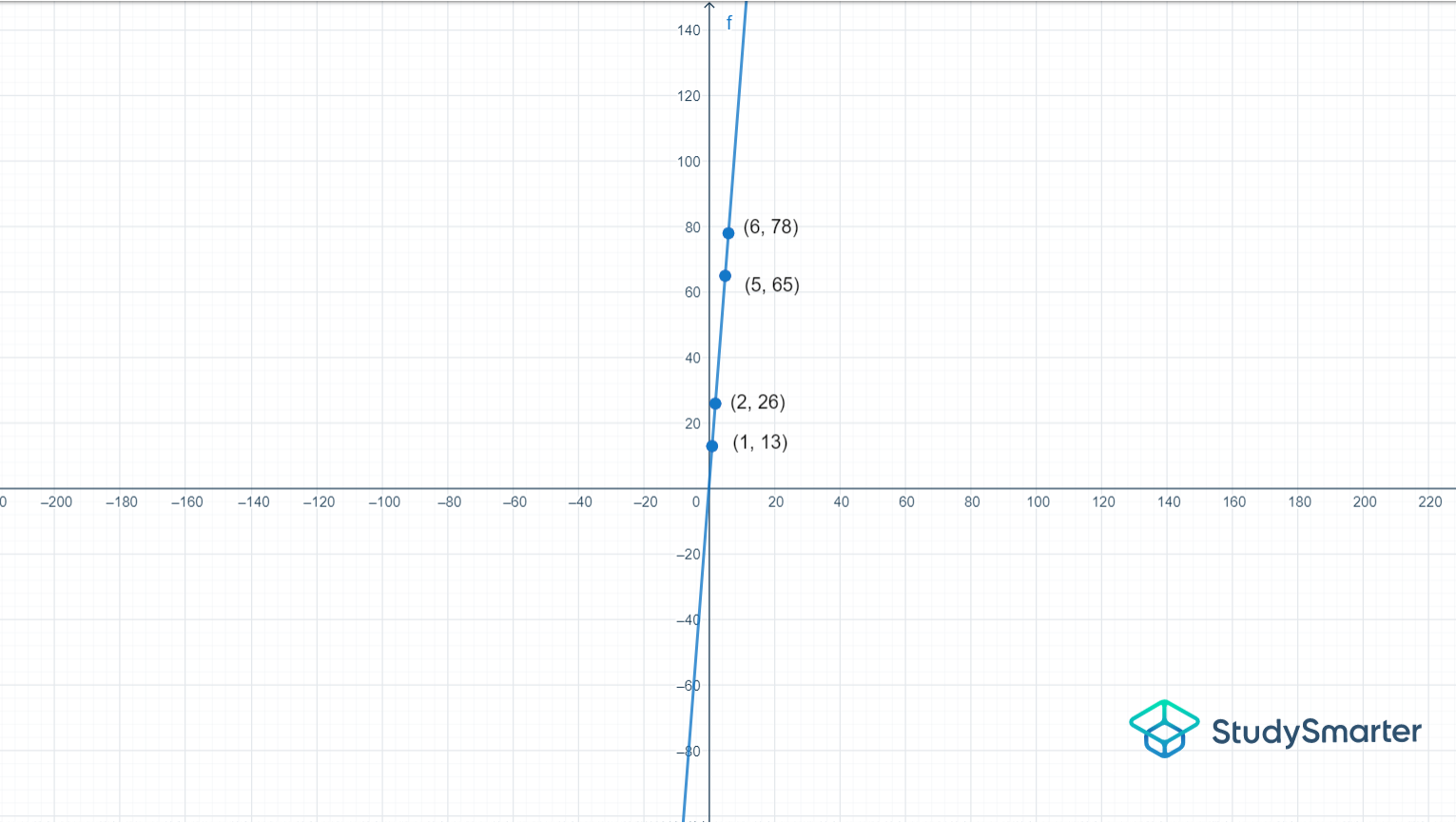
Sabemos que la gráfica es correcta porque es lineal.