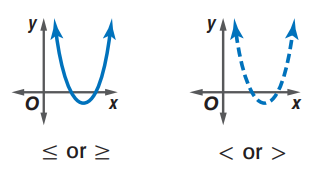Desigualdades Cuadráticas
Antes de empezar, definamos una desigualdad cuadrática.
Una desigualdad cuadrática es un polinomio de segundo grado que utiliza un signo de desigualdad en lugar de un signo igual.
Hay cuatro tipos de desigualdades cuadráticas (en dos variables) que trataremos en este tema, a saber
Una desigualdad cuadrática en una variable sólo tiene una incógnita en la expresión cuadrática y puede representarse en un único eje o recta numérica, que suele ser el eje x. La gráfica de una desigualdad cuadrática en dos variables está formada por todos los pares ordenados (x, y) que son soluciones de la desigualdad cuadrática dada.
Una inecuación cuadrática en dos variables describe una región en el plano cartesiano con una parábola (curva) como límite. Aquí consideramos tanto el eje x como el eje y.
Las formas estándar de las inecuaciones cuadráticas (en una variable) son:
Resolución de desigualdades cuadráticas en una variable
Resolver inecuaciones cuadráticas en una variable es esencialmente similar a resolver ecuaciones cuadráticas. La única diferencia aquí es que nos interesa encontrar el intervalo de números reales para el que se satisface la desigualdad, en lugar de igualar a cero la expresión dada.
En este apartado, utilizaremos métodos básicos de factorización para resolver dichas desigualdades cuadráticas. A continuación se explican los pasos de esta técnica.
Paso1: Escribe la inecuación cuadrática en forma general, es decir, con ax2 + bx + c, donde a ≠ 0, en un lado de la inecuación;
Paso2: Factoriza completamente la expresión cuadrática de la desigualdad;
Paso3: Identifica las raíces de la desigualdad, mediante la ecuación correspondiente;
Paso4 : Determina el comportamiento de la desigualdad cuadrática:
Si la desigualdad es de la forma cuando entonces ;
Si la desigualdad es de la forma cuando entonces .
Paso 5: Expresa la solución en notación de desigualdades o en notación de intervalos
Los casos a) y b) son similares para las desigualdades < y > respectivamente.
Graficar desigualdades cuadráticas en una variable
Para evaluar desigualdades cuadráticas en una variable, también podemos utilizar la gráfica del polinomio dado. La tabla siguiente describe la representación gráfica para cada caso de desigualdad que puede tener la cuadrática.
La región sombreada en los gráficos de abajo representa la solución correcta de la desigualdad cuadrática dada
| Caso | a > 0 | a < 0 |
| 1 | ax2 + bx + c < 0 |
Método:- Gráfica y = ax2 + bx + c
- Como y es negativa, determina los valores de x para los que la gráfica está por debajo del eje x
- Para >, no incluyas los intersticios x en la solución. Esto se indica mediante círculos abiertos (como se ve en la gráfica)
- Escribe la solución en términos de su notación de intervalo (como se muestra debajo de cada gráfica)
| 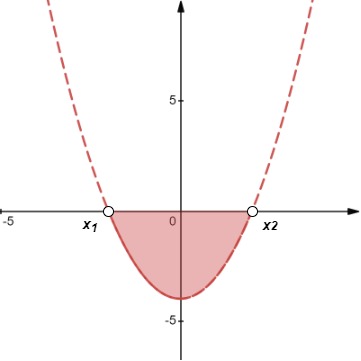
Gráfica de la desigualdad Caso 1 (a), Aishah Amri - StudySmarter Originals Solución: x1 < x < x2 | 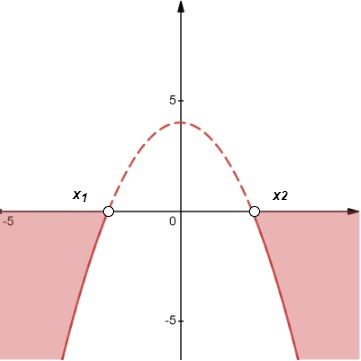
Gráfico de la desigualdad Caso 1 (b), Aishah Amri - StudySmarter Originals Solución:x < x1 o x > x2 |
| 2 | ax2 + bx + c ≥ 0 |
Método: - Gráfica y = ax2 + bx + c
- Como y es positiva, determina los valores de x para los que la gráfica está por encima del eje x
- Para ≤, incluye los intersticios x en la solución. Esto se indica mediante círculos cerrados (como se ve en la gráfica)
- Escribe la solución en términos de su notación de intervalo (como se muestra debajo de cada gráfica)
| 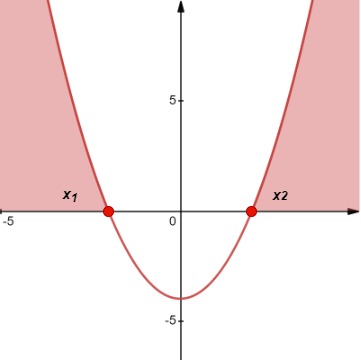
Gráfico de la desigualdad Caso 2 (a), Aishah Amri - StudySmarter Originals Solución:x ≤ x1 o x ≥ x2 | 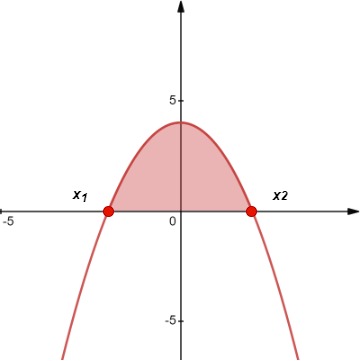
Gráfico de desigualdad Caso 2 (b), Aishah Amri - StudySmarter Originals Solución: x1 ≤ x ≤ x2 |
Resuelve la desigualdad .
Solución
Paso 1: Llevando -6 al lado izquierdo de la desigualdad, obtenemos
Factorizando esta desigualdad cuadrática obtenemos
Paso2: Ahora necesitamos encontrar las raíces de la desigualdad. Nuestro primer instinto aquí puede ser utilizar la Propiedad del Producto Cero. Sin embargo, ten en cuenta que la Propiedad del Producto Cero se utiliza para ecuaciones, no para desigualdades. En lugar de eso, tenemos que resolver las intersecciones x cambiando la desigualdad por una ecuación y ajustando el signo de la desigualdad a la situación actual en función de las intersecciones x encontradas. Esto se muestra a continuación.
Paso3: A partir de la tabla, vemos que esta desigualdad obedece al Caso 2 con a > 0. Como y es positiva, debemos elegir los valores de x para los que la curva está por encima del eje x.
Paso 4: Ahora, escribiendo la solución en notación de intervalo, obtenemos
La gráfica se muestra a continuación.
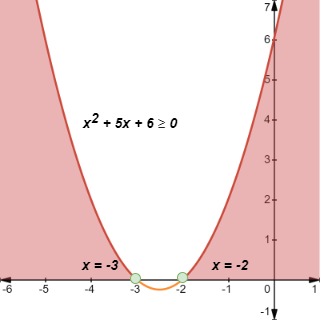
Ejemplo 1, Aishah Amri - StudySmarter Originals
Resuelve la desigualdad .
Solución
Paso 1: Llevando 19x y -6 al lado izquierdo de la desigualdad, obtenemos
Factorizando esta desigualdad cuadrática obtenemos
Paso 2: Al igual que en el ejemplo anterior, trataremos nuestra desigualdad anterior como una ecuación para determinar sus raíces como se indica a continuación.
Paso3: Consultando de nuevo nuestra tabla, vemos que esta desigualdad obedece al Caso 1 con a > 0. Como y es negativa, debemos elegir los valores de x para los que la curva está por debajo del eje x.
Paso 4: Así, escribiendo la solución en su correspondiente forma de notación interválica, tenemos
La gráfica se muestra a continuación.
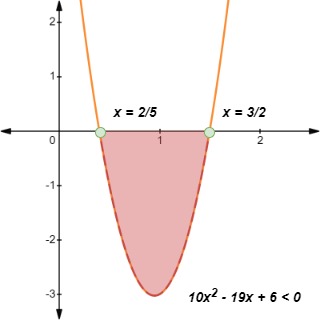
Ejemplo 2, Aishah Amri - StudySmarter Originals
Graficación de inecuaciones cuadráticas en dos variables
La representación gráfica de desigualdades cuadráticas (en dos variables) utiliza los mismos principios que la representación gráfica de desigualdades lineales. A continuación encontrarás un método detallado para resolver estos problemas.
Paso 1: Dibuja la función cuadrática y = ax2 + bx + c. Determina la naturaleza de la parábola basándote en la desigualdad dada.
Dibuja una parábola discontinua para las inecuaciones con < o > para describir que los puntos de la parábola no son soluciones.
Dibuja una parábola sólida para las desigualdades con ≤ o ≥ para describir que los puntos de la parábola son soluciones.
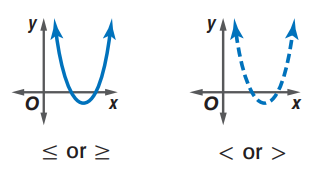
Glencoe McGraw-Hill, Álgebra 2 (2008)
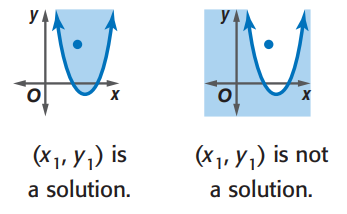
Paso 2: Toma un punto (x1, y1) dentro de la parábola. Comprueba si este punto es una solución de la desigualdad.
Glencoe McGraw-Hill, Álgebra 2 (2008)
Paso 3: Sombrea la región correcta que satisfaga la desigualdad.
Si (x1, y1) es una solución, sombrea la región dentro de la parábola.
Si (x1, y1) no es una solución, sombrea la región fuera de la parábola.
Glencoe McGraw-Hill, Álgebra 2 (2008)
A continuación encontrarás varios ejemplos prácticos para demostrar esta técnica.
Grafica la desigualdad cuadrática .
Solución
Paso 1: Empezamos graficando el polinomio
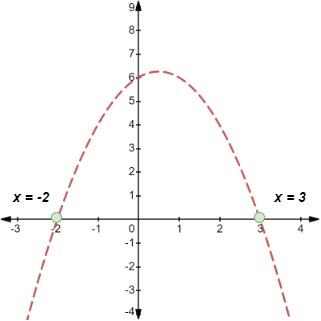
El coeficiente de x2 es negativo, por lo que la curva se abre hacia abajo. Factorizando esta expresión, obtenemos
Igualando a cero, tenemos raíces en .
Como la desigualdad es >, nuestra curva debe ser una línea discontinua. La gráfica se muestra a continuación.
Ejemplo 3 (1), Aishah Amri - StudySmarter Originals
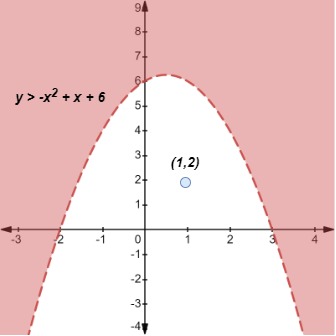
Paso 2: Probemos ahora un punto dentro de la parábola, digamos (1, 2). Introduciendo x = 1 e y = 2 en nuestra desigualdad cuadrática, encontramos que
Paso3: 2 no es mayor que 6, por lo que la desigualdad falla. Por tanto, (1, 2) no es una solución de la desigualdad y debemos sombrear la región exterior a la parábola, como se muestra a continuación.
Ejemplo 3 (2), Aishah Amri - StudySmarter Originals
Ahora, si consideramos la desigualdad cuadrática en una variable, obtenemos
Por tanto, y es negativa y debemos elegir los valores de x para los que la curva está por debajo del eje x. La gráfica final se muestra a continuación.
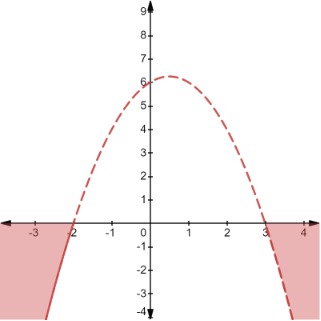
Ejemplo 3 (3), Aishah Amri - StudySmarter Originals
Utilizar la fórmula cuadrática para resolver inecuaciones cuadráticas
Al igual que para resolver ecuaciones cuadráticas que no pueden factorizarse mediante técnicas de factorización estándar, podemos aplicar la Fórmula Cuadrática para evaluar desigualdades cuadráticas.
Grafica la desigualdad cuadrática .
Solución
Paso 1: Como antes, intentaremos primero representar gráficamente el polinomio .
El coeficiente de x2 es positivo, por lo que la curva se abre. Observa que no podemos factorizar esta expresión utilizando los métodos de factorización estándar. Por tanto, aplicaremos la Fórmula Cuadrática para determinar las raíces.
Dado que
evaluamos
Así, obtenemos dos raíces irracionales
Como la desigualdad es ≤, nuestra curva debe ser una recta continua. La gráfica se muestra a continuación.
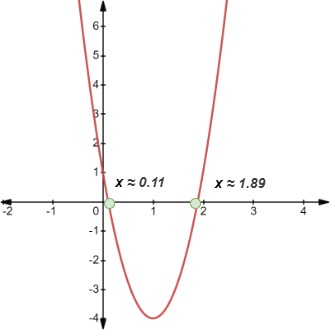
Ejemplo 4 (1), Aishah Amri - StudySmarter Originals
Paso 2: Comprobemos ahora un punto dentro de la parábola, digamos (1, -1). Introduciendo x = 1 e y = -1 en nuestra desigualdad, encontramos que
Paso3: -1 no es menor ni igual que -4, por lo que la desigualdad falla. Por tanto, (1, -1) no es una solución de la desigualdad y debemos sombrear la región exterior a la parábola como se indica a continuación.
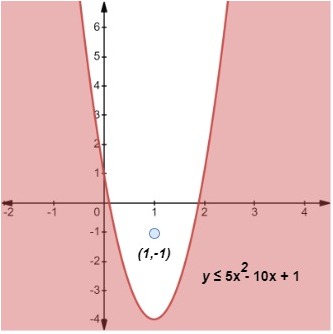
Ejemplo 4 (2), Aishah Amri - StudySmarter Originals
Ahora, si consideramos la desigualdad cuadrática en una variable, obtenemos
Por tanto, y es positiva y debemos elegir los valores de x para los que la curva está por encima del eje x. La gráfica final se muestra a continuación.
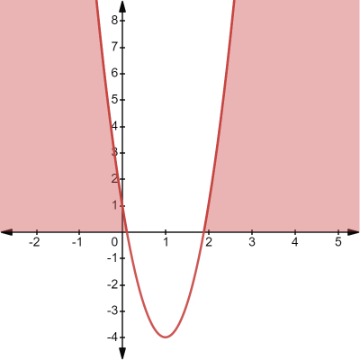
Ejemplo 4 (3), Aishah Amri - StudySmarter Originals
Ejemplos reales con desigualdades cuadráticas
Las desigualdades cuadráticas pueden ayudar a modelizar ciertos tipos de situaciones del mundo real, como las finanzas, el movimiento y la arquitectura. He aquí un ejemplo que muestra cómo podemos aplicar las desigualdades cuadráticas en esos casos.
La altura de una pelota lanzada entre dos personas puede modelizarse mediante la función
,
donde la altura h viene dada en metros y el tiempo x en segundos. ¿En qué momento de su vuelo está la pelota a menos de 6 metros del suelo?
Solución
La altura de la pelota se describe mediante la función h.
Queremos encontrar los valores de x para los que h(x) ≤ 6.
Haciendo la gráfica de la función y = -7x2 + 15x - 4, obtenemos el siguiente esquema.
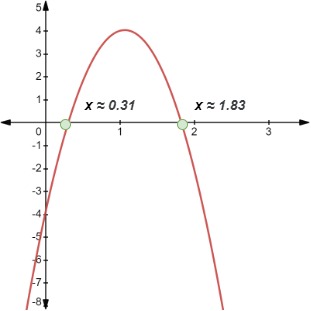
Ejemplo 5 (1), Aishah Amri - StudySmarter Originals
Las raíces pueden hallarse utilizando la Fórmula Cuadrática, ya que la expresión -7x2 + 15x - 4 no puede factorizarse más utilizando métodos de factorización estándar. Al hacerlo, obtuvimos las dos raíces siguientes, correctas con dos decimales: x ≈ 0,31 y x ≈ 1,83.
Considerando ahora la desigualdad, la región para la que se satisface la expresión se muestra a continuación.
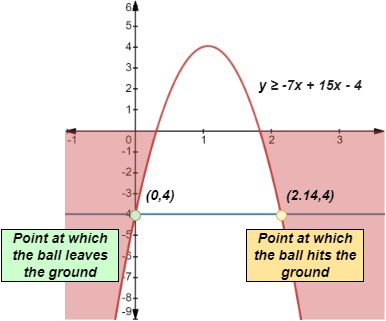
Ejemplo 5 (2), Aishah Amri - StudySmarter Originals
Observa que la gráfica está por debajo del eje x cuando x < 0,31 o x > 1,83. De aquí concluimos que la pelota está a menos de 6 metros del suelo durante los primeros 0,31 segundos de su vuelo y de nuevo después de 1,83 segundos hasta que la pelota toca el suelo a los 2,14 segundos.
Graficar y resolver desigualdades cuadráticas - Puntos clave
- La gráfica de una desigualdad cuadrática está formada por todos los pares ordenados (x, y) que son soluciones de la desigualdad cuadrática dada.
- Resolución de inecuaciones cuadráticas en una variable
- Escribe la desigualdad cuadrática en forma general: ax2 + bx + c, donde a ≠ 0
- Factoriza completamente la expresión cuadrática de la desigualdad
- Identificalas raíces de la desigualdad
- Expresa la solución en notación de desigualdades o en notación de intervalos
- Determina el comportamiento de la desigualdad cuadrática
- Para las desigualdades < o >, la parábola es una línea discontinua. Esto demuestra que los puntos de la parábola no son soluciones.
- Para las desigualdades ≤ o ≥, la parábola es continua. Esto demuestra que los puntos de la parábola son soluciones.
- Gráfica de las desigualdades cuadráticas en dos variables
- Dibuja la función cuadrática y = ax2 + bx + c. Determina la naturaleza de la parábola a partir de la desigualdad dada.
- Toma un punto (x1, y1) dentro de la parábola. Comprueba si este punto es una solución de la desigualdad.
- Sombrea la región correcta que satisfaga la desigualdad.
- Para ax2+ bx + c < 0, identifica los valores de x para los que la gráfica está por debajo del eje x (ya que y es negativa).
- La solución es x1 < x < x2
- Para ax2+ bx + c > 0 identifica los valores x para los que la gráfica está por encima del eje x (ya que y es positiva)
- La solución es x < x1 o x > x2