Tipos de Triángulos: Ángulos, Lados

Saltar a un capítulo clave

Las clasificaciones detriángulos definen los triángulos por sus propiedades geométricas. Estas clasificaciones son: equilátero, isósceles, rectángulo y escaleno.

Sin embargo, antes de empezar a clasificar triángulos, primero debemos discutir cuáles son exactamente esas propiedades que definen la clasificación de un triángulo dado.

Tipos de propiedades de los triángulos

Como ya hemos dicho, los triángulos se clasifican por sus propiedades geométricas. Las dos propiedades geométricas por las que se clasifican los triángulos son las longitudes de los lados y los ángulos interiores.

Como puede verse en el diagrama siguiente, los ángulos interiores del triángulo son los ángulos cerrados formados por cada par de lados del triángulo. Estos ángulos se denotan por $α$ , $β$ y $γ$ (letras griegas minúsculas).

Se cumple en todos los triángulos que sus ángulos interiores suman $180 ° .$

Cada lado del triángulo tiene una longitud, indicada por $a$ , $b$ y $c .$ Las longitudes individuales de estos lados no determinan la clasificación del triángulo, de hecho, pueden tener cualquier longitud. En realidad, lo importante es la longitud de los lados entre sí.

Clasificaciones de triángulos, ángulos de triángulos, longitudes de lados de triángulos. StudySmarter

Un triángulo destacando sus ángulos interiores y las longitudes de sus lados, StudySmarter Originals

Con estas dos propiedades geométricas, es posible colocar cualquier triángulo en una de nuestras cuatro clasificaciones, y en muchos casos, ¡sólo necesitamos una u otra!

Definiciones de los tipos de triángulos

Como ya hemos dicho, los cuatro tipos de triángulos son equiláteros,isósceles, escalenos y rectángulos. Cada uno de ellos es un triángulo con el que te habrás encontrado antes, ¡pero quizá no lo sabías! Veamos qué es cada uno de ellos.

Triángulos equiláteros

La clasificación más sencilla de un triángulo es el triángulo equilátero . El nombre de este triángulo indica cómo se define. Equi es un prefijo común que procede del adjetivo igual, por lo que las palabras que empiezan con este prefijo suelen describir cosas que son iguales. Por ejemplo, si dos tiendas están equidistantes de donde te encuentras, significa que cada una está a la misma distancia. Los triángulos equiláteros no son diferentes.

Un triángulo equil átero es un triángulo con tres lados de igual longitud. En consecuencia, los ángulos interiores de un triángulo equilátero también son iguales entre sí.

El triángulo que se muestra a continuación es un triángulo equilátero, lo que se aprecia inmediatamente por los guiones simples de cada lado, que significan que los lados tienen la misma longitud, es decir, $a = b = c$ . También se puede ver que los ángulos interiores del triángulo son iguales, siendo cada uno de ellos $60 °$ , pero ¿es siempre así?

Clasificaciones de los triángulos, ángulos de los triángulos, longitudes de los lados de los triángulos. triángulo equilátero, tipos de triángulo StudySmarter Un triángulo equilátero, caracterizado por sus tres lados iguales y sus tres ángulos interiores iguales, StudySmarter Originals

Como sabemos, los ángulos interiores de un triángulo suman siempre $180 ° .$ Digamos que cada ángulo del triángulo equilátero es $α .$

$180 ° = 3 \times α$

Dividiendo ambos lados por tres podemos hallar el valor de $α .$

$α = 60 °$

Así que ya lo tenemos, los ángulos interiores de un triángulo equilátero son siempre cada uno de ellos $60 °!$

Triángulos isósceles

El siguiente tipo de triángulo que vamos a estudiar es el triángulo isósceles. Al igual que los triángulos equiláteros, podemos reconocer un triángulo isósceles por la longitud de sus lados o por el tamaño de sus ángulos interiores.

Un triángulo is ósceles es un triángulo con dos lados de igual longitud y un tercero de longitud diferente. En consecuencia, sólo dos de los ángulos interiores de un triángulo isósceles son iguales.

El triángulo de abajo es un triángulo isósceles. En este caso, los guiones indican que sólo los lados $a$ y $b$ son iguales. Los ángulos interiores $β$ y $γ$ son iguales, pero no el ángulo $α .$

Clasificaciones del triángulo, ángulos del triángulo, longitud del lado del triángulo, triángulo isósceles, tipos de triángulo StudySmarter Un triángulo isósceles, caracterizado por tener dos lados y dos ángulos iguales, StudySmarter Originals

Triángulos escalenos

Ya hemos visto los triángulos equiláteros, que tienen tres lados iguales, y los triángulos isósceles, que tienen dos lados iguales, así que ¿cuál será el caso de los triángulos escalenos? Lo has adivinado, ¡no tienen lados iguales!

Un triángulo escaleno es un triángulo sin lados de igual longitud. En consecuencia, ninguno de los ángulos interiores es igual.

El triángulo de abajo es un triángulo escaleno. Como tal, no tiene guiones que indiquen lados iguales.

Clasificaciones de triángulos, ángulos de triángulos, longitud lateral de triángulos, triángulo escaleno, tipos de triángulos StudySmarter Un triángulo escaleno, caracterizado por no tener lados ni ángulos interiores iguales, StudySmarter Originals

Triángulos rectángulos

El último tipo de triángulo es el triángulo rectángulo. A diferencia de los tipos de triángulos anteriores, los triángulos rectángulos no se definen por el número de lados iguales ni por el número de ángulos iguales. De hecho, lo único que debe poseer un triángulo para ser rectángulo es un ángulo interior igual a $90 ° .$ En otras palabras, debe poseer un ángulo recto. Esto significa que un triángulo rectángulo será también un triángulo isósceles o un triángulo escaleno.

Un triángulo rect ángulo es un triángulo que posee un ángulo interior de $90 ° .$ Sus otros dos ángulos interiores pueden ser iguales o no iguales, y puede tener dos o cero lados iguales.

El triángulo de abajo es un triángulo rectángulo. Se reconoce inmediatamente por el recuadro en lugar del segmento angular habitual, que denota un $90 °$ ángulo.

Clasificaciones de triángulos, ángulos de triángulos, longitud lateral de triángulos, triángulo rectángulo, tipos de triángulos StudySmarter Un triángulo rectángulo, caracterizado por tener un único ángulo interior recto, StudySmarter Originals

Los triángulos rectángulos son extremadamente importantes en matemáticas, ¡por qué no te diriges a nuestras explicaciones sobre el Teorema de Pitágoras y la Trigonometría para aprender realmente lo que los hace especiales!

Ejemplos de tipos de triángulos

Veamos ahora si podemos utilizar lo que hemos aprendido para intentar clasificar algunos triángulos.

¿A qué clasificación de triángulos pertenece cada uno de los triángulos siguientes?

Encontrar el tipo de un triángulo, clasificaciones de triángulos, triángulo isósceles studysmarter Triángulo de la pregunta a) con tres ángulos marcados, StudySmarter Originals

Solución:

Este triángulo es un triángulo isósceles , ya que tiene dos ángulos iguales, $β$ y $γ,$ y un tercero que no lo es.

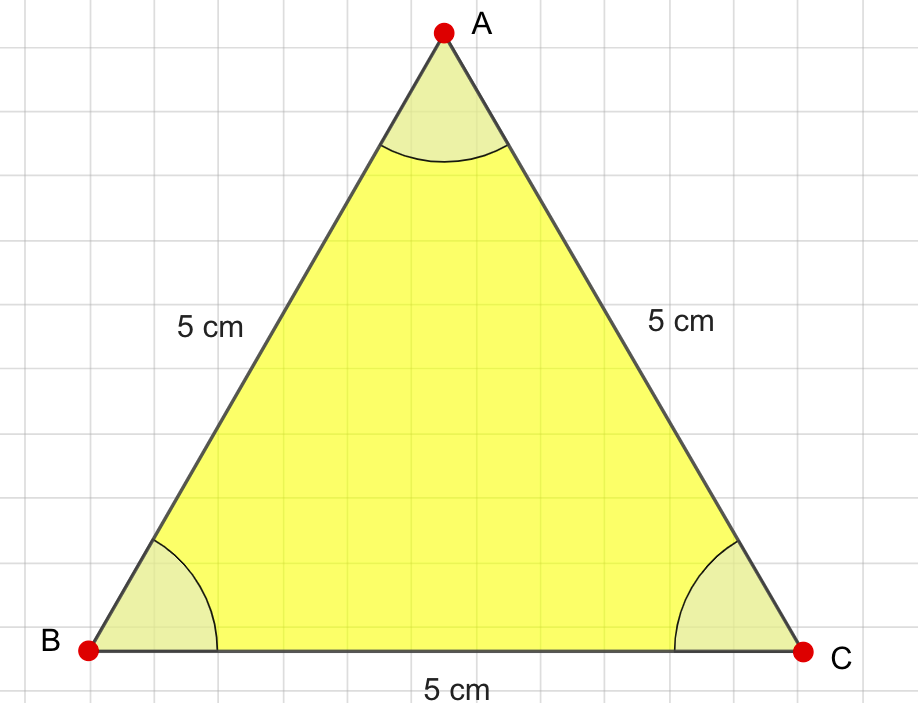
Encontrar el tipo de un triángulo, clasificaciones de triángulos, triángulo equilátero studysmarter

Triángulo de la pregunta b) con tres lados marcados, StudySmarter Originals

Solución:

Este triángulo es un triángulo equilátero , ya que tiene tres lados de igual longitud.

Encontrar el tipo de triángulo, clasificaciones de triángulos, triángulo rectángulo studysmarter Triángulo para la pregunta c), con dos ángulos etiquetados, StudySmarter Originals

Solución:

Sólo se nos dan dos ángulos para este triángulo; sin embargo, sabiendo que los ángulos interiores de un triángulo siempre suman $180 °,$ podemos determinar el tercer ángulo, $γ .$ En primer lugar, igualamos la suma de los tres ángulos a $180 ° .$

$180 ° = α + β + γ$

A continuación, sustituimos los ángulos que conocemos y reordenamos la ecuación para hallar $γ .$

$180 ° = 64 ° + 26 ° + γ$

$γ = 180 ° - 64 ° - 26 °$

$γ = 90 °$

Como el tercer ángulo $γ,$ es un ángulo recto, el triángulo es un triángulo rectángulo. Como los tres ángulos interiores son distintos, también es un triángulo escaleno.

Encontrar el tipo de un triángulo, clasificaciones de triángulos, triángulo escaleno studysmarter Triángulo para la pregunta d), con tres ángulos etiquetados, StudySmarter

Solución:

Este triángulo es un triángulo escaleno, ya que ninguno de sus ángulos interiores es igual.

Encontrar el tipo de un triángulo, clasificaciones de triángulos, triángulo isósceles studysmarter

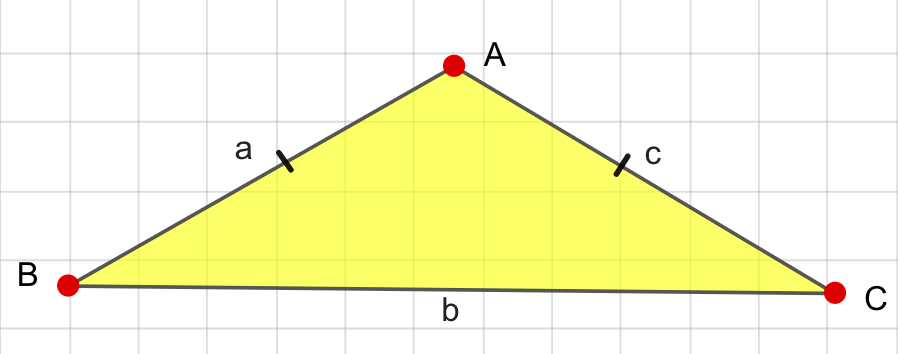
Triángulo para la pregunta e), sin ángulos ni lados etiquetados, StudySmarter Originals

Solución:

El triángulo es un triángulo isósceles, ya que tiene dos lados de la misma longitud, indicados por los dos guiones.

Encontrar el tipo de un triángulo, clasificaciones de triángulos, triángulo rectángulo studysmarter Triángulo de la pregunta f), con dos ángulos marcados, StudySmarter

Solución:

En esta pregunta se nos dan dos ángulos interiores que son iguales. Recordando que todos los ángulos interiores de un triángulo suman $180 °,$ podemos utilizar estos dos ángulos interiores para hallar el tercer ángulo, $γ .$

En primer lugar, igualamos los tres ángulos interiores a $180 ° .$

$180 ° = α + β + γ$

Luego, sustituimos los ángulos que conocemos y reordenamos la ecuación para hallar $γ .$

$180 ° = 45 ° + 45 ° + γ$

$γ = 180 ° - 45 ° - 45 °$

$γ = 90 °$

Como el triángulo tiene un ángulo interior recto y dos ángulos interiores iguales, debe ser a la vez un triánguloisósceles y un triángulo rectángulo .

Tipos de triángulos - Puntos clave

Los triángulos pueden clasificarse comparando la longitud de sus lados y el tamaño de sus ángulos interiores.
Hay cuatro tipos de triángulos: equiláteros, isósceles, escalenos y rectángulos.
Los triángulos equiláteros tienen tres lados iguales y tres ángulos interiores iguales.
Los triángulos isósceles tienen dos lados iguales y dos ángulos interiores iguales.
Los triángulos escalenos no tienen lados iguales ni ángulos interiores iguales.
Los triángulos rectángulos tienen un ángulo interior de $90 ° .$

Aprende con 0 tarjetas de Tipos de Triángulos en la aplicación StudySmarter gratis

Regístrate con email

¿Ya tienes una cuenta? Iniciar sesión

Preguntas frecuentes sobre Tipos de Triángulos

¿Cuáles son los tipos de triángulos?

Los tipos de triángulos son equilátero, isósceles y escaleno, según sus lados, y acutángulo, rectángulo y obtusángulo, según sus ángulos.

¿Qué es un triángulo isósceles?

Un triángulo isósceles tiene dos lados de igual longitud y un lado diferente.

¿Cómo se distingue un triángulo escaleno?

Un triángulo escaleno tiene todos sus lados de diferente longitud.

¿Qué características tiene un triángulo equilátero?

Un triángulo equilátero tiene los tres lados de igual longitud y todos sus ángulos son de 60 grados.

Guardar explicación

Descubre materiales de aprendizaje con la aplicación gratuita StudySmarter

Regístrate gratis

Acerca de StudySmarter

StudySmarter es una compañía de tecnología educativa reconocida a nivel mundial, que ofrece una plataforma de aprendizaje integral diseñada para estudiantes de todas las edades y niveles educativos. Nuestra plataforma proporciona apoyo en el aprendizaje para una amplia gama de asignaturas, incluidas las STEM, Ciencias Sociales e Idiomas, y también ayuda a los estudiantes a dominar con éxito diversos exámenes y pruebas en todo el mundo, como GCSE, A Level, SAT, ACT, Abitur y más. Ofrecemos una extensa biblioteca de materiales de aprendizaje, incluidas tarjetas didácticas interactivas, soluciones completas de libros de texto y explicaciones detalladas. La tecnología avanzada y las herramientas que proporcionamos ayudan a los estudiantes a crear sus propios materiales de aprendizaje. El contenido de StudySmarter no solo es verificado por expertos, sino que también se actualiza regularmente para garantizar su precisión y relevancia.

Aprende más

Equipo editorial StudySmarter

Equipo de profesores de Matemáticas

Tiempo de lectura de 9 minutos
Revisado por el equipo editorial de StudySmarter

Guardar explicación

Tipos de Triángulos

Equipo editorial StudySmarter

Tipos de propiedades de los triángulos