Ahora bien, ¿qué ocurriría si rociaras dos ambientadores distintos al mismo tiempo en el mismo lugar general? Aunque los olores se mezclarán, uno se olerá antes en el extremo opuesto de la habitación que el otro. ¿A qué se debe esto? Pues la ley de Graham tiene la respuesta, ¡sigue leyendo para averiguarlo!
- Este artículo trata sobre la ley de Graham .
- En primer lugar, definiremos la ley de Graham.
- A continuación, veremos la ecuación de la ley de Graham.
- Luego veremos las dos partes de la ley de Graham: La ley de Graham de la difusión y la ley de Graham de la efusión.
- Por último, trabajaremos con algunos ejemplos utilizando la ley de Graham.
Definición de la ley de Graham
Empecemos por ver la definición de la ley de Graham.
Laley de Graham afirma que la velocidad de difusión o efusión de un gas es inversamente proporcional a la raíz cuadrada de las masas molares de sus partículas.
Ladifusión es el proceso por el que las partículas se desplazan de una zona de alta densidad a otra de baja densidad
Laefusión es el proceso de escape de partículas de gas de su recipiente a otro recipiente a través de un pequeño orificio. El diámetro de este agujero es mucho menor que la trayectoria libre media de la partícula, que es la distancia que recorre una partícula antes de chocar con algo. Esencialmente, esto significa que sólo una partícula puede atravesar el agujero a la vez.
Ahora bien, ésta es una definición un poco complicada. Para ayudarnos, vamos a ver primero la ecuación.
Ecuación de la Ley de Graham
La ecuación de la ley de Graham es:$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}$$
Donde
- MAy TasaAson la masa molar y la tasa de efusión/difusión del gas, A respectivamente.
- MBy TasaBson la masa molar y la tasa de efusión/difusión del gas, B, respectivamente.
Lo que esto nos dice básicamente es la relación de las tasas en función de sus masas. En términos más sencillos, cuanto más pesado sea el gas, más despacio irá. He aquí un ejemplo:
Calcula la velocidad de efusión/difusión de un recipiente con gas helio (He) y gas neón (Ne).
La masa molar del helio es de 4,00 g/mol, y la masa molar del neón es de 20,2 g/mol. Introduciendo esto, obtenemos
$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{\frac{M_{Ne}}{M_{He}}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{\frac{20.2\frac{g}{mol}}{4.00\frac{g}{mol}}}$$
$$\frac{Rate_{He}}{Rate_{Ne}}=\sqrt{5.05}$$
$$\frac{Rate_{He}}{Rate_{Ne}} =2.25$$
Esto significa que el helio se fundirá/difundirá 2,25 veces más rápido que el neón.
Para comprender mejor este concepto, dividamos esta ley en dos partes: difusión y efusión.
Ley de difusión de Graham
Hablemos primero un poco más de lo que es la difusión. Como hemos dicho en la introducción, cuando rocías un ambientador, el aerosol sólo se olerá en la zona directa, pero las partículas acabarán esparciéndose por la habitación.
Aquí tienes un diagrama de lo que ocurre:
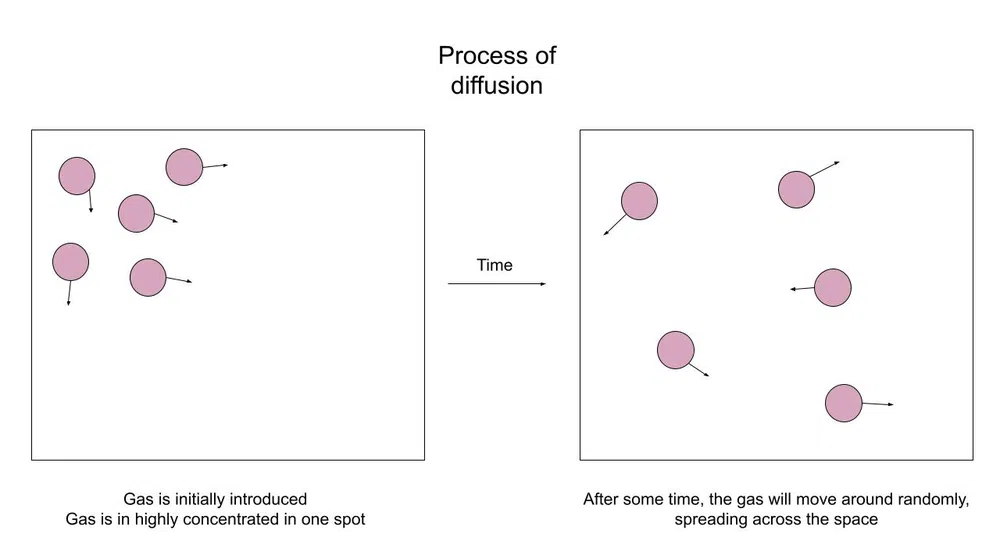
Fig.1-Las partículas se difunden por un espacio
El objetivo de la difusión es crear un equilibrio. El equilibrio es esencialmente un estado de equilibrio. En este caso, equilibrio significa una concentración equilibrada en todo el recipiente.
Entonces, ¿qué ocurre cuando hay dos gases? Ahí es donde entran en juego los pasos de la ley de Graham.
Nuestro supuesto principal es que ambos gases están a la misma temperatura y, por tanto, tienen la misma energía cinética, que es la energía del movimiento.
De hecho, de ahí procede la ley de Graham. Ésta es la fórmula de la energía cinética
$$KE=\frac{1}{2}*M_A*\nu_{rms}^2$$
Donde KE es la energía cinética,MA es la masa molar de la especie A y νrms es la velocidad media cuadrática.
La velocidad media cuadrática (velocidad RMS) es la velocidad media de un gas. La fórmula es
$$\nu_{rms}=\sqrt{3RTM}$$
Donde R es la constante de los gases ideales, T es la temperatura y M es la masa molar del gas.
En realidad no necesitas preocuparte por la definición exacta de la velocidad RMS, así que por ahora puedes pensar en ella como "velocidad".
Para los gases, no utilizamos la velocidad normal, ya que la velocidad neta de un gas es cero, puesto que los gases se moverán en todas las direcciones (es decir, se anularán entre sí, ya que la velocidad es velocidad + dirección)
Siguiendo con nuestra derivación, vamos a igualar las energías cinéticas de nuestros dos gases (A y B):
$$KE=\frac{1}{2}*M_A*\nu_{rms,A}^2=\frac{1}{2}*M_B*\nu_{rms,B}^2$$
A continuación, podemos anular el 1/2, ya que está en ambos lados:
$$M_A*\nu_{rms,A}^2=M_B*\nu{rms,B}^2$$
A continuación, trasladamos nuestros dos términos de masa molar a un lado y nuestros términos de velocidad RMS al otro:
$$\frac{M_A}{M_B}=\frac{\nu_rms,B^2}{\nu_rms,A^2}$$
Por último, sacamos la raíz cuadrada de ambos lados:
$$\sqrt\frac{M_A}{M_B}=\frac{\nu_rms,B}{\nu_rms,A}$$
Ahora que sabemos cómo hemos obtenido nuestra ecuación, veámosla en acción.Anteriormente, calculamos que el helio se difundiría 2,25 veces más rápido que el neón, a continuación se muestra un diagrama que muestra este proceso:
 Fig.2-Experimento de la ley de difusión de Graham.
Fig.2-Experimento de la ley de difusión de Graham.
Esencialmente, el helio se va a difundir más rápidamente, ya que es más ligero. Esto significa que llegarán más partículas de helio al "lado" del neón.
Piénsalo como hacer rodar una pelota de ping-pong frente a una de fútbol. Si hago rodar ambas pelotas con exactamente la misma cantidad de energía, la pelota de ping-pong viajará más lejos (es decir, tendrá mayor velocidad) que la pelota de fútbol, ya que la pelota de ping-pong es mucho más ligera.
Sin embargo, al cabo de cierto tiempo, habrá un equilibrio de gases, es decir, la misma concentración en ambos lados.
La ley de Graham de la efusión
Hablemos ahora de la efusión .
Como recordatorio, aquí tienes la definición de efusión de antes:
Laefusión es el proceso de escape de partículas de gas de su recipiente a otro recipiente a través de un pequeño orificio. El diámetro de este orificio es mucho menor que la trayectoria libre media de la partícula, que es la distancia que recorre una partícula antes de chocar con algo. Esencialmente, esto significa que sólo una partícula puede viajar a la vez a través del agujero.
Esencialmente, la efusión es lo mismo que la difusión, salvo que las partículas pasan a través de un agujero en lugar de moverse por un espacio abierto.Este es el aspecto de este proceso:
 Fig.3 Efusión gaseosa
Fig.3 Efusión gaseosa
Al igual que ocurre con la difusión, durante la efusión los gases se desplazan hacia una zona menos concentrada. Veamos ahora cómo es la efusión con dos gases según la ley de Graham:
 Fig.4-Ley de Graham de efusión para el helio y el neón
Fig.4-Ley de Graham de efusión para el helio y el neón
Los dos globos están conectados por un pequeño orificio, que suponemos sellado (es decir, ningún gas puede escapar aparte del intercambio entre los dos globos). Como el helio se mueve más deprisa, efundirá a mayor velocidad que el neón. Esto significa que el globo de neón se inflará a medida que el helio se efunda, mientras que el globo de helio se desinfla, ya que está perdiendo ese helio.
Ejemplos de la Ley de Graham
Ahora que comprendemos mejor el concepto de efusión y difusión, ¡vamos a trabajar con algunos ejemplos!
Una muestra de gas nitrógeno y oxígeno está en un recipiente con un pequeño orificio que da a otro recipiente vacío. ¿Cuál de los gases se derramará primero?
- La masa molar del nitrógeno es de 14,00 g/mol y la del oxígeno es de 16,00 g/mol.
Aunque podemos introducir esto en nuestra ecuación, en realidad sólo tenemos que fijarnos en las masas molares. El nitrógeno es más ligero, por lo que se derramará más rápido y, por tanto, primero.
Ahora hagamos un ejemplo en el que realmente calculemos algo:
¿Cuál es la relación entre la velocidad de difusión del gas cloro (Cl2) y la del gas criptón (Kr)?
- La masa molar del cloro es de 35,45 g/mol y la masa molar del criptón es de 83,80 g/mol.
Como el cloro gaseoso es Cl2 y no Cl, tenemos que duplicar el valor de la masa molar cuando lo introduzcamos en nuestra ecuación:
$$\frac{Rate_A}{Rate_B}=\sqrt{\frac{M_B}{M_A}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{M_{Kr}}{M_{Cl2}}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{83.80\frac{g}{mol}}{(35.45\frac{g}{mol}*2)}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{\frac{83.80\frac{g}{mol}}{70.9\frac{g}{mol}}}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=\sqrt{1.18}$$
$$\frac{Rate_{Cl2}}{Rate_{Kr}}=1.09$$
Como el cloro gaseoso y el criptón gaseoso tienen una masa similar, la diferencia en la velocidad de difusión no es tan grande. Cuanto mayor sea la diferencia de masa, mayor será la relación de velocidades.
Ley de Graham - Puntos clave











